深度学习模型训练计算量的估算
- 方法1:基于网络架构和批处理数量计算算术运算次数
- 前向传递计算和常见层的参数数量
- 全连接层(Fully connected layer)
- 参数
- 浮点数计算量
- CNN
- 参数
- 浮点数计算量
- 转置CNN
- 参数
- 浮点数计算量
- RNN
- 参数
- 浮点数计算量
- GRU
- 参数
- 浮点数计算量
- LSTM
- 参数
- 浮点数计算量
- Self-Attention
- 参数
- 浮点数计算量
- Multi-Headed Attention
- 参数
- 浮点数计算量
- 示例:CNN-LSTM-FCN模型
- 方法2:基于硬件设置和训练时间计算运算次数
- 1.从论文/参考文献中提取信息:
- 2.阅读硬件规格
- 3.进行估算
- 估算GPU的总FLOP:
- 精度的考虑:
- 考虑硬件特性:
深度学习模型训练计算量的估算
在当今的机器学习领域,深度学习模型的性能和先进性往往与其在更多计算资源上进行的训练有关。为了确保不同深度学习模型之间的准确比较,估算和报告训练过程中的计算资源使用情况变得至关重要。
本文将探讨深度学习模型训练计算量的估算方法,并介绍了该领域的一些前沿。
计算资源的使用通常以训练模型的最终版本所需的浮点运算次数(FLOP)来衡量。
我们将重点介绍两种估算方法,以大家更好地理解和比较不同深度学习模型的训练计算量,这两种方法用于估算深度学习模型的训练计算量:
- 一种基于网络架构和批处理数量
- 一种基于硬件的最大配置和模型训练时间
方法1:基于网络架构和批处理数量计算算术运算次数
这种方法通过分析模型的架构和训练数据量来估算计算量。我们将探讨如何通过这种信息来估算模型训练的计算资源需求,以及其在实际研究中的应用。
大致公式如下:
计算量 = 2 × c o n n e c t i o n s × 3 × t r a i n i n g e x a m p l e × e p o c h s 计算量 = 2 \times connections \times 3 \times training \space example \times epochs 计算量=2×connections×3×training example×epochs
connections:指的是神经网络中的连接数,即神经元之间的直接相互连接。在神经网络中,神经元之间的连接表示它们之间的信息传递和相互作用。
举个例子,如果你有一个具有 N 个输入神经元和 M 个输出神经元的全连接层(fully connected layer),那么它将有 NM 个连接。这意味着每个输入神经元都与每个输出神经元相连接,形成了 NM 个连接。
training example:指的是用于训练机器学习模型的数据集中的样本数量
epochs:是指在训练深度学习模型时的迭代次数
计算资源的使用通常是以模型的前向传播(inference)或反向传播(backpropagation)所需的浮点运算次数(FLOP)来衡量。这是在单次迭代(一个batch)中的计算,而不是迭代的总和,在深度学习框架中,每个批次计算完成后,框架通常会自动释放相应的计算资源,包括中间结果的内存。
为什么不可以层层计算,释放资源,进入下一层呢?
在神经网络的训练中,每一层的计算都依赖于前一层的输出,因此不能在每一层的计算中释放资源并进入下一层。神经网络的计算通常是流水线式的,每一层的输出是下一层的输入。如果在每一层都等待上一层计算完成并释放资源,会导致整个计算过程变得非常慢。
下面我们可以将上面的公式翻译转换一下,可以用如下公式来解释:
t r a i n i n g _ c o m p u t e = ( o p s _ p e r _ f o r w a r d _ p a s s + o p s _ p e r _ b a c k w a r d _ p a s s ) ∗ n _ p a s s e s training\_compute = (ops\_per\_forward\_pass + ops\_per\_backward\_pass) * n\_passes training_compute=(ops_per_forward_pass+ops_per_backward_pass)∗n_passes
其中:
- ops_per_forward_pass:表示的是前向传播中的计算数
- ops_per_backward_pass:是反向传播中的计算数
- n_passes:等于模型迭代次数和训练样本数的乘积:
n _ p a s s e s = n _ e p o c h s ∗ n _ e x a m p l e s n\_passes = n\_epochs * n\_examples n_passes=n_epochs∗n_examples
如果不知道自己一个迭代的训练样本数,有时可以计算为每个迭代的批次数乘以每个批次的大小
n _ e x a m p l e s = n _ b a t c h e s ∗ b a t c h _ s i z e n\_examples = n\_batches * batch\_size n_examples=n_batches∗batch_size
ops_per_backward_pass与ops_per_forward_pass的比率相对稳定,因此可以将二者整合为
f p _ t o _ b p _ r a t i o = o p s _ p e r _ b a c k w a r d _ p a s s o p s _ p e r _ f o r w a r d _ p a s s fp\_to\_bp\_ratio = \frac{ops\_per\_backward\_pass}{ops\_per\_forward\_pass} fp_to_bp_ratio=ops_per_forward_passops_per_backward_pass。
得到以下公式:
t r a i n i n g _ c o m p u t e = o p s _ p e r _ f o r w a r d _ p a s s ∗ ( 1 + f p _ t o _ b p _ r a t i o ) ∗ n _ p a s s e s training\_compute = ops\_per\_forward\_pass * (1 + fp\_to\_bp\_ratio) * n\_passes training_compute=ops_per_forward_pass∗(1+fp_to_bp_ratio)∗n_passes
通常估计fp_to_bp_ratio的值为2:1 。最终的公式为:
t r a i n i n g _ c o m p u t e = o p s _ p e r _ f o r w a r d _ p a s s ∗ 3 ∗ n _ e p o c h s ∗ n _ e x a m p l e s training\_compute = ops\_per\_forward\_pass * 3 * n\_epochs * n\_examples training_compute=ops_per_forward_pass∗3∗n_epochs∗n_examples
为什么反向传递操作与前向传递操作的比率2:1
计算反向传递需要为每一层计算与权重相关的梯度和每个神经元关于要回传的层输入的误差梯度。这些操作中的每一个需要的计算量大致等于该层前向传递中的操作量。因此,fp_to_bp_ratio约为2:1。
为什么权重更新参数计算可以忽略不计
在深度学习训练中,权重更新所需的参数计算量相对于前向传播和反向传播来说,通常可以被认为是可以忽略不计的。这主要有以下几个原因:
- 批量更新: 在深度学习中,通常使用批量梯度下降或小批量梯度下降等优化算法进行权重更新。这意味着权重更新是基于整个训练数据集或小批次的梯度。相比于前向传播和反向传播,其中需要对每个训练样本进行计算,权重更新的计算是在更大的数据集上进行的,因此其计算量相对较小。
- 累积梯度: 在实际应用中,通常会累积多个批次的梯度来更新参数。这样做有助于降低梯度的方差,提高梯度估计的稳定性。由于梯度的累积,单个批次中的权重更新计算相对于整体训练过程来说是较小的一部分。
- 参数共享: 在卷积神经网络(CNN)等架构中,存在参数共享的情况。在这种情况下,多个神经元共享同一组权重,从而减少了参数的数量。由于参数共享,权重的梯度计算是相对较小的。
前向传递计算和常见层的参数数量
下面是整理了一个常见神经网络层的表格,估算了它们的参数数量以及每层前向传递所需的浮点运算次数。
前文已经知道了,在许多层中,前向传递中的FLOP数量大致等于参数数量的两倍,然而,有许多例外情况,例如CNN由于参数共享而具有更少的参数,而词嵌入则不进行任何操作。
全连接层(Fully connected layer)

参数

浮点数计算量
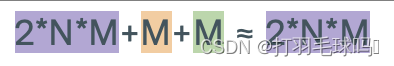
CNN
从形状为 H × W × C H \times W \times C H×W×C 的张量中使用形状为 K × K × C K \times K \times C K×K×C的 D 个滤波器,应用步幅为 S 和填充为 P 的卷积神经网络(CNN)。

参数
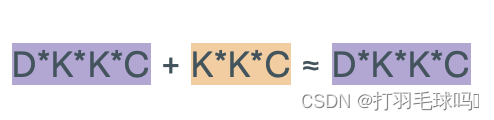
浮点数计算量
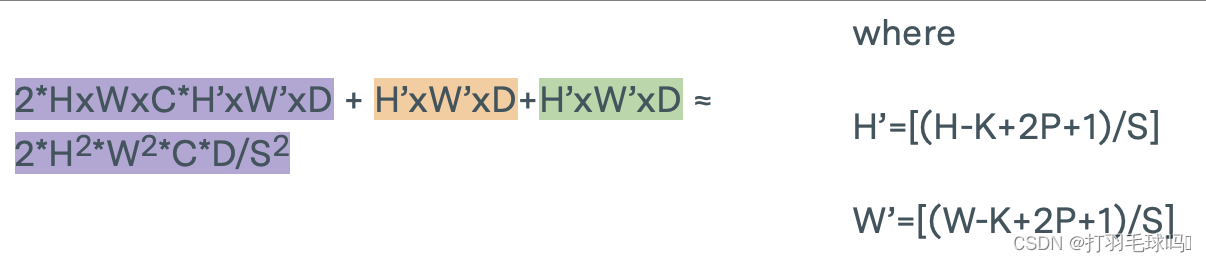
转置CNN
从形状为 H × W × C H \times W \times C H×W×C 的张量中使用形状为 K × K × C K \times K \times C K×K×C的 D 个滤波器,应用步幅为 S、填充为 P 的转置卷积神经网络(Transpose CNN)。

参数
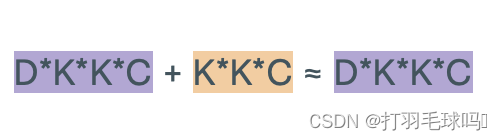
浮点数计算量
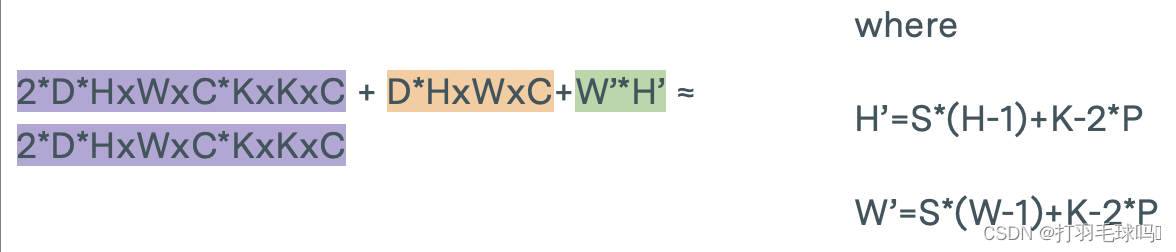
RNN
带有偏置向量的循环神经网络(RNN),其输入大小为 N,输出大小为 M。

参数

浮点数计算量
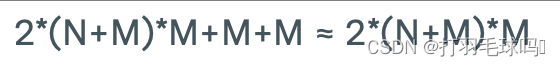
GRU
带有偏置向量的全门控门循环单元(Fully Gated GRU),其输入大小为 N,输出大小为 M。

参数
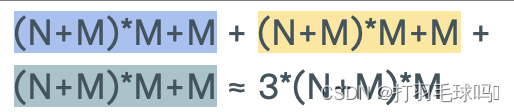
浮点数计算量
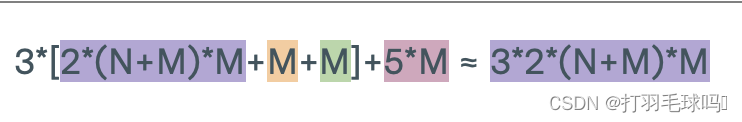
LSTM
带有偏置向量的长短时记忆网络(LSTM),其输入大小为 N,输出大小为 M。

参数
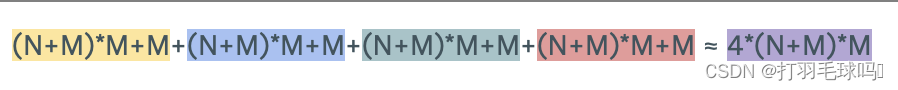
浮点数计算量
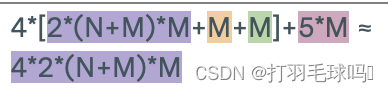
Self-Attention
具有序列长度 L、输入大小为 W、键大小为 D 和输出大小为 N 的自注意力层(Self-Attention Layer)。

参数
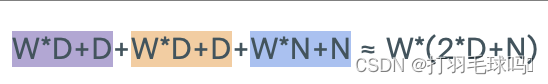
浮点数计算量

Multi-Headed Attention
具有序列长度 L、输入大小为 W、键大小为 D、每个注意力头输出大小为 N、最终输出大小为 M 以及 H 个注意力头的多头注意力层(Multi-Headed Attention Layer)。

参数
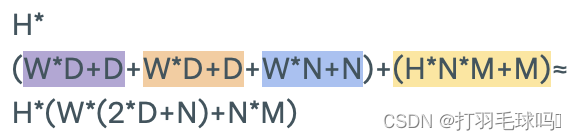
浮点数计算量
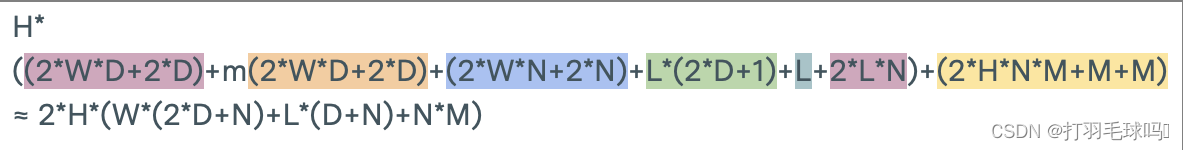
示例:CNN-LSTM-FCN模型
例如,假设我们有一个CNN-LSTM-FCN架构,具体如下:
- 输入是形状为 [400x400x5] 的图像序列。
- 每个输入序列的平均长度为20张图像。
- CNN 具有16个形状为 5x5x5 的滤波器,应用步幅为2,填充为2。
- LSTM 是一个多对一层,具有256个输出单元和偏置向量。
- 全连接层有10个输出单元。
- 训练过程经过10个时期,每个时期包含100个大小为128的序列批次。
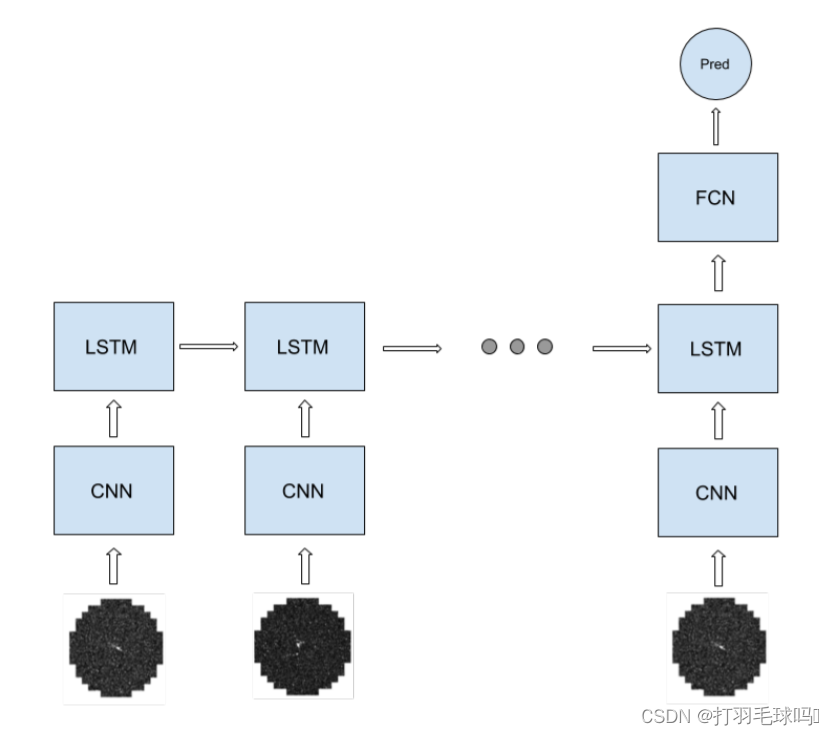
当我们考虑一个CNN-LSTM-FCN模型时,循环部分包括CNN和LSTM,而FC则是网络的非循环部分。
首先,CNN接受一个形状为 400 ∗ 400 ∗ 5 400 *400 * 5 400∗400∗5的输入图像序列。该CNN有16个5x5x5的滤波器,应用步幅为2,填充为2。它产生一个输出,宽度和高度为 H ’ = W ’ = [ ( W − K + 2 P ) / S ] + 1 = [ ( 400 − 5 + 2 ∗ 2 + 1 ) / 2 ] = 200 H’=W’= [(W -K +2P)/S]+1 = [(400 - 5+2 * 2+1)/2 ]=200 H’=W’=[(W−K+2P)/S]+1=[(400−5+2∗2+1)/2]=200,通道数为16。整个CNN的前向传递需要约 1.024 × 1 0 12 1.024 \times 10^{12} 1.024×1012 次浮点运算(FLOP)。
在将输入馈送到LSTM之前,CNN的输出被重新排列成一个 200 ∗ 200 ∗ 16 200*200*16 200∗200∗16的输入。然后,LSTM中每个序列标记的操作数量约为 1.31 × 1 0 9 1.31 \times 10^9 1.31×109FLOP。最后,全连接层(FC)有10个输出单元,它需要5120 FLOP。
整个网络的非循环部分相对较小,我们可以将总操作数近似为:
t r a i n i n g _ c o m p u t e ≈ o p s _ p e r _ f o r w a r d _ p a s s _ r e c u r r e n t × 3 × n _ e p o c h s × n _ b a t c h e s × b a t c h _ s i z e × a v g _ t o k e n s _ p e r _ s e q u e n c e ≈ 1.024 × 1 0 12 F L O P × 3 × 10 × 100 × 128 × 20 = 7.86432 × 1 0 18 F L O P training\_compute≈ops\_per\_forward\_pass\_recurrent \times 3 \times n\_epochs \times n\_batches \times batch\_size \times avg\_tokens\_per\_sequence ≈1.024 \times 10^{12}FLOP \times 3 \times 10 \times 100 \times 128 \times 20=7.86432×10 ^{18}FLOP training_compute≈ops_per_forward_pass_recurrent×3×n_epochs×n_batches×batch_size×avg_tokens_per_sequence≈1.024×1012FLOP×3×10×100×128×20=7.86432×1018FLOP
方法2:基于硬件设置和训练时间计算运算次数
另一种估算方法涉及考虑所使用的硬件和训练时间。我们将研究如何利用这些硬件方面的信息来估算计算资源的使用情况,并探讨硬件选择如何影响深度学习模型的性能和效率。
传统的基于硬件设置和训练时间计算运算次数是用使用GPU天数做为标准。
GPU使用天数:描述了单个GPU用于训练的累积天数。如果训练持续了5天,总共使用了4个GPU,那等于20个GPU天数。
传统的用GPU天数来估算计算资源的方法存在一些问题。首先,它只关注训练所使用的时间,而忽略了训练过程中所使用的计算硬件的性能。在十年内,GPU的性能显著提升,因此相同的GPU天数在不同时期所完成的实际计算工作量可能存在巨大差异。
此外,该方法没有考虑到不同硬件设置之间的差异。同样的GPU天数在不同的硬件配置下可能导致不同数量的浮点运算。因此,为了更准确地估算计算资源的使用情况,我们需要考虑硬件性能和配置的影响。
因此我们需要用GPU时间结合硬件配置估算FLOP,具体步骤如下
1.从论文/参考文献中提取信息:
在深入研究模型相关论文时,我们需要从中提取以下关键信息:
- GPU天数的数量:论文中应该包含关于训练模型所用GPU的天数,这反映了模型在训练期间的计算资源使用情况。
- 所使用的计算系统/GPU:论文应该明确说明在训练期间使用的计算系统或GPU型号,这对于了解硬件规格和性能至关重要。
- 训练运行期间使用的浮点数数字表示:论文应提供关于训练运行期间所采用的数字表示的信息,如FP32、FP16、BF16、INT8等。这直接关系到模型在计算过程中使用的精度。
2.阅读硬件规格
通过阅读硬件规格表,我们可以获取以下信息:
- GPU/系统的型号:通过查阅制造商的规格表,我们可以确定所使用的GPU或计算系统的具体型号。此信息对于计算性能的准确评估至关重要。
- GPU的峰值性能:规格表通常包含GPU的峰值性能,以FLOP/s(每秒浮点运算次数)为单位。这是评估硬件计算能力的关键指标。
以下是NVIDIA A100的示例:
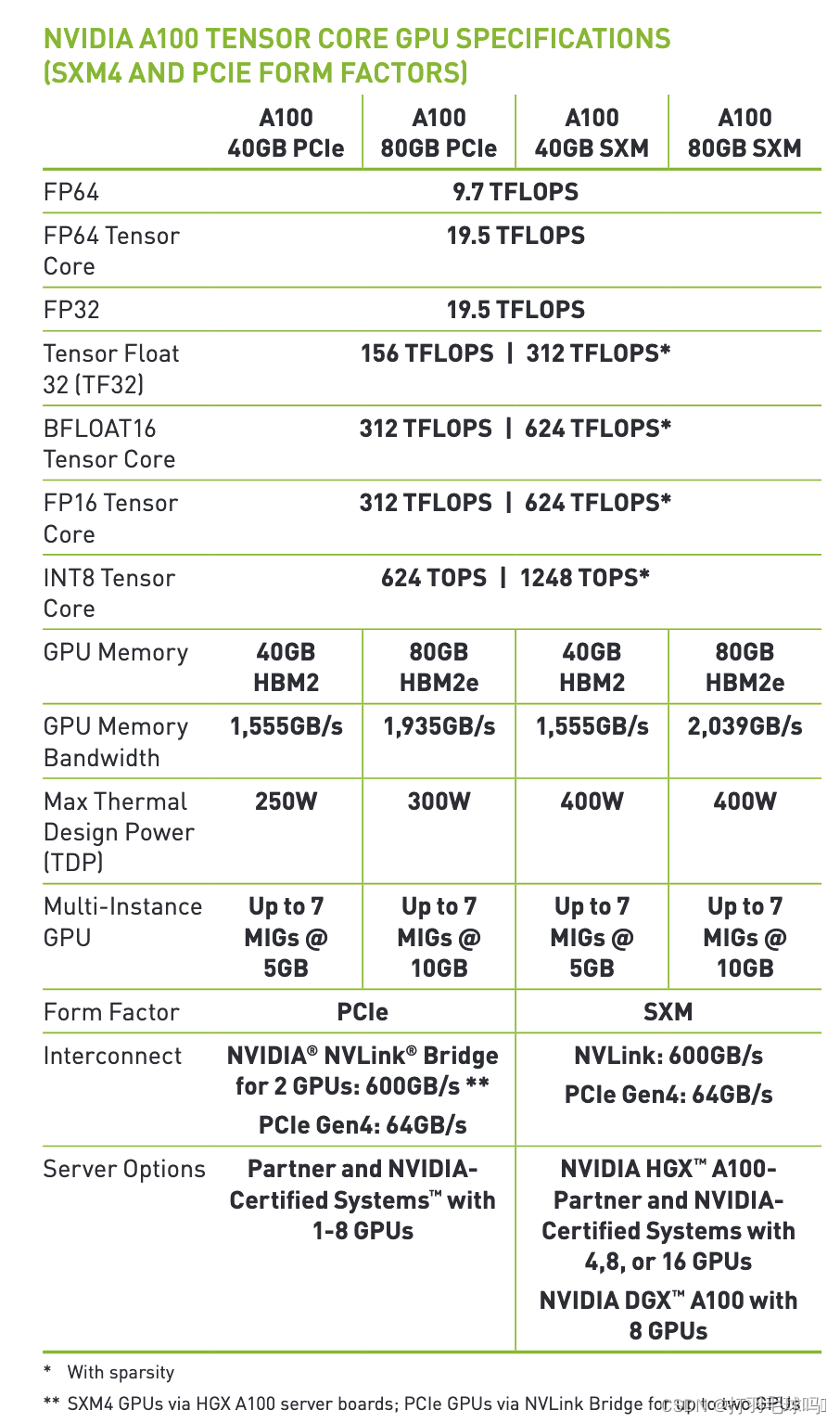
如果您找不到使用过的硬件或上述硬件的规格,建议参考下面链接里的表格,估计给定年份的平均计算能力。您还可以在下面的框中找到每年峰值表现的图表。
ML Hardware Data sheet
3.进行估算
综合上述信息,我们可以进行如下估算:
估算GPU的总FLOP:
步骤 1:计算单个GPU的峰值性能
从硬件规格表中获取GPU的峰值性能,表示为FLOP/s。例如,若峰值性能为 X X X FLOP/s。
步骤 2:计算总的GPU FLOP
通过将单个GPU的峰值性能乘以GPU使用的天数,我们得到总的GPU FLOP。假设GPU使用天数为 Y 天,那么总的GPU FLOP 为 X × Y X \times Y X×Y。
精度的考虑:
步骤 1:确定训练使用的数字表示
从论文中获取模型在训练期间使用的数字表示,如FP32、FP16等。
步骤 2:确定每个数字表示的FLOP数
根据不同数字表示的标准,确定每个数字表示所需的FLOP数。例如,FP32可能需要 A A A FLOP,FP16可能需要 B B BFLOP。
步骤 3:计算总的FLOP数
将每个数字表示所需的FLOP数与模型中相应数字表示的使用情况相乘,得到总的FLOP数。假设使用了FP32和FP16,总FLOP数为
A × 数量 1 + B × 数量 2 A×数量1+B×数量2 A×数量1+B×数量2。
考虑硬件特性:
步骤 1:检查是否使用了张量核心
查阅硬件规格表或相关文献,确定是否启用了NVIDIA的张量核心。如果启用,我们可以考虑这一特性对性能的影响。
步骤 2:了解张量核心的使用情况
若启用了张量核心,了解它在模型训练中的具体使用情况。这可能涉及到特殊的参数设置或架构要求。
步骤 3:调整总的GPU FLOP
如果使用了张量核心,可以根据其使用情况调整总的GPU FLOP。这可能需要根据具体情况进行一些额外的计算和估算。
通过这些详细的步骤,我们可以更准确地估算模型在训练期间的计算资源使用情况,考虑到不同精度和硬件特性的影响。
)






-java)




)






