文档讲解:代码随想录
视频讲解:代码随想录B站账号
状态:看了视频题解和文章解析后做出来了
1143.最长公共子序列
class Solution:def longestCommonSubsequence(self, text1: str, text2: str) -> int:dp = [[0] * (len(text2) + 1) for _ in range(len(text1) + 1)]for i in range(1, len(text1) + 1):for j in range(1, len(text2) + 1):if text1[i-1] == text2[j-1]:dp[i][j] = dp[i-1][j-1] + 1else:dp[i][j] = max(dp[i-1][j], dp[i][j-1])return dp[len(text1)][len(text2)]- 时间复杂度:O(n^2)
- 空间复杂度:O(n)
1. 确定dp数组的含义
dp[i] 为下标范围为0到i+1之间,最长的自增序列的长度。
2. 确定递推公式
因为本题规定了自增序列可以不连续,所以我们不能只和前一个元素对比,而是和所有前面的元素对比,如果大于前面的某个元素,就在那个元素的基础上+1,当然我们要一直保留最大值。
所以dp[i] = max(dp[j] + 1, dp[i])
其中i是当前元素,j是i之前的某个元素。
3. dp数组初始化
因为我们要返回的是长度,而每个元素单独长度已经为1了,所以所有元素都先初始化为1。
4. 确定遍历顺序
递推公式中的j是i之前的元素下标,所以从前往后递推。
5. 举例
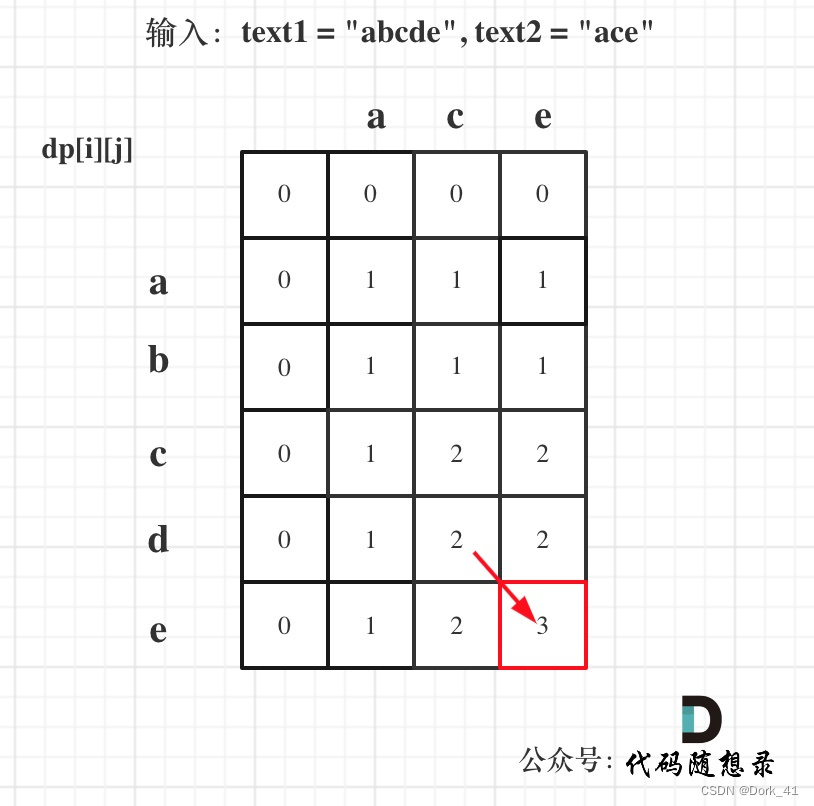
1035.不相交的线
class Solution:def maxUncrossedLines(self, nums1: List[int], nums2: List[int]) -> int:dp = [[0] * (len(nums2) + 1) for _ in range(len(nums1) + 1)]for i in range(1, len(nums1) + 1):for j in range(1, len(nums2) + 1):if nums1[i-1] == nums2[j-1]:dp[i][j] = dp[i-1][j-1] + 1else:dp[i][j] = max(dp[i-1][j], dp[i][j-1])return dp[len(nums1)][len(nums2)]- 时间复杂度:O(n^2)
- 空间复杂度:O(n)
和前一题完全一样,改个变量名直接ac了。
53. 最大子序和
class Solution(object):def maxSubArray(self, nums):dp = [0] * len(nums)dp[0] = nums[0]for i in range(1, len(nums)):dp[i] = max(dp[i-1] + nums[i], nums[i])return max(dp)- 时间复杂度:O(n^2)
- 空间复杂度:O(n)
1. 确定dp数组的含义
dp[i] 为下标范围为 0 到 i 之间的最大子序和。
2. 确定递推公式
两种情况:
第一种:取当前元素和上一个元素的最大子序和
第二种:不考虑之前元素,把当前元素当作起始点
通过比较这两个值定义dp[i]的值。第二种的逻辑在于,如果当前元素的值都已经大于之前最大子序和 + 当前元素,那么之前子序和一定是负的,对于找到最大子序一定没有帮助,那么还不如从当前元素开始另起一个子序。
3. dp数组初始化
dp[0]初始化为第一个元素的值,从第二个元素开始遍历。
4. 确定遍历顺序
递推公式需要之前的元素下标,所以从前往后递推。
5. 举例
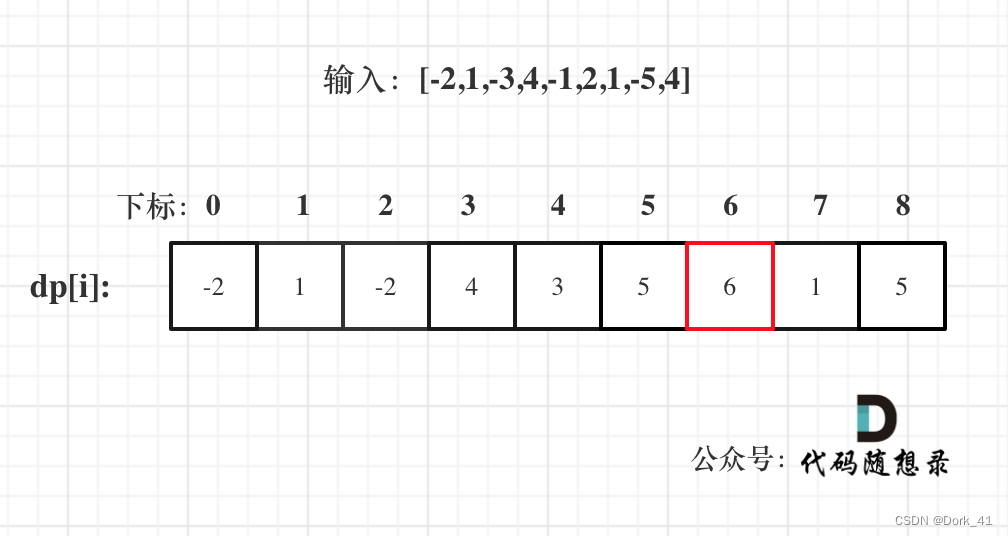









)




(C:前缀和+滑动窗口,E:位运算加分块))




C语言之符号常量概述)