目录
1 概述
2 数学模型
2.1 问题表述
2.2 DG的最佳位置和容量(解析法)
2.3 使用 GA 进行最佳功率因数确定和 DG 分配
3 仿真结果与讨论
3.1 33 节点测试配电系统的仿真
3.2 69 节点测试配电系统仿真
4 结论
1 概述
为了使系统网损达到最低值,人们提出了多种方法来确定分布式发电机组的最优位置和容量。
本文将解析法和遗传算法相结合,用于配电网中多个分布式电源的优化配置,使系统网损最小。
这种组合保证了多个分布式发电机组配置的收敛精度和速度。在本文中,在配电网网损最小化时,同时考虑分布式电源的有功功率、功率因数和位置。如果DG是由DG所有者安装的,则该实用程序将仅规定DG的最大发电量。但是,如果DG是由它安装的,则DG的大小和位置都将由该实用程序确定。将该方法应用于33节点和69节点试验配电网。仿真结果表明,与其他方法相比,该方法具有更低的损耗。
本文提出了一种新的方法,这是一种混合方法,它使用遗传算法搜索大范围的位置组合和分布式电源的功率因数,并采用解析方法计算每个分布式电源的位置和容量。虽然这是以要求预先指定DG单位的数量为代价来实现的,但这为检验不同数量 DG 战略布局的好处开辟了潜力。
将该方法应用于33节点和69节点试验配电网,结果表明了该方法在配电网分布式发电机组优化配置中的准确性和有效性。本文创新点如下:
分析和启发式搜索方法相结合,同时实现高速和准确的收敛。考虑将松弛节点的有功潮流对分布式电源产生的有功功率的依赖性作为最小化配电网网损的新约束。
利用分布式电源最优输出有功功率的确定性方程,根据网损系数和网络需求,对配电网网损最小化问题进行了解析解。在最小化配电网损耗的过程中,同时考虑分布式电源的有功功率、功率因数和位置。
本论文的结构如下:第二节数学模型
第三节对多个DG单元放置的仿真和结果进行了研究和讨论。最后,第四节对本文进行了总结。
2 数学模型
2.1 问题表述
网络中的有功网损可以表示为不同机组发电量的函数,根据下面的关系,称为Kron方程:

等式(1)可以表示为以下矩阵形式:
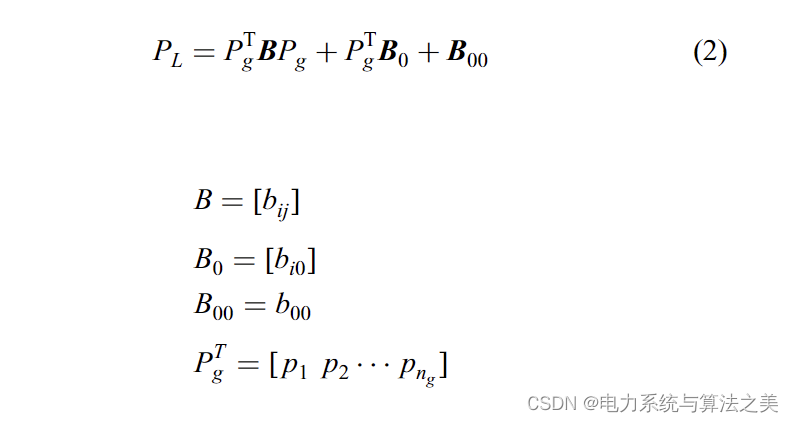
在(2)中,矩阵B、B0和B00是损耗系数矩阵。一般来说,这些系数不是恒定的,并且依赖于负荷值和发电量。但是,它们可以在系统运行的基本情况下计算。
本文考虑了如下假设:配电网是一个在松弛节点馈电的放射状系统,用数字1标识并连接到子配电电网络或输电网络,分布式电源具有恒定的功率因数。
2.2 DG的最佳位置和容量(解析法)
假设在使用恒定功率因数,
,.....
的母线Kn1、Kn2、...中安装了Ng个DG单元。假设松弛母线为发电单元,则该网络中有
个发电单元。网损可按(1)计算。
假设DG安装在母线2、3、…、+1上。如果(1)相对于
的导数为零,则网络损耗将是最小的。
应当注意,...
在(1)中指示由不同DG产生的功率是独立的,并且由松弛母线
产生的功率如下所示依赖于这些变量:
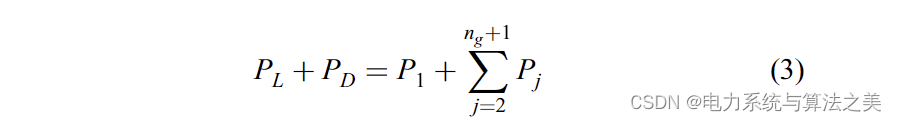
应当注意,假设PD在网络的特定状态下是恒定的。
对(3)进行微分,可以得到 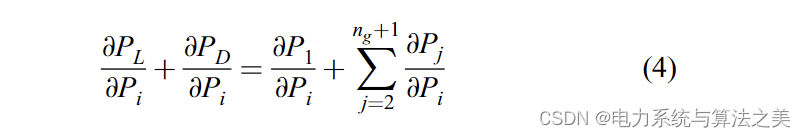
由于 ∂PL/∂Pi 和 ∂PD/∂Pi 等于 0,所以 (4) 可以写成如下:
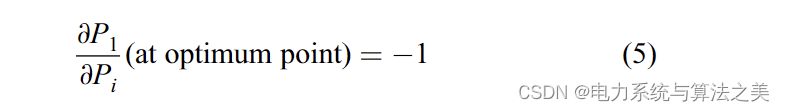
如(5)所示,P1取决于不同DG的发电量。另一方面,在系统损耗最小的情况下,松弛母线产生的有功功率变化与DG机组产生的有功功率变化的比值等于-1。为了使(1)在(3)的约束下达到最小,采用了拉格朗日松弛法,具体如下:
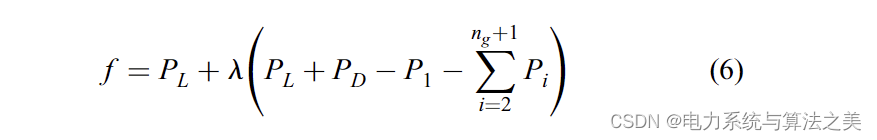
偏微分函数应该等于零,也就是:
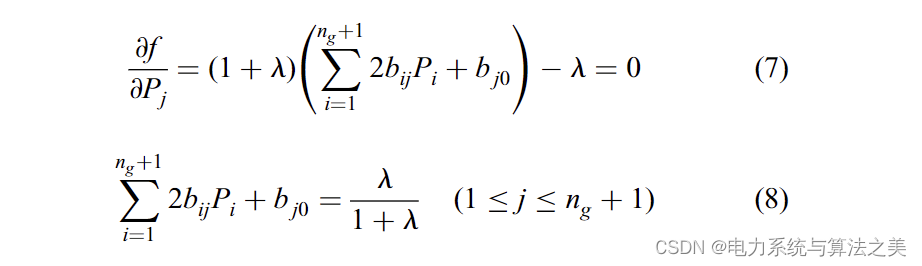
方程(8)可以写成矩阵形式,如下:
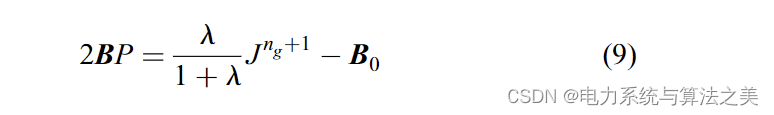
+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
可以使用以下等式从 (9) 计算 P:

其中 x、E 和 F 可以分别根据以下等式计算:
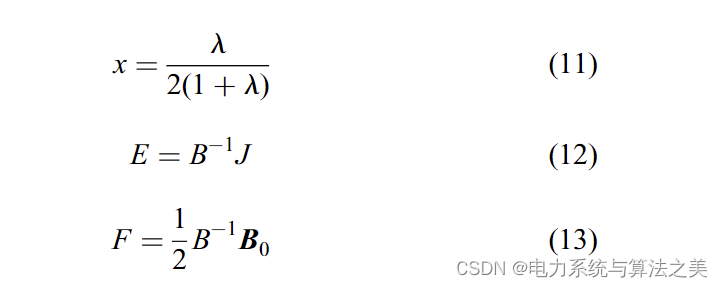
P的每个元素确定如下:
![]()
对于已知的x值,可以根据(10)计算出最佳的,将(10)-(14)代入(3),可以写出以下公式:
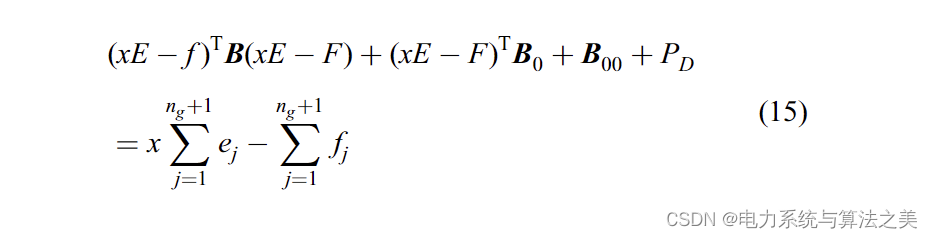
+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
展开 (15) 得出以下等式:
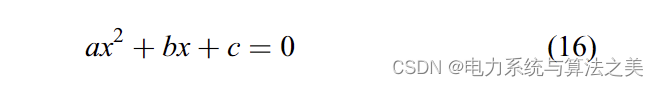
其中参数 a、b 和 c 基于以下等式计算:
a通过下式进行计算:

通过将 E 从 (12) 中代入, (17) 可以写为:
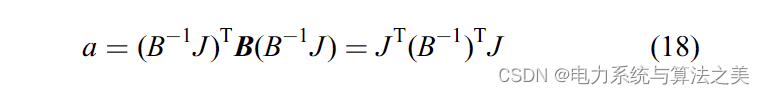
由于 B = BT, (18) 可简化如下:
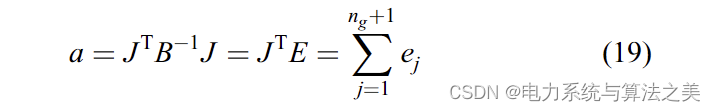
b 根据以下等式计算:
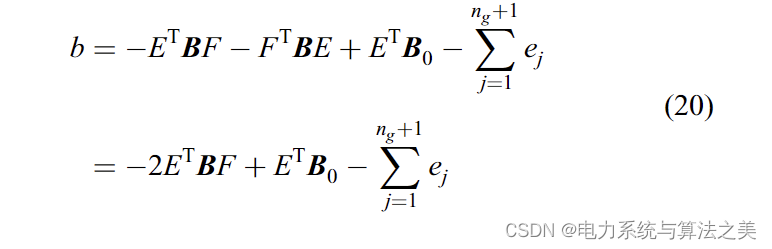
考虑 (13),b 可以根据以下等式计算:
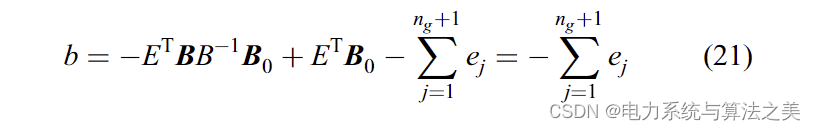
最后,c可以按下式进行计算:
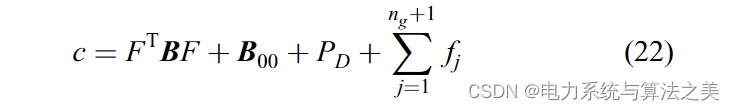
等式 (16) 有如下两个根:
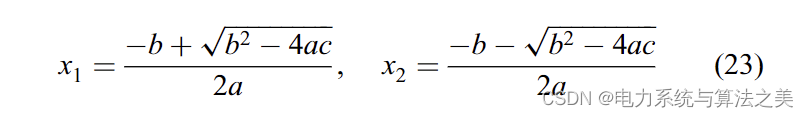
由于 b 是负数 [考虑 (21)],x1 是一个很大的数,对应的 Pi 也有很大的值 [根据 (14)]。这个答案是不可接受的,因为单位中的 Pi 太大了。因此,以下答案是唯一可以接受的答案:
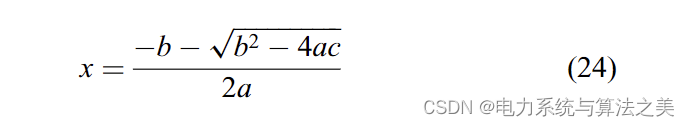
使用 (10)–(24),确定 的最佳值。
2.3 使用 GA 进行最佳功率因数确定和 DG 分配
在本节中,DG功率因数及其位置被确定为具有系统损耗的最小值。遗传算法是一种通用的优化方法,已被用于不同领域的优化问题。遗传算法分几个步骤进行,如:
在本文中,每个DG单元的优化问题都考虑了三个变量。这些变量是DG的有功功率、DG的功率因素和DG的位置。DG的有功功率是通过解析方案和数学方法得到的(24)。功率因数和DG的位置分别通过使用连续和离散的GA来确定。在GA中,染色体是问题变量,也就是功率因数和DG的位置。因此,假设有ng个DG单元,GA中染色体的长度将等于2ng,包括ng个功率因数的基因(PF1, PF2, ..., PFn)和ng个DG连接位置的基因(D1, D2, ..., Dn)。

图1 本文所考虑的染色体形态。
换句话说,在GA过程的第一步,一组可能的答案被随机产生,这些答案被称为方案或染色体。本文认为一个染色体的形式如图1所示。在下一步中,将根据每个染色体的适合度为其分配一个数字,作为可能的答案。上述数字由适应度函数决定,适应度函数将由GA进行优化。最后,GA通过选择操作符并根据染色体的适配度选择一些染色体进行交叉、变异和替换操作。这些运算符产生一个新的群体,该过程将被重复,直到达到停止条件。为了计算与染色体相对应的适配函数,根据(2)计算网络损失,并利用(24)确定DG的最佳功率世代。在功率流运行后,根据(1)确定电力系统损失,并将其分配给一个染色体作为其适配值。
![]()
GA 应该通过改变功率因数和不同 DG 的位置来寻找适应度函数的最小值。本文采用分析方法和启发式搜索方法相结合的方法解决了分布式电源优化分配问题,如图 2 所示。使用该方法的主要好处如下:
由于分布式电源的功率余量代数太广,GA收敛速度慢,可能无法得出准确的解。本文采用遗传算法确定分布式发电机组的安装位置及其功率因数,并采用解析法确定分布式发电机组产生的最佳功率。
仅使用解析方法会导致复杂且非线性的方程,因为应计算损耗系数相对于 DGs 功率因数的微分,并且损耗系数是 DGs 功率因数的非线性和复杂函数。此外,DGs 位置是一个离散参数,它对 DG 位置的导数是没有意义的。因此,启发式搜索算法应该被用于优化DG分配。考虑到这两个问题,本文提出了分析和启发式搜索相结合的方法。
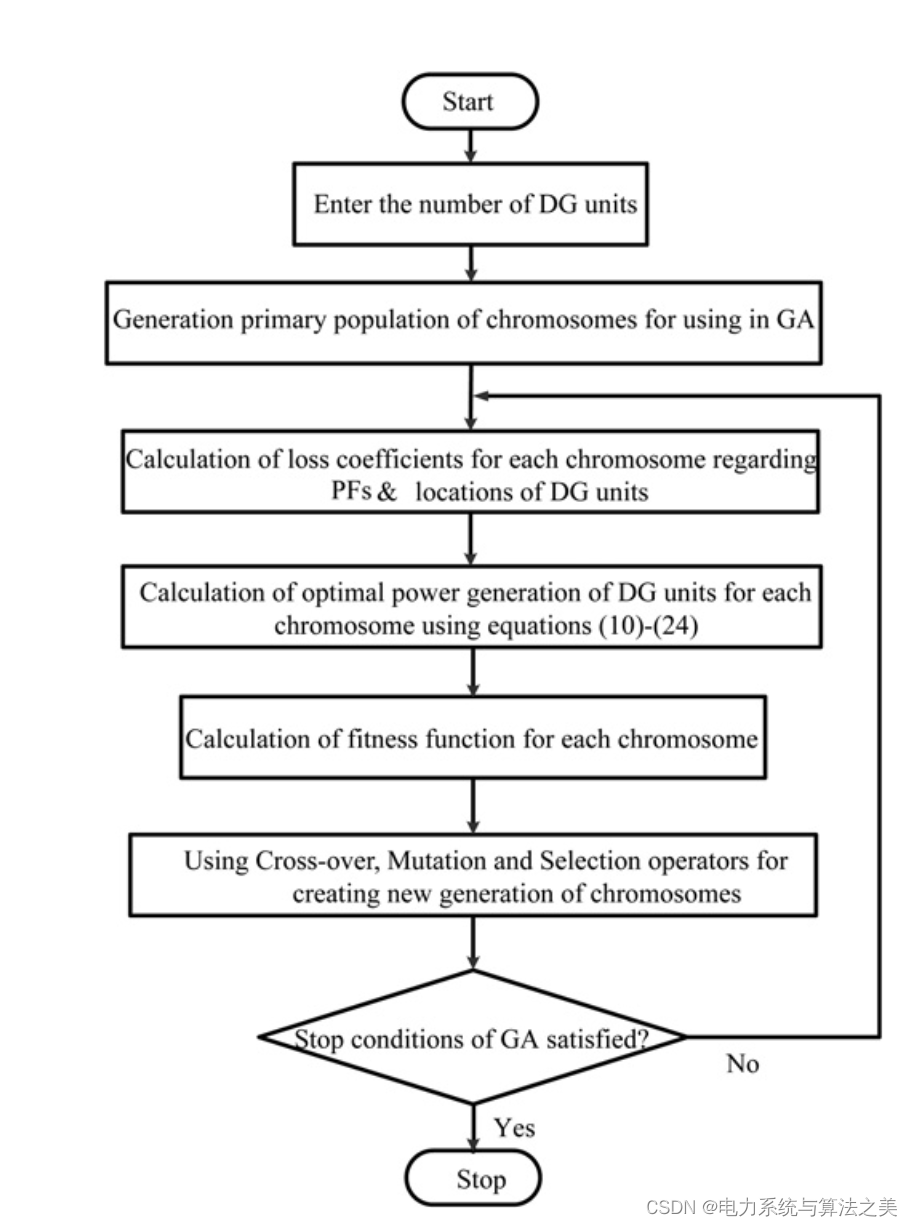
图2 所提出方法的流程图
3 仿真结果与讨论
将该方法应用于图3和图4所示的两个试验配电网(33节点和69节点系统)。该算法在Matlab环境下实现,并使用MATPOWER软件进行潮流计算。
在本研究中,分布式发电有两种不同的运行模式:分布式发电只产生有功功率(单位功率因数模式)和分布式发电可以产生有功和无功(非单位功率因数模式)。
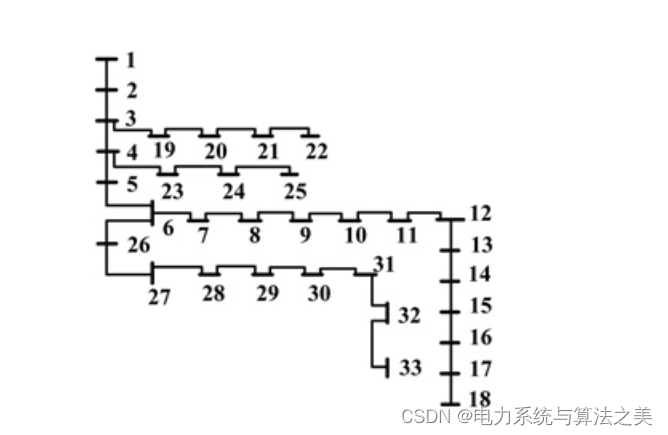
图3 33节点测试配电系统
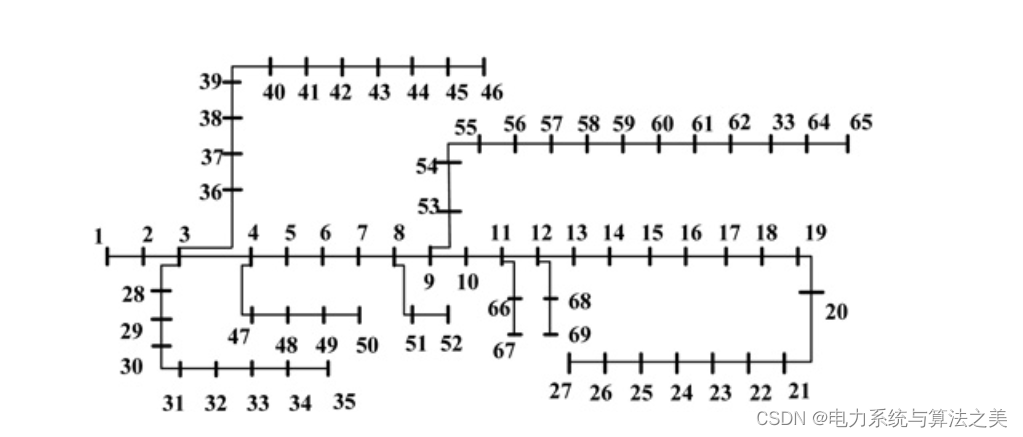
图4 69节点测试配电系统
3.1 33 节点测试配电系统的仿真
本节将在以下两种情况下考虑两种不同的DG运行模式。
3.1.1 情景1:DG运行的统一功率因数模式。
在这种情况下,假设DG产生有功功率,而不产生/消耗无功功率。使用建议的方法在网络中分配不同数量的DG。在表1中,建议的方法与其他方法进行了比较,即损失敏感系数(LSF)、改进的分析法(IA)和穷举负载流(ELF)方法[33]。从表1中可以看出,所提出的方法在降低损耗方面比其他方法有更好的表现。在放置一个DG的情况下,在这四种算法中,有三种算法建议在母线6上安装DG。为了显示建议的方法在寻找安装在母线6的DG的最佳发电量方面的性能,计算了网络损耗与安装在母线6的DG的发电量,如图5所示。如图5所示,如果安装在母线6上的DG产生2.706兆伏安,则损失达到最小值(0.09922兆瓦)。如表 1 所示,建议的方法找到了这个功率值,即安装在母线 6 上的 DG 应该产生的功率,以使损耗最小。
表 1 第一种场景的仿真结果(33节点测试配电系统)
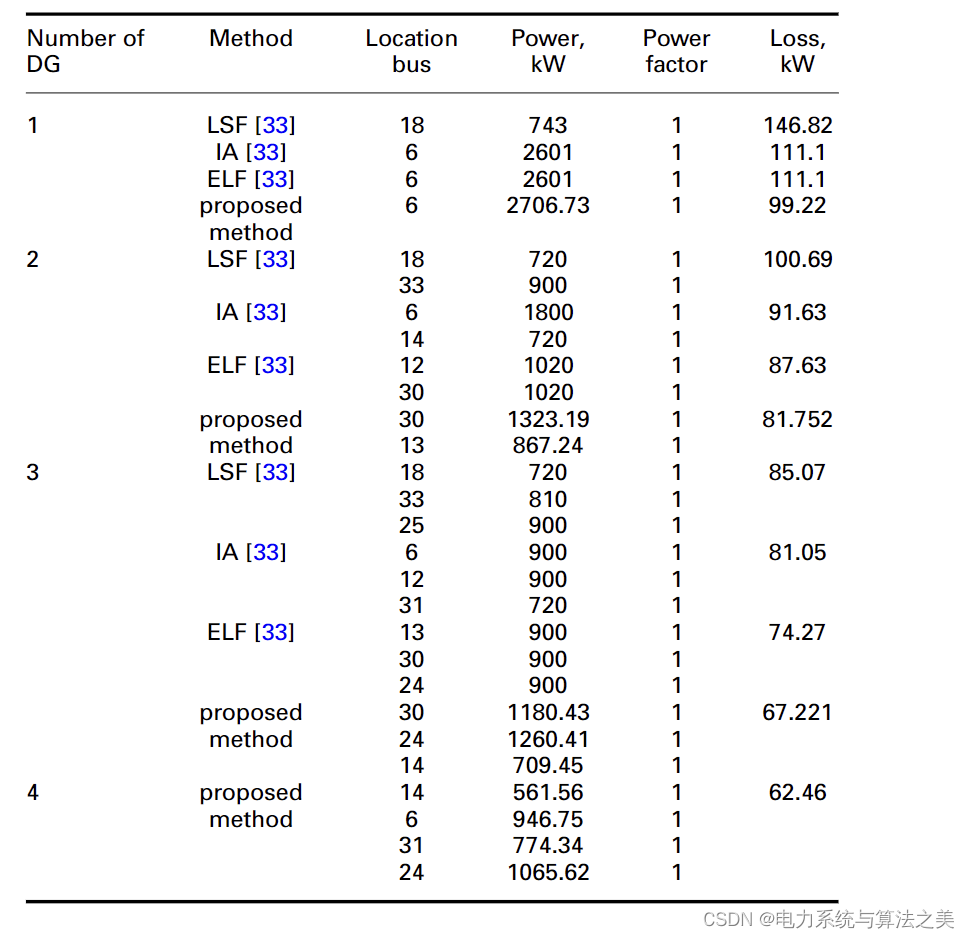
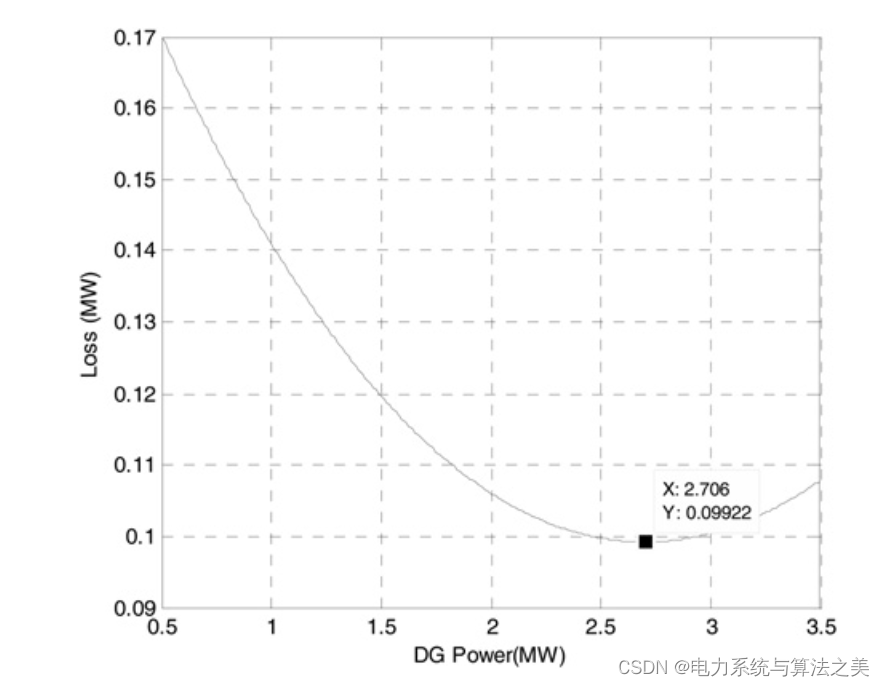
图5 发电量的网络损耗(DG安装在 6节点)
3.1.2 情景二:非统一功率因数的DG运行模式。
在这种情况下,假设DG的功率因数不一定等于1,仿真结果见表2。从表2中可以看出,建议的方法达到了最低的网络损耗。
在放置一个 DG 的情况下,建议的算法建议安装在母线 30。安装的 DG 的功率为 1844.85 kVA,滞后功率因数为 0.767。图 6 显示了损耗与 DG 位置及其功率因数的关系。如图所示,解析法和遗传算法相结合,通过在母线 30 上安装一台 DG(图 7)以 0.767 的滞后功率因数,达到了最小的网络损耗。为了解析解决该问题,总线的电压不等式约束(即 Vmin < V bus < V max)不能包含在优化问题中。因此,在优化程序完成后,可以而且应该检查母线电压和线电流,以保证母线电压的不等式约束。表3列出了安装DG机组后33个总线系统的最低和最高电压.
表 2 场景二(33节点测试配电系统)的仿真结果

表3 安装DG后的33个节点测试配电系统的最低和最高电压
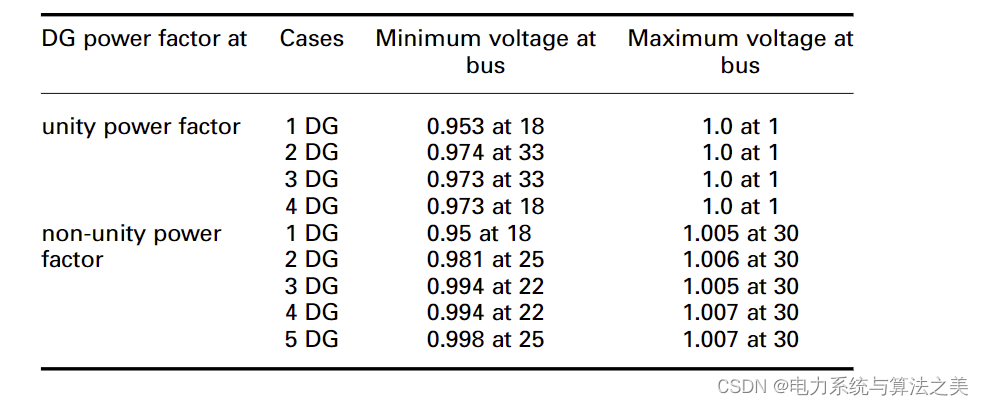
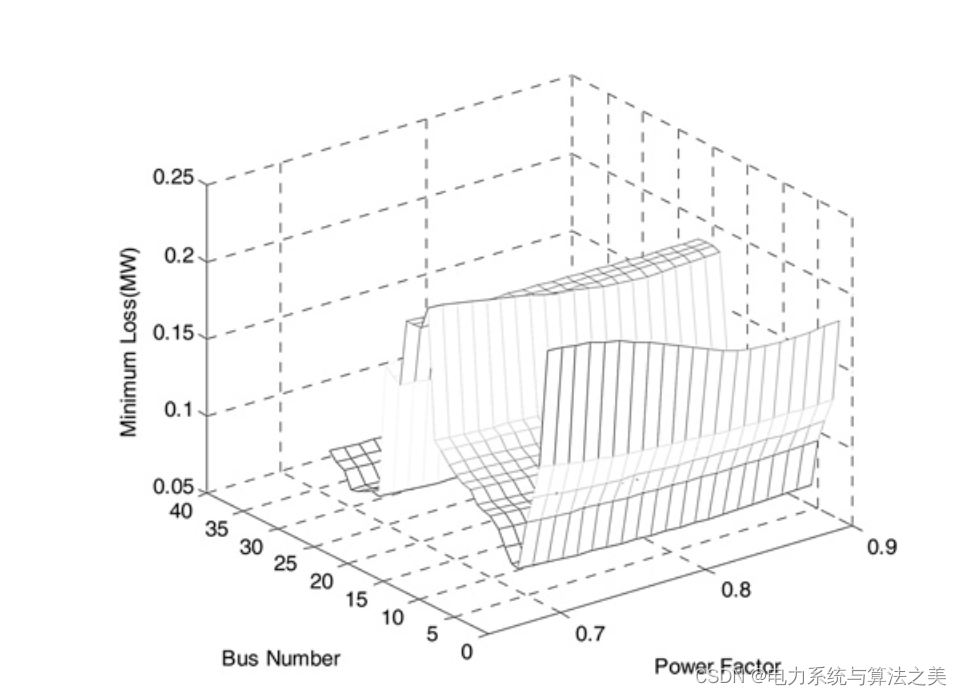
图 6 系统损耗与 DG 位置及其功率因数的关系

图7 在母线30安装一个DG,网络损失的最小值
3.2 69 节点测试配电系统仿真
本节对69 母线测试配电系统进行仿真。以下两种场景分别考虑了两种不同的 DG 运行模式。
3.2.1 场景一:DG 运行的单位功率因数模式:
这种情况下,假设 DG 工作在单位功率因数模式,只能产生有功功率。 DG 分配的结果列于表 4。如表中所列,与其他方法相比,所提出的方法导致较低的网络损耗。
表 4 第一种场景(69节点测试配电系统)的仿真结果
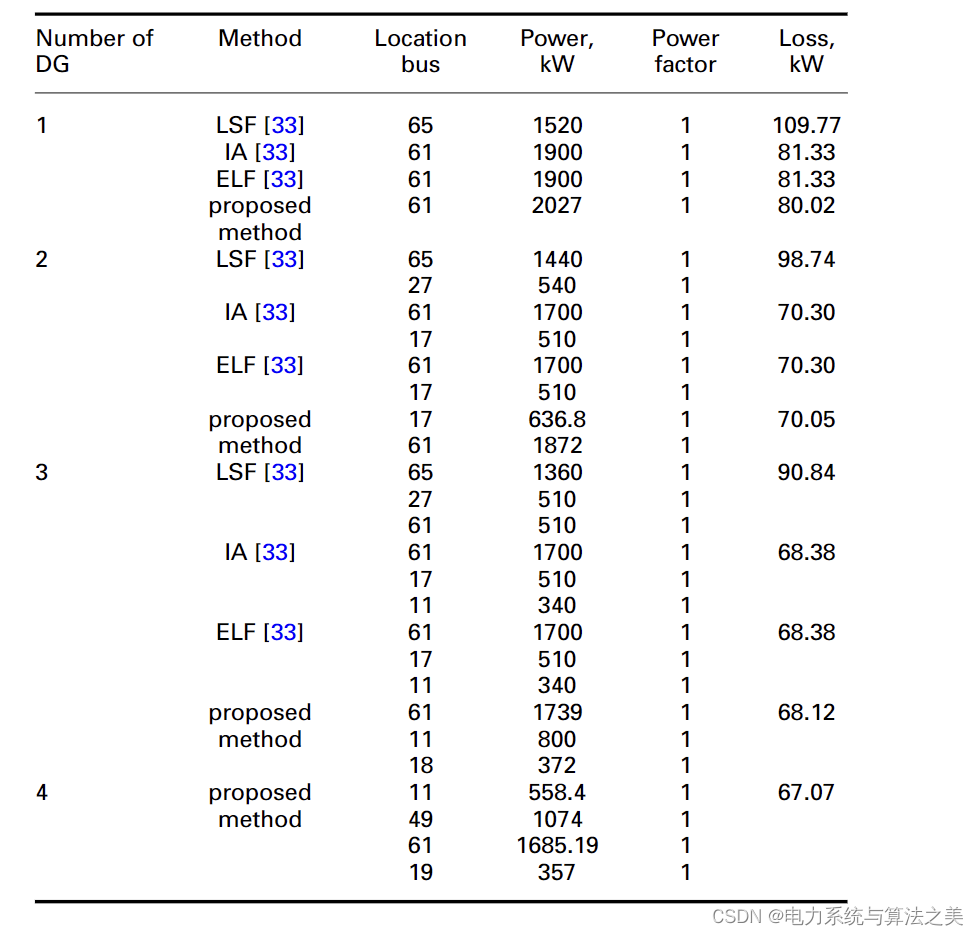
3.2.2 场景二:DG 运行的非统一功率因数模式:
此时 DG 可以产生有功和无功功率,其功率因数不一定等于 1。69 年 DG 优化配置的结果母线测试配电系统见表 5。表 6 列出了 DG 机组安装后 69 母线系统的最小和最大电压。
表 5 场景二(69节点测试配电系统)的仿真结果
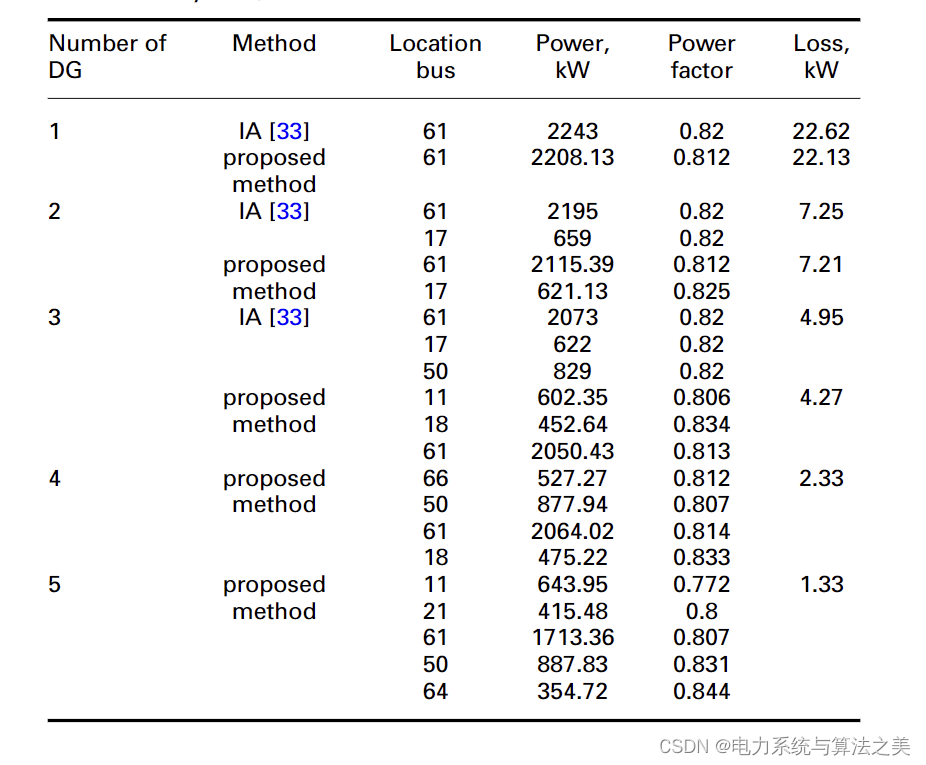
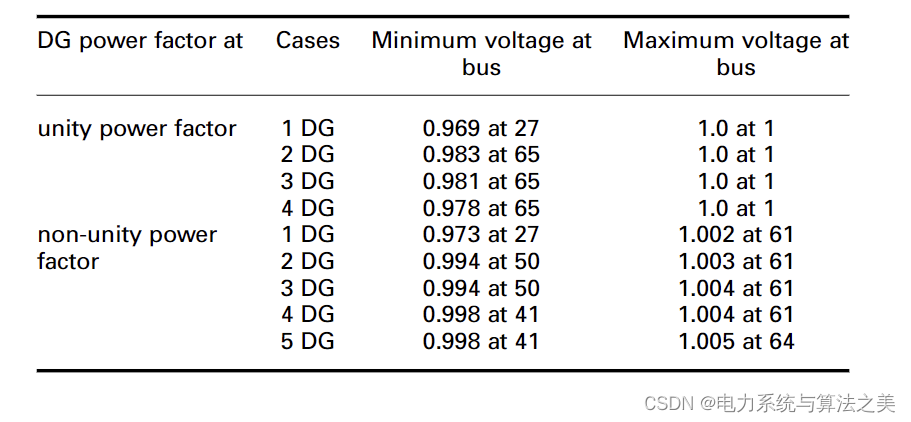
表 6 DG 安装后 69 母线测试配电系统的最小和最大电压
4 结论
本文提出了一种解析法和遗传算法相结合的方法,用于配电网多台分散发电机组的配置,使系统网损最小。该方法利用遗传算法来寻找分布式电源的最优安装位置,并使用一种新的解析公式来确定分布式电源容量。将该方法与IA、LSF和ELF方法在降低损耗方面进行了比较。结果表明,与其他方法相比,该方法达到了最低的损耗。







)
)


)
方法函数)






