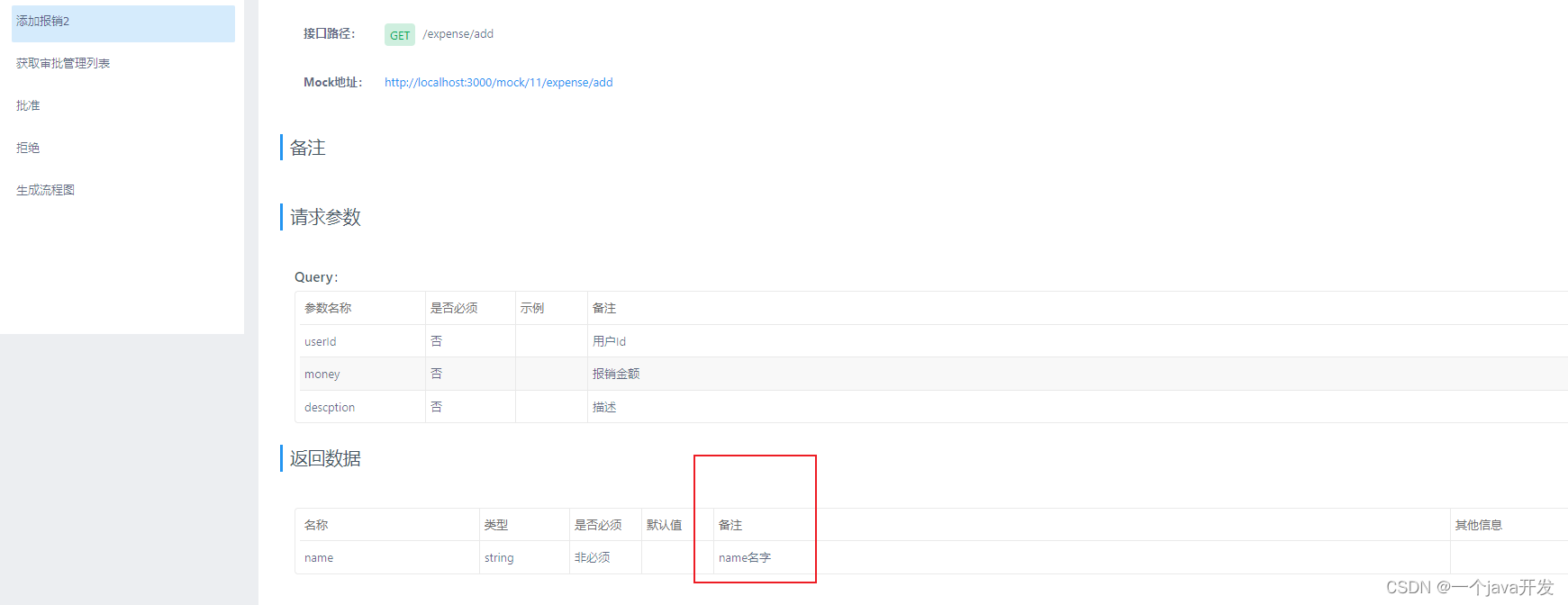
比如模块A中有个MyDemoEntity类，在B中以依赖的形式引入了A，并在B的接口中以MyDemoEntity作为返回值，导出到YAPI发现MyDemoEntity的备注没了。

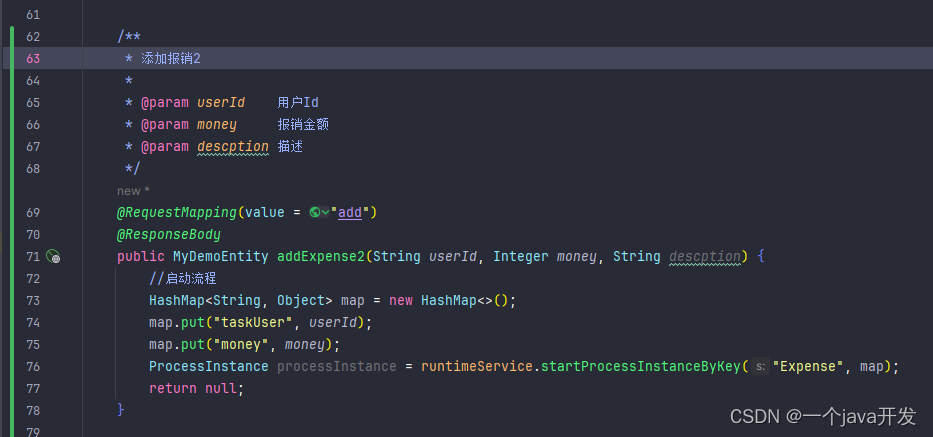
解决：

将A的内容安装到本地MAVEN仓库，并且需要将源码也一起安装

 <build><resources><resource><directory>target/classes</directory></resource></resources><plugins><plugin><groupId>org.apache.maven.plugins</groupId><artifactId>maven-source-plugin</artifactId><version>3.2.1</version> <!-- 使用最新的插件版本 --><executions><execution><id>attach-sources</id><phase>verify</phase> <!-- 通常在 verify 阶段执行 --><goals><goal>jar</goal></goals></execution></executions></plugin></plugins></build>

刷新B，导出到YAPI，解决