C语言实现堆栈和队列(动态)

行路难！行路难！多歧路，今安在？长风破浪会有时，直挂云帆济沧海。————李白

一  .堆栈

1 什么是堆栈

堆栈是一种特殊的线性表，堆栈中的元素以及元素之间的逻辑关系和线性表完全相同。在操作上的差别是线性表允许在任意位置插入和删除元素，而堆栈只允许在固定一端插入和删除元素，堆栈中允许插入和删除元素的一端称为栈顶，另一端称为栈底。

栈顶的当前位置是动态的，用于标记栈顶当前位置的变量，称为栈顶指示器。堆栈的插入操作，通常称为入栈。堆栈的删除操作通常称为出栈。

根据堆栈的定义，我们可以发现，每次入栈的元素都放在原栈顶元素之前而成为新的栈顶元素，每次出栈的元素都是原栈顶元素。这样最后进入栈的元素总是最先退出栈的，因此堆栈也称作后进先出的线性表，或简称为后进先出表。 

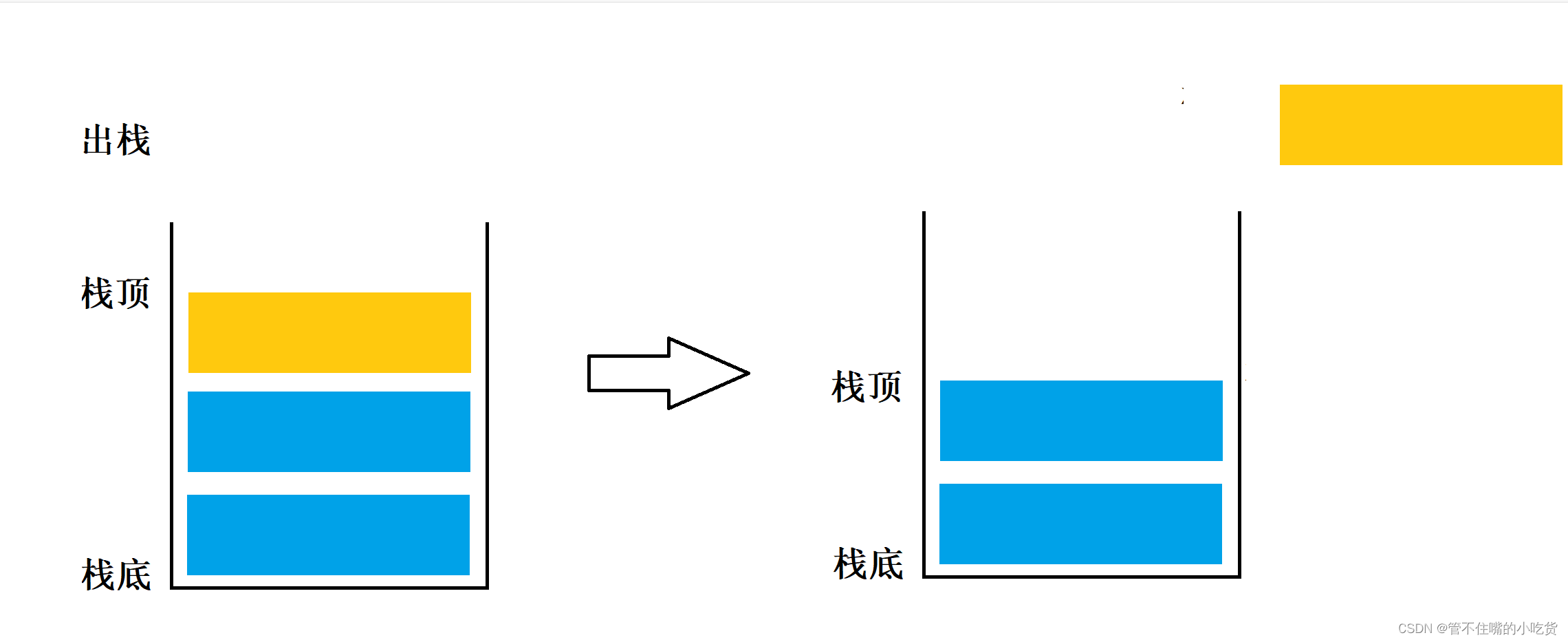
2 堆栈的两种实现方式

栈的实现一般可以使用数组或者链表实现

链式栈：用链表的结构来实现栈。

顺序栈：用数组的结构来实现栈。

优缺点：

单向链式结构的出栈入栈效率比较低，因为我们要先找到尾结点再行插入删除

而顺序栈只需要记录栈顶位置，进行出栈入栈十分方便，不需要多余的空间存储地址。

所以相对而言数组的结构实现更优一些。因为数组在尾上插入数据的代价比较小。

3 堆栈的操作实现

3.1 栈的结构体和初始化

结构体：

#pragma once#include <stdio.h>
#include <stdbool.h>
#include <assert.h>
#include <stdlib.h>
typedef int STDataType;typedef struct Stack
{STDataType* a;int top;int capacity;
}ST;

初始化：

void StackInit(ST* ps)
{assert(ps);ps->a = (STDataType*)malloc(sizeof(STDataType) * 4);if (ps->a == NULL){printf("malloc fail\n");exit(-1);}ps->capacity = 4;ps->top = 0;
}
3.2 销毁
void StackDestory(ST* ps)
{assert(ps);free(ps->a);ps->a = NULL;ps->top = ps->capacity = 0;
}

3.3入栈
// 入栈
void StackPush(ST* ps, STDataType x)
{assert(ps);// 满了-》增容if (ps->top == ps->capacity){STDataType* tmp = (STDataType*)realloc(ps->a, ps->capacity * 2 * sizeof(STDataType));if (tmp == NULL){printf("realloc fail\n");exit(-1);}else{ps->a = tmp;ps->capacity *= 2;}}ps->a[ps->top] = x;ps->top++;
}
3.4出栈
// 出栈
void StackPop(ST* ps)
{assert(ps);// 栈空了，调用Pop，直接中止程序报错assert(ps->top > 0);//ps->a[ps->top - 1] = 0;ps->top--;
}
3.5判断栈是否为空
bool StackEmpty(ST* ps)
{assert(ps);return ps->top == 0;
}
3.6取顶部数据
STDataType StackTop(ST* ps)
{assert(ps);// 栈空了，调用Top，直接中止程序报错assert(ps->top > 0);return ps->a[ps->top - 1];
}
3.7取栈中有效数据的个数
int StackSize(ST* ps)
{assert(ps);return ps->top;
}

4 完整代码

Stack.h
#pragma once#include <stdio.h>
#include <stdbool.h>
#include <assert.h>
#include <stdlib.h>
typedef int STDataType;typedef struct Stack
{STDataType* a;int top;int capacity;
}ST;void StackInit(ST* ps);void StackDestory(ST* ps);
// 入栈
void StackPush(ST* ps, STDataType x);
// 出栈
void StackPop(ST* ps);STDataType StackTop(ST* ps);int StackSize(ST* ps);bool StackEmpty(ST* ps);
Stack.c
#include "Stack.h"void StackInit(ST* ps)
{assert(ps);ps->a = (STDataType*)malloc(sizeof(STDataType) * 4);if (ps->a == NULL){printf("malloc fail\n");exit(-1);}ps->capacity = 4;ps->top = 0;
}void StackDestory(ST* ps)
{assert(ps);free(ps->a);ps->a = NULL;ps->top = ps->capacity = 0;
}// 入栈
void StackPush(ST* ps, STDataType x)
{assert(ps);// 满了-》增容if (ps->top == ps->capacity){STDataType* tmp = (STDataType*)realloc(ps->a, ps->capacity * 2 * sizeof(STDataType));if (tmp == NULL){printf("realloc fail\n");exit(-1);}else{ps->a = tmp;ps->capacity *= 2;}}ps->a[ps->top] = x;ps->top++;
}// 出栈
void StackPop(ST* ps)
{assert(ps);// 栈空了，调用Pop，直接中止程序报错assert(ps->top > 0);//ps->a[ps->top - 1] = 0;ps->top--;
}STDataType StackTop(ST* ps)
{assert(ps);// 栈空了，调用Top，直接中止程序报错assert(ps->top > 0);return ps->a[ps->top - 1];
}int StackSize(ST* ps)
{assert(ps);return ps->top;
}bool StackEmpty(ST* ps)
{assert(ps);return ps->top == 0;
}

二 .队列

1 队列的概念及结构

队列也是一种特殊的线性表，队列中的元素及元素间的逻辑关系和线性表完全相同，在操作上的差异是; 线性表允许在任意位置插入和删除元素。而队列只允许在其一端进行插入操作，在其另一端进行删除操作。

在队列中，允许进行插入操作的一端成为队尾。允许进行删除操作的一端成为队头，队头队尾，分别由队头指针和队尾指针指示。队列的插入操作通常称作入队列，队列的删除操作通常称作出队列，根据队列的定义，我们可以把，队列想象成是一种先进先出的线性表，简称先进先出表

 

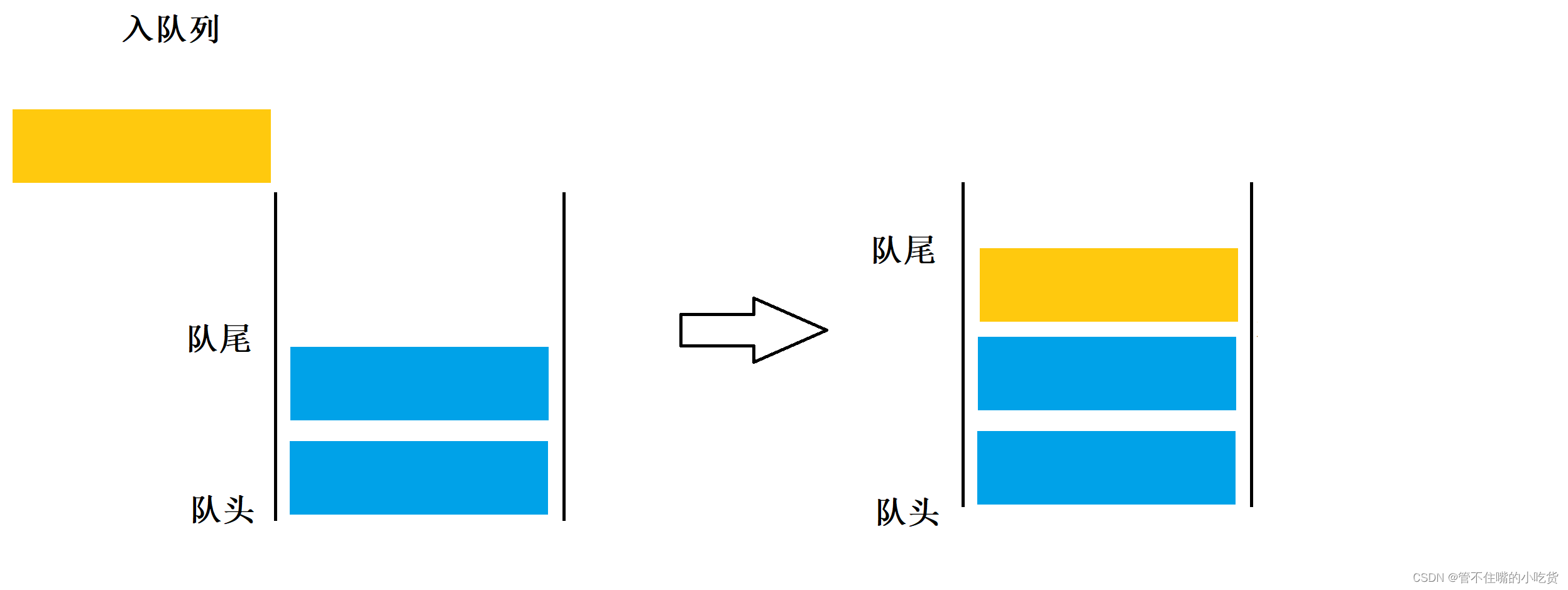
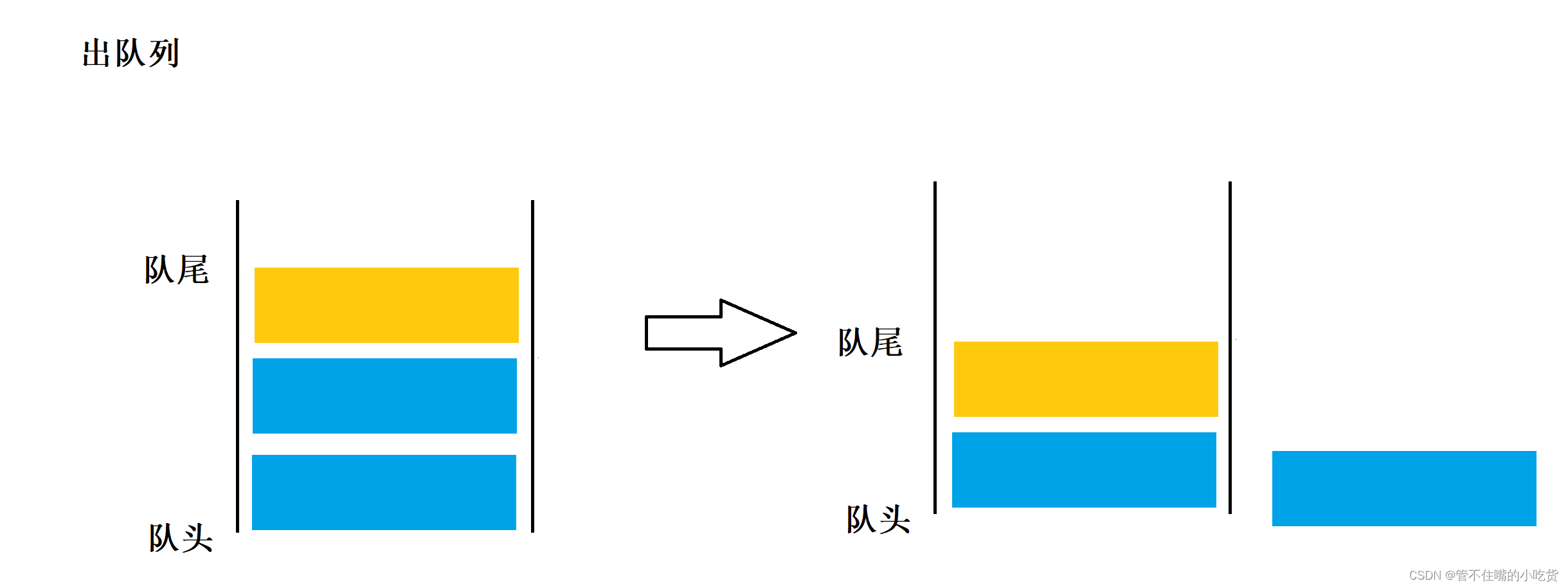
2 队列的实现形式

队列也可以数组和链表的结构实现，但使用链表的结构实现更优一些，因为如果使用数组的结构， 出队列在数组头上出数据，效率会比较低。

3 队列的操作实现

3.1  结构体
typedef int QDataType;typedef struct QueueNode
{struct QueueNode* next;QDataType data;
}QNode;typedef struct Queue
{QNode* head;QNode* tail;
}Queue;
3.2  队列初始化
void QueueInit(Queue* pq)
{assert(pq);pq->head = pq->tail = NULL;
}
3.3  队列的销毁
void QueueDestory(Queue* pq)
{assert(pq);QNode* cur = pq->head;while (cur){QNode* next = cur->next;free(cur);cur = next;}pq->head = pq->tail = NULL;
}
3.4  入队列（队尾入）
// 队尾入
void QueuePush(Queue* pq, QDataType x)
{assert(pq);QNode* newnode = (QNode*)malloc(sizeof(QNode));if (newnode == NULL){printf("malloc fail\n");exit(-1);}newnode->data = x;newnode->next = NULL;if (pq->tail == NULL){pq->head = pq->tail = newnode;}else{pq->tail->next = newnode;pq->tail = newnode;}
}
 3.5  出队列（队头出）
// 队头出
void QueuePop(Queue* pq)
{assert(pq);assert(pq->head);if (pq->head->next == NULL){free(pq->head);pq->head = pq->tail = NULL;}else{QNode* next = pq->head->next;free(pq->head);pq->head = next;}
}
3.6  删除队内数据
3.6.1  前删
QDataType QueueFront(Queue* pq)
{assert(pq);assert(pq->head);return pq->head->data;
}
3.6.2  尾删
QDataType QueueBack(Queue* pq)
{assert(pq);assert(pq->head);return pq->tail->data;
}
3.7  返回队列大小
int QueueSize(Queue* pq)
{assert(pq);int size = 0;QNode* cur = pq->head;while (cur){++size;cur = cur->next;}return size;
}
3.8  清空队列 
bool QueueEmpty(Queue* pq)
{assert(pq);return pq->head == NULL;
}

4 完整代码

queue.h:
#define _CRT_SECURE_NO_WARNINGS
#pragma once#include <stdio.h>
#include <stdbool.h>
#include <assert.h>
#include <stdlib.h>
typedef int QDataType;typedef struct QueueNode
{struct QueueNode* next;QDataType data;
}QNode;typedef struct Queue
{QNode* head;QNode* tail;
}Queue;//队列初始化
void QueueInit(Queue* pq);//队列销毁
void QueueDestory(Queue* pq);// 队尾入
void QueuePush(Queue* pq, QDataType x);// 队头出
void QueuePop(Queue* pq);//前删
QDataType QueueFront(Queue* pq);//后删
QDataType QueueBack(Queue* pq);//队列大小
int QueueSize(Queue* pq);//清空队列
bool QueueEmpty(Queue* pq);
queue.c:
#define _CRT_SECURE_NO_WARNINGS
#include "Queue.h"void QueueInit(Queue* pq)
{assert(pq);pq->head = pq->tail = NULL;
}void QueueDestory(Queue* pq)
{assert(pq);QNode* cur = pq->head;while (cur){QNode* next = cur->next;free(cur);cur = next;}pq->head = pq->tail = NULL;
}// 队尾入
void QueuePush(Queue* pq, QDataType x)
{assert(pq);QNode* newnode = (QNode*)malloc(sizeof(QNode));if (newnode == NULL){printf("malloc fail\n");exit(-1);}newnode->data = x;newnode->next = NULL;if (pq->tail == NULL){pq->head = pq->tail = newnode;}else{pq->tail->next = newnode;pq->tail = newnode;}
}// 队头出
void QueuePop(Queue* pq)
{assert(pq);assert(pq->head);if (pq->head->next == NULL){free(pq->head);pq->head = pq->tail = NULL;}else{QNode* next = pq->head->next;free(pq->head);pq->head = next;}
}QDataType QueueFront(Queue* pq)
{assert(pq);assert(pq->head);return pq->head->data;
}QDataType QueueBack(Queue* pq)
{assert(pq);assert(pq->head);return pq->tail->data;
}int QueueSize(Queue* pq)
{assert(pq);int size = 0;QNode* cur = pq->head;while (cur){++size;cur = cur->next;}return size;
}bool QueueEmpty(Queue* pq)
{assert(pq);return pq->head == NULL;
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.mzph.cn/news/157944.shtml

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

springboot+jsp+bootstrap+java问卷调查系统

springboot+jsp+bootstrap+java问卷调查系统

系统功能需求包含业务需求和功能需求&#xff0c;系统功能需求分析是在了解用户习惯、开发人员技术和实力等各个因素的前提下&#xff0c;对其进行深入分析&#xff0c;了解系统基本需求后&#xff0c;基本功能如下&#xff1a; 本课题要求实现优质的问卷调查系统&#xff0c;就…
阅读更多...
安全框架springSecurity+Jwt+Vue-2(后端开发)

安全框架springSecurity+Jwt+Vue-2(后端开发)

一、创建项目及配置 ①&#xff1a;创建新的项目及常用包 ②&#xff1a;引入依赖和配置 devtools&#xff1a;项目的热加载重启插件 <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-web</artifactId&…
阅读更多...
如何配置ESB单据集成接口

如何配置ESB单据集成接口

ESB企业服务总线在实际项目中主要用于各业务系统之间的集成&#xff0c;集成包括数据集成、应用集成以及业务单据集成等&#xff0c;ESB企业服务总线主要包含三部分&#xff1a;ESB设计器、SMC管理控制台以及Server运行环境&#xff0c;ESB设计器用于服务以及集成流程的开发&am…
阅读更多...
【C++ 设计模式】面向对象设计原则 Template Method 模式 Strategy 策略模式

【C++ 设计模式】面向对象设计原则 Template Method 模式 Strategy 策略模式

一、面向对象设计原则 重新认识面向对象 理解隔离变化 • 从宏观层面来看&#xff0c;面向对象的构建方式更能适应软件的变化&#xff0c; 能将变化所带来的影响减为最小 各司其职 • 从微观层面来看&#xff0c;面向对象的方式更强调各个类的“责任” • 由于需求变化导…
阅读更多...
Tesco EDI需求分析

Tesco EDI需求分析

Tesco&#xff0c;成立于1919年&#xff0c;是一家全球领先的综合性零售企业&#xff0c;总部位于英国。公司致力于提供高质量、多样化的商品和服务&#xff0c;以满足客户的需求。Tesco的使命是通过创新和卓越的客户服务&#xff0c;为客户创造更美好的生活。多年来&#xff0…
阅读更多...
vue2.x源码刨析-new Vue的时候做了什么(手写简易版01)

vue2.x源码刨析-new Vue的时候做了什么(手写简易版01)

本篇文章大致的介绍一下new Vue的过程&#xff0c; 首先我们在生成一个Vue实例化对象的时候&#xff0c;一般会这样写&#xff1a; <div id"app" style"color: red">{{name}} dep {{age}} dep {{name}}</div> const vm new Vue({data() {ret…
阅读更多...
【idea】解决idea 执行maven build总下载 Downloading maven-metadata.xml文件

【idea】解决idea 执行maven build总下载 Downloading maven-metadata.xml文件

可以看到如下日志中打印了执行的命令行&#xff0c;其中包含 --update-snapshots&#xff0c;是强制更新的意思。 日志内容如下&#xff1a; D:\env\jdk1.8.0_261\bin\java.exe --update-snapshots -s D:\env\apache-maven-3.8.6\conf\settings.xml -Dmaven.repo.localD:\env\…
阅读更多...
【开源】基于Vue.js的天然气工程业务管理系统的设计和实现

【开源】基于Vue.js的天然气工程业务管理系统的设计和实现

项目编号&#xff1a; S 021 &#xff0c;文末获取源码。 \color{red}{项目编号&#xff1a;S021&#xff0c;文末获取源码。} 项目编号&#xff1a;S021&#xff0c;文末获取源码。 目录 一、摘要1.1 项目介绍1.2 项目录屏 二、功能模块三、使用角色3.1 施工人员3.2 管理员 四…
阅读更多...
tomcat （SCI）ServletContainerInitializer 的加载原理

tomcat （SCI）ServletContainerInitializer 的加载原理

问题&#xff1a;使用WebScoket的时候发现通过ServerEndpoint方式注册上去的url无法访问&#xff0c;报错404 经过排查发现在WsServerContainer这个类中的addEndpoint方法一直没有触发ServerEndpoint注解的扫描 通过该方法来源于StandardContext.startInternal()方法的调用如下…
阅读更多...
CSS特效015：7个小球转圈圈加载效果

CSS特效015：7个小球转圈圈加载效果

CSS常用示例100专栏目录 本专栏记录的是经常使用的CSS示例与技巧&#xff0c;主要包含CSS布局&#xff0c;CSS特效&#xff0c;CSS花边信息三部分内容。其中CSS布局主要是列出一些常用的CSS布局信息点&#xff0c;CSS特效主要是一些动画示例&#xff0c;CSS花边是描述了一些CSS…
阅读更多...
ERP对接淘宝/天猫/京东/拼多多商品详情数据API接口

ERP对接淘宝/天猫/京东/拼多多商品详情数据API接口

引言 今天&#xff0c;我们时代变化非常快&#xff0c;传统行业做法&#xff0c;已经无法完全适应时代的发展。互联网的发展&#xff0c;造成了一股网购热。京东&#xff0c;天猫&#xff0c;淘宝&#xff0c;易购……网购&#xff0c;给我们生活带来了方便&#xff0c;消费者…
阅读更多...
axios封装使用

axios封装使用

&#x1f33c;未封装 在项目中往往一个页面存在着要联调好几个接口&#xff0c;此时用下面的写法就会显得代码很冗余 // 向给定ID的用户发起请求 axios.get(/user?ID123456,{ params: { //发送请求的数据ID: 123456 } }) .then(function (response) { // 处理成功情…
阅读更多...
人工智能：科技之光，生活之美

人工智能：科技之光，生活之美

在科技飞速发展的今天&#xff0c;人工智能已经深入到我们的生活中&#xff0c;它如同一束璀璨的科技之光&#xff0c;照亮我们生活的每一个角落&#xff0c;使我们的生活更加美好。下面我将从人工智能的领域、应用以及对人工智能的看法三个方面来谈谈它对我们生活的影响。 一、…
阅读更多...
最新红盟云卡个人自动发卡开源系统源码+全开源无加密+虚拟商品在线售卖平台

最新红盟云卡个人自动发卡开源系统源码+全开源无加密+虚拟商品在线售卖平台

源码简介&#xff1a; 最新红盟云卡个人自动发卡开源系统源码全开源无加密虚拟商品在线售卖平台&#xff0c;支持多个接口的个人免签功能。 红盟云卡系统是一款基于PHP和MySQL开发的虚拟商品在线售卖平台。它具备美观且功能丰富的发卡网站特性&#xff0c;并可与社区进行无缝…
阅读更多...
【量化】一个简版单档tick数据回测框架

【量化】一个简版单档tick数据回测框架

这是一个简易的模拟实际交易流程的回测框架&#xff0c;所使用的行情数据是单档的tick成交数据。为了实现调用者可以实现自己的交易逻辑&#xff0c;本框架预留了几个函数予以调用者能够继承类后在子类中重写以实现买入卖出信号的生成&#xff08;check_sell()和check_buy()&am…
阅读更多...
Docker Swarm总结

Docker Swarm总结

1、swarm 理论基础 1.1 简介 Docker Swarm 是由 Docker 公司推出的 Docker 的原生集群管理系统&#xff0c;它将一个 Docker 主机池变成了一个单独的虚拟主机&#xff0c;用户只需通过简单的 API 即可实现与 Docker 集群的通 信。Docker Swarm 使用 GO 语言开发。从 Docker 1.…
阅读更多...
inf和nan

inf和nan

在某些编程语法中inf表示无穷大,nan表示不是一个数(not a number) nan表示这个数不确定,而无穷大表示这个数任意大 1/0inf 这里把0当做一个无限接近0,但是非0的数 5-inf-inf 一个数减去无穷大会等于负无穷大 而inf-infnan 因为两个无穷大相减有很多可能,可能等于一个常数,也可能…
阅读更多...
Linux find命令

Linux find命令

根据时间查找 ## 查找几分钟之内创建的文件 find . -cmin 5
阅读更多...
HTML所有功能大汇总

HTML所有功能大汇总

HTML所有的功能&#xff0c;都在下面的表格中呈现清楚了。千万不要死记硬背&#xff0c;但是在遇到困难的时候&#xff0c;可以按照这个表进行查找。 类别功能HTML标签文本样式粗体<b></b> 或 <strong></strong>斜体<i></i>或<em>&…
阅读更多...
Ajax基础（应用场景｜jquery实现Ajax｜注意事项｜Ajax发送json数据｜Ajax携带文件数据）

Ajax基础（应用场景｜jquery实现Ajax｜注意事项｜Ajax发送json数据｜Ajax携带文件数据）

文章目录 一、Ajax简介二、基于jquery实现Ajax三、使用Ajax注意的问题1.Ajax不要与form表单同时提交2.后端响应格式问题3、使用了Ajax作为请求后的注意事项 四、前后端数据传输的编码格式(content-Type)1.urlencoded2.formdata3.application/json 五、Ajax携带文件数据六、Ajax…
阅读更多...
最新文章

Copyright @ 2022~2023