1. 题目链接:LCR 091. 粉刷房子
2. 题目描述:
假如有一排房子,共
n个,每个房子可以被粉刷成红色、蓝色或者绿色这三种颜色中的一种,你需要粉刷所有的房子并且使其相邻的两个房子颜色不能相同。当然,因为市场上不同颜色油漆的价格不同,所以房子粉刷成不同颜色的花费成本也是不同的。每个房子粉刷成不同颜色的花费是以一个
n x 3的正整数矩阵costs来表示的。例如,
costs[0][0]表示第 0 号房子粉刷成红色的成本花费;costs[1][2]表示第 1 号房子粉刷成绿色的花费,以此类推。请计算出粉刷完所有房子最少的花费成本。
示例 1:
输入: costs = [[17,2,17],[16,16,5],[14,3,19]] 输出: 10 解释: 将 0 号房子粉刷成蓝色,1 号房子粉刷成绿色,2 号房子粉刷成蓝色。最少花费: 2 + 5 + 3 = 10。示例 2:
输入: costs = [[7,6,2]] 输出: 2提示:
costs.length == ncosts[i].length == 31 <= n <= 1001 <= costs[i][j] <= 20
3. 解法(动态规划):
3.1 算法思路:
- 状态表示:
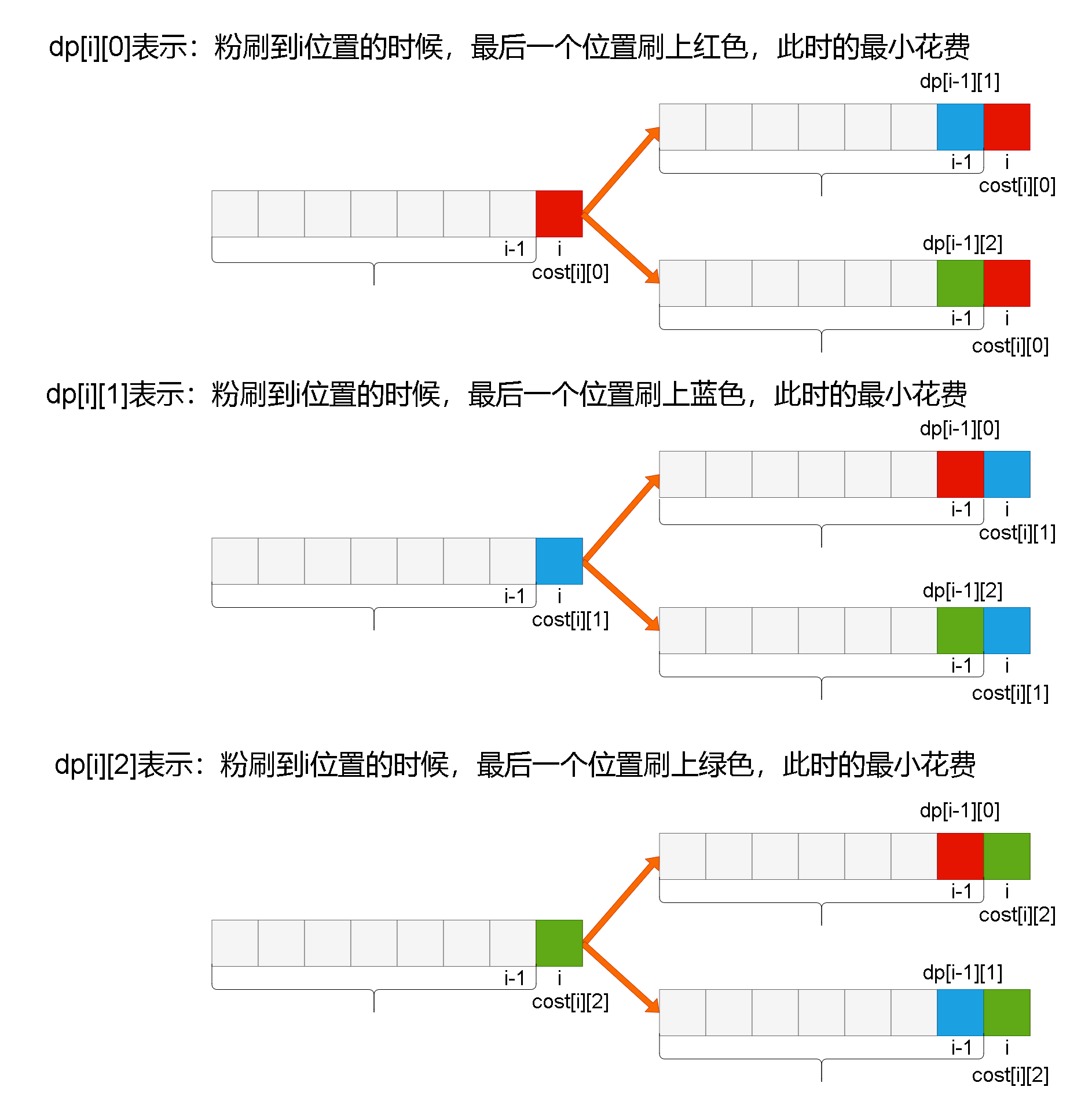
dp[i][0]表示:粉刷到i位置的时候,最后一个位置粉刷上红色,此时的最小花费
dp[i][1]表示:粉刷到i位置的时候,最后一个位置粉刷上蓝色,此时的最小花费
dp[i][2]表示:粉刷到i位置的时候,最后一个位置粉刷上绿色,此时的最小花费
- 状态转移方程:
如果第i个位置粉刷上红色,那么i-1 上可以是蓝色或者绿色。dp[i][0] = min(dp[i - 1][1], dp[i - 1][2]) + costs[i - 1][0];
如果第i个位置粉刷上蓝色,那么i-1 上可以是红色或者绿色。dp[i][1] = min(dp[i - 1][0], dp[i - 1][2]) + costs[i - 1][1];
如果第i个位置粉刷上绿色,那么i-1 上可以是红色或者蓝色。dp[i][2] = min(dp[i - 1][1], dp[i - 1][0]) + costs[i - 1][2];
- 初始化:
可以在最前面加上一个辅助节点,帮助我们初始化,使用这种技巧要注意两个点:
赋值结点里面的值要保证后续填表是正确的
下标的映射关系
- 填表顺序:
根据动态转移方程得,从左往右,三个表一起填
- 返回值:
根据状态表示,应该返回最后一个位置粉刷上三种颜色情况下的最小值,因此需要返回 min(dp[n][0], min(dp[n][1], dp[n][2]));
3.2 C++算法代码:
class Solution {
public:int minCost(vector<vector<int>>& costs) {// 获取costs的行数int n = costs.size();// 初始化dp数组,大小为n+1行,3列vector<vector<int>> dp(n + 1, vector<int>(3));// 遍历每一行for (int i = 1; i <= n; i++) {// 计算第i行的最小花费,分别对应三种颜色dp[i][0] = min(dp[i - 1][1], dp[i - 1][2]) + costs[i - 1][0];dp[i][1] = min(dp[i - 1][0], dp[i - 1][2]) + costs[i - 1][1];dp[i][2] = min(dp[i - 1][1], dp[i - 1][0]) + costs[i - 1][2];}// 返回最后一行中三种颜色的最小花费return min(dp[n][0], min(dp[n][1], dp[n][2]));}
};




流程详解及acquire方法总结)



))

)
)







)