seismicunix基础-声波波动方程推导
接触波动方程的研究人员都绕不开这个公式,这是在一维状态下波动方程
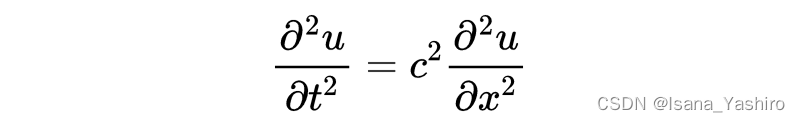
但是对于这个方程是怎样来的很少有人能说清楚,其中涉及到牛顿第二运动定律,物体的加速度与受到的力有关。
假设一维弦是大量紧密连接的质点,某个质点受力开始震动后,附近的质点无损耗地将这个力传导出去,由此造成了弦有规律地振动。
首先我们可以假设在原点处的质点受力开始震动,在t时刻时其振幅值为y=f(t),该振动以速度v向x轴方向传播,那么在t时刻距原点x位置处的质点振幅值为f(t-x/v),x处的振动比原点慢x/v时间。
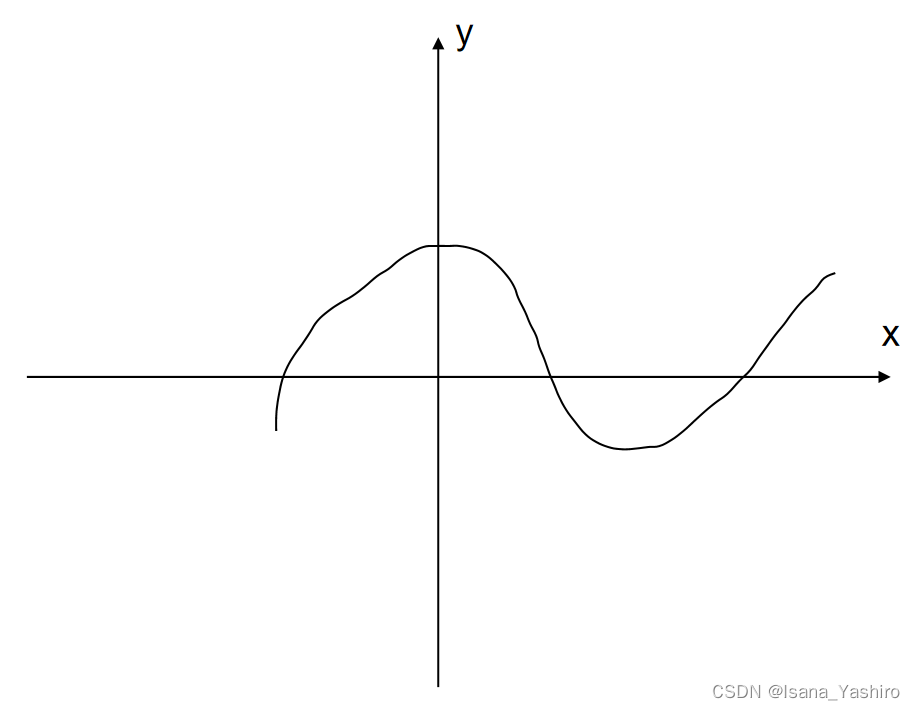
用一个函数u(x,t)来表示弦上任意位置质点在任意时刻的振幅值,那么我们可以得到

令z=t-x/v,对方程关于t求一阶偏导,可以得到
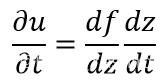
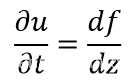
对方程关于t求二阶偏导

对方程关于x求一阶偏导,可以得到
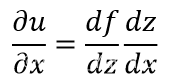

对方程关于x求二阶偏导,
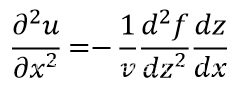
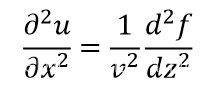
将方程关于时间t和位置x的二阶导方程联立,可得

由此得到开头的齐次方程。
将该方程推广至二维,一维弦由单个质点紧密连接形成,二维膜则由平面上平铺的质点紧密形成,膜上某点受力振动后周围的点由于牛顿第二运动定律的作用,会将振动传导出去,由此造成膜的震动。
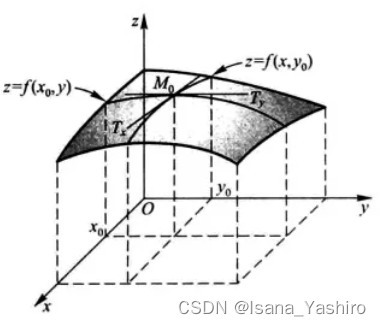
同样的,我们可以假设膜在原点处的质点受力开始震动,在t时刻时其振幅值为amp=f(t),该振动以速度v向xy平面内传播,那么在t时刻距原点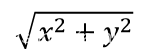 位置处的质点振幅值为
位置处的质点振幅值为 ,该处的振动比原点慢
,该处的振动比原点慢 时间。
时间。
用一个函数u(x,y,t)来表示膜上任意位置质点在任意时刻的振幅值,那么我们可以得到

对方程分别关于时间t,空间x,y求二阶偏导,可得

推广至三维,则可以得到三维波动方程



 音频篇 上)

:三次握手和四次挥手分析和SIGPIPE信号的处理)


)








的攻击流程与防御措施)


