系列文章目录
什么是计算机网络?
什么是网络协议?
计算机网络的结构
数据交换之电路交换
数据交换之报文交换和分组交换
分组交换 vs 电路交换
计算机网络性能(1)——速率、带宽、延迟
计算机网络性能(2)——时延带宽积、丢包率、吞吐量/率
计算机网络体系结构概念
OSI参考模型基本概念
OSI参考模型中非端-端层(物理层、数据链路层、网络层)功能介绍
OSI参考模型中端-端层(传输层、会话层、表示层、应用层)功能介绍
TCP/IP参考模型基本概念,包括五层参考模型
网络应用的体系结构
网络应用进程通信
网络应用对传输服务的需求
Web应用之HTTP协议(涉及HTTP连接类型和HTTP消息格式)
Cookie技术
Web缓存/代理服务器技术
传输层服务概述、传输层 vs. 网络层
传输层——多路复用和多路分用
传输层——UDP简介
传输层——可靠数据传输原理之Rdt协议
传输层——可靠数据传输之流水线机制与滑动窗口协议
传输层——TCP特点与段结构
传输层——TCP的可靠数据传输
TCP连接管理(图解三次握手和四次挥手)
传输层——拥塞控制原理与解决方法
TCP的拥塞控制机制
网络层服务与核心功能
网络层服务模型——虚电路网络
网络层服务模型——数据报网络
Internet网络的网络层——IP协议之IP数据报的结构
IP分片
IP编址与有类IP地址
IP子网划分与子网掩码
CIDR与路由聚合
DHCP协议
网络地址转换(NAT)
ICMP(互联网控制报文协议)
IPv6简介
路由算法之链路状态路由算法
- 系列文章目录
- 说明
- 示例
说明
距离向量路由算法基于Bellman-Ford方程(动态规划)。

在这样的基础上,作为x结点,其实并不需要知道整个网络拓扑,它只需要知道和邻居v之间直接链路的费用和邻居v到目的y的最短路径的费用就可以知道通过哪个邻居可以获得到达目的结点y的最小路径费用。
下面看一个例子:
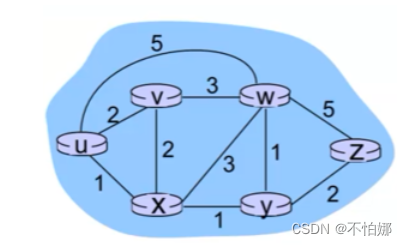
u有三个邻居:v、z、w

u不需要获取整个路径,只需要获取最短路径的下一跳,这个信息用于转发表中。
距离向量路由算法需要很多次迭代才能得到dx (y) 。所以在很长一段时间的计算过程中,使用Dx (y) 即从结点x到结点y的最小费用估计,经过很多次计算之后可能会趋向于dx (y) 。x维护距离向量(DV): Dx = [Dx (y): y є N ]。x还需要维护到达每个邻居的费用 c(x,v)和其所有邻居的距离向量: Dv = [Dv (y): y є N ]。
核心思想就是:
- 每个结点不定时地将其自身的DV估计发送给其邻居
- 当x接收到邻居的新的DV估计时,即依据B-F更新其自身的距离向量估计:Dx (y) ← minv {c(x,v) + Dv (y)} for each node y ∊ N
- Dx (y)将最终收敛于实际的最小费用 dx (y)
距离向量路由算法有几个特点:
- 异步迭代:每一个路由器并不是同步迭代、同步结束。引发每次局部迭代的因素主要是:局部链路费用改变、来自邻居的DV更新
- 分布式:每个结点只当DV变化时才通告给邻居。邻居在必要时(其DV更新后发生改变)再通告它们的邻居
根据这些特点,距离向量路由算法的基本描述如下所示:
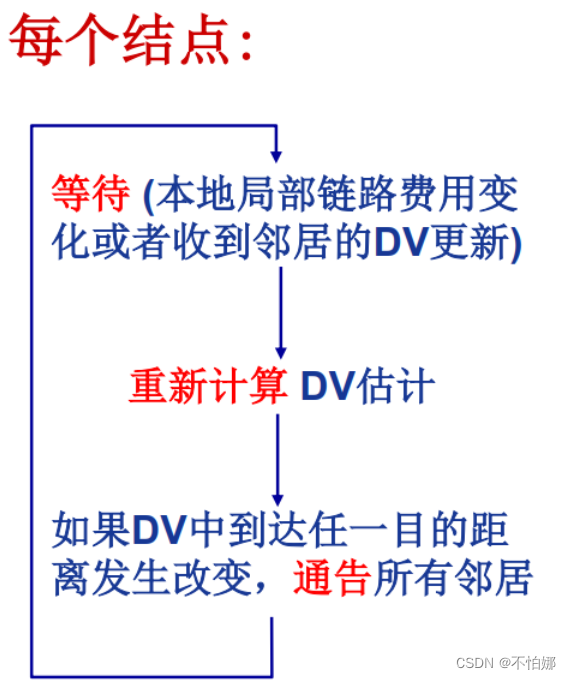
示例
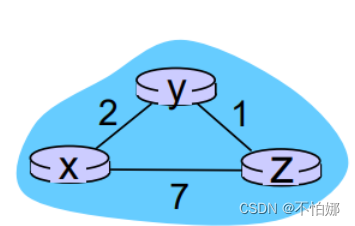
首先初始化估计向量。并且此时它们的邻居结点的向量并没有交换过来,所以都是∞。
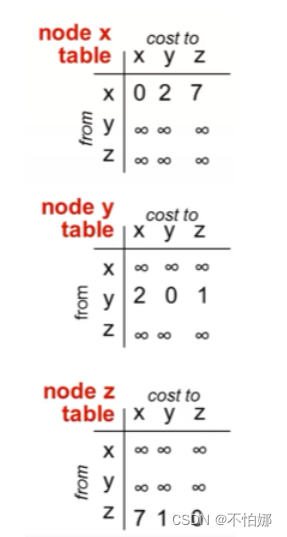
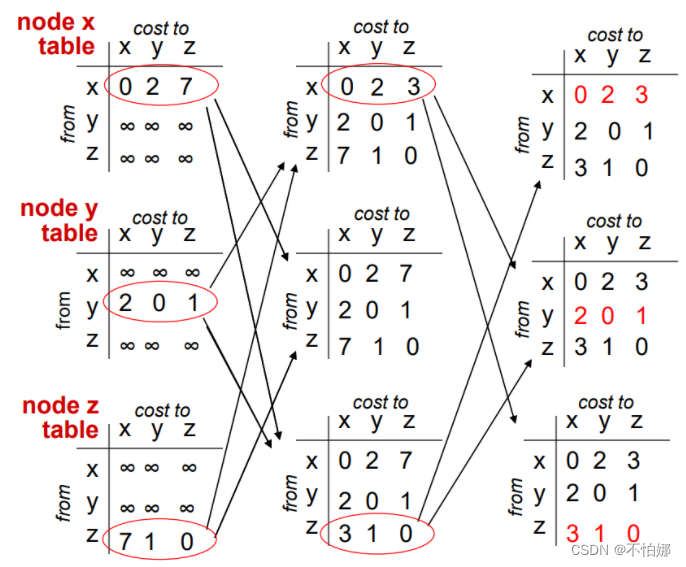
然后交换邻居结点的距离向量,然后重新计算它到达不同结点的最小费用。
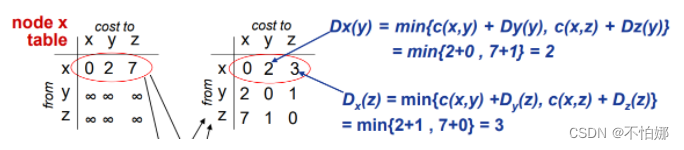
重新计算之后如果有变化需要重新交换给邻居。







的攻击流程与防御措施)











