利用SVD对图像进行压缩
使用SVD能够对数据进行降维,对图像进行SVD,降维之后然后重构数据,还原后的图像就是压缩后的图像。
SVD

SVD进行图像压缩所依据的数学原理就是矩阵的近似表示:
A m × n ≈ U m × k ∑ k × k V k × n T A_{m\times n}\approx U_{m\times k}{\sum}_{k\times k}V_{k\times n}^T Am×n≈Um×k∑k×kVk×nT
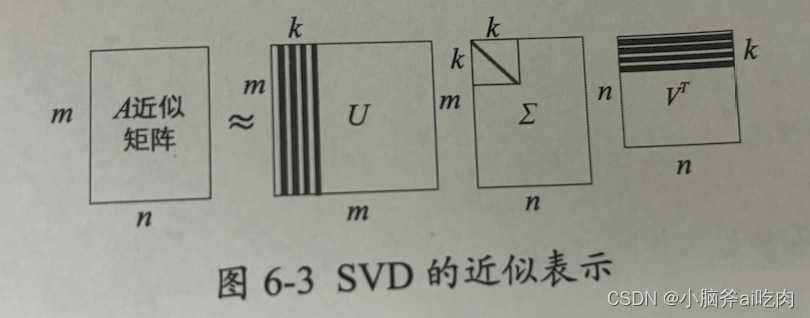
使用SVD对图像进行压缩的最关键的就是确定k值,也就是使用多少个奇异值。用的越多那肯定包含原矩阵的信息就越多,但这样处理的数据也多,所以需要在数据量和还原度之间取个平衡。确定k有很多启发式的策略,其中一个典型的做法就是保留矩阵中90%的能量信息,即计算所有奇异值的平方和,取前k个奇异值平方和是总体奇异值平方和的90%。另一个启发式策略是当矩阵有上万奇异值时,就保留前面的2000或3000个,该方法虽然在实际中容易实施,但是任何数据集都不能保证前3000个奇异值就能够包含90%的能量信息。
在进行图像压缩时,我们采用两种策略来确定k的值:
1.通过奇异值总和的百分比来确定k的值
2.通过奇异值总个数的百分比来确定k的值
from PIL import Image
import numpy as npdef get_approx_SVD1(data, percent):#这里了的percent是奇异值总和的百分比U, s, VT = np.linalg.svd(data)Sigma = np.zeros(np.shape(data))Sigma[:len(s), :len(s)] = np.diag(s)count = int(sum(s)) * percentk = -1curSum = 0while curSum <= count:k += 1curSum += s[k]D = U[:, :k].dot(Sigma[:k, :k].dot(VT[:k, :]))#将矩阵 D 中小于 0 的元素设置为 0,将大于 255 的元素设置为 255。#因为在图像处理中,像素值通常被限制在0~255D[D < 0] = 0D[D > 255] = 255return np.rint(D).astype("uint8")def get_approx_SVD2(data, percent):U, s, VT = np.linalg.svd(data)Sigma = np.zeros(np.shape(data))Sigma[:len(s), :len(s)] = np.diag(s)k = (int)(percent * len(s))D = U[:, :k].dot(Sigma[:k, :k].dot(VT[:k, :]))D[D < 0] = 0D[D > 255] = 255return np.rint(D).astype("uint8")def rebuild_img(filename, p, get_approx_SVD, flag):img = Image.open(filename, 'r')a = np.array(img)#以下的R0,G0,B0,R,G,B都是二维的,不要想成三维了R0 = a[:, :, 0]#获得红色的色素值G0 = a[:, :, 1]#获得绿色的色素值B0 = a[:, :, 2]#获得蓝色的色素值R = get_approx_SVD(R0, p)G = get_approx_SVD(G0, p)B = get_approx_SVD(B0, p)I = np.stack((R, G, B), 2)#合成三通道的Nummpy数组#Image.fromarray()函数的作用是将Nummpy数组还原为图像对象Image.fromarray(I).save(str(p * 100) + flag + ".jpg")img = Image.open(str(p * 100) + flag + ".jpg", 'r')img.show()filename = "./test.jpg"
'''
np.arange(0.2, 1.2, 0.2)
第一个参数(0.2):起始值,即数组的第一个元素。
第二个参数(1.2):终止值,创建的数组中不包括这个值。
第三个参数(0.2):步长,即数组中相邻元素之间的差值。
[0.2,0.4,0.6,0.8,1.0]
'''
for p in np.arange(0.2, 1.2, 0.2):rebuild_img(filename, p, get_approx_SVD1, "SVD1")
for p in np.arange(0.2, 1.2, 0.2):rebuild_img(filename, p, get_approx_SVD2, "SVD2")原图:

效果示例:

使用特征值可以将图像进行压缩处理,压缩后的图像颜色像素会损失部分,通过设定不同的奇异值筛选百分比,对比图片压缩后的效果。
原图像的每一层大小为512x512=262144,效果图中上层的5个图,依次对应按奇异值总和的20%,40%,60%,80%,100%,进行压缩,当按奇异值总和的60%压缩时,可以达到原图像的效果,此时,只取了33个奇异值(占总奇异值个数的6%),即 U U U、 ∑ \sum ∑、 V T V^T VT的大小分别为512x33、33x33、33x512。此时,大小总共为 512 × 33 + 33 × 33 + 33 × 512 = 34881 512\times33+33\times33+33\times512=34881 512×33+33×33+33×512=34881,3个矩阵的大小总和远小于原图像的每一层大小。效果图下层的5个图,依次按照奇异值个数的20%,40%,60%,80%,100%,进行压缩。显然,当按照奇异值个数的20%取值时,其对应的奇异值总和的百分比已经超过了60%(算一下)。因此,建议按照奇异值总和的百分比压缩图像(其实通俗来说就是用的数据少,但是效果还不错,下层的图效果虽然都很好,但是用的数据太多了,压缩的数据量不够大)


![[Docker]八.Docker 容器跨主机通讯](http://pic.xiahunao.cn/[Docker]八.Docker 容器跨主机通讯)


:Linux 磁盘与文件管理系统)













