二 实例
1.
\Delta_{w}=\frac{\partial l}{\partial w_{i+1}}weight:\frac{\partial l}{\partial x_{i+1}}
效果如下
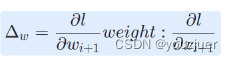
其中对于希腊字母的大小写来说，可以参考：
【LaTeX 语法】字母表示 ( 大写、小写、异体 希腊字母 | 粗体字母 | 花体字母 )_latex字母_韩曙亮的博客-CSDN博客
https://blog.csdn.net/shulianghan/article/details/122977227
