在Google paly应用上架的过程中,相信大多数开发者都遇到过开发者账号因为关联问题,导致应用包被拒审和封号的情况。
而众所周知,开发者账号注册或登录的IP地址及设备是造成账号关联的重要因素之一。酷鸟云最新上线的原生IP能有效降低账号因IP问题而关联的风险,助力提高谷歌上架成功率!
与普通IP相比,原生静态住宅IP有哪些优势?为什么可以降低账号关联风险?
①归属地一致:原生IP是在运营商的中央机房部署的,与普通宽带业务场景共用机房。也就是说开发者们可以最大程度地模拟真实的海外用户环境,从而提高了账号的可信度。
以纽约为例,IP地址可以精准定位到纽约具体区域(例如华盛顿)。同时,实测表明,在谷歌平台的归属地与其他平台判断都非常准确。
②IP数量丰富:原生IP地址数量众多。以美国为例,38.0.0.0/8的IP地址,包含了超过1500万个IP。数量庞大,使得平台无法通过C段对IP进行大批量关联,从而有效降低了账号因为其他用户违规操作或者其他地址违规操作导致整个IP池被封的风险。
③更安全:原生IP可以提供运营商ASN信息,这意味着每个IP都与特定的运营商相关联,类似中国电信、移动、联通。平台就难以通过C段和ASN进行双重定位封杀整个云厂商的IP池,提供更安全更真实的网络环境。
④避免了IP滥用:原生IP是从运营商直采而来的,避免了普通云平台回收再重复利用而导致上一个IP还未被谷歌解除限制,就马上被新用户采购导致IP滥用的情况发生。这样一来,开发者们就不必担心因为使用了被滥用的IP而可能因此被平台误判为滥用账号了。
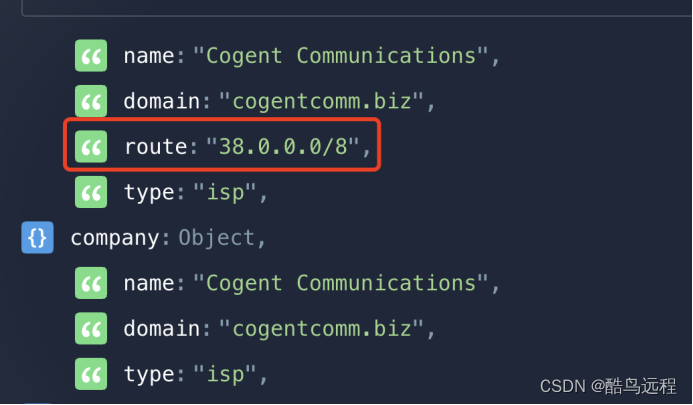
(ipinfo.io具体属性)
此外,最近香港IP能够减少水电账单出现已经得到充分验证,用户购买香港IP注册谷歌均不需要对个人号提供二次验证。
企业号可以解决8.3/10.3账号关联问题?
除了推荐使用原生IP,同时建议使用企业号来进行上架,目前个人号风控比较严重,并且后续要推出个人号上线应用需要邀请测试的情况。
虽然我们不知道谷歌对企业号后续会有什么新的计划或策略,但根据近期大部分开发者真金白银的测试和反馈,企业号能有效解决账号频繁因8.3/10.3关联被封的问题,比个人号上架成功率更高、包的在线时间更长。
且按照谷歌的规定,注册企业开发者账号,需要邓氏编码才能注册成功和发布应用。邓氏编码是具有唯一性的9位数标识符,由 Dun & Bradstreet 分配给各组织公司,用于验证商家,一个公司可免费申请一个。
也就是说,企业号的注册门槛更高,需要提供的证明文件更多,更能够证明应用的合法性和可信度,也就更容易通过审核。
无论后续企业号是否因为大批量的注册上架行为导致产生新的风控,目前来说可以短暂的度过这次个人号风控,能够正常的运营包。
此外,根据Google play最新政策,2023.11.13之后注册的个人开发者账号,必须让至少20名测试人员连续14天参与符合Google要求的封闭测试,才能申请发布正式版应用。
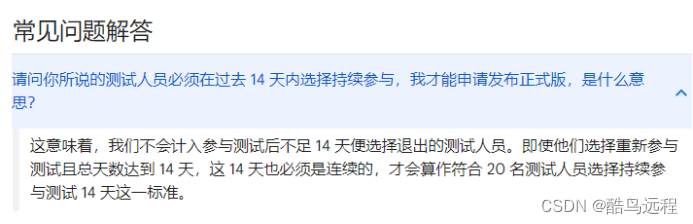
针对该项业务,酷鸟云推出云手机,目前经过实测通过云手机直接注册的谷歌账号可以跳过手机验证码,并且在留评环节有优异表现。持续实测下来,完全满足谷歌对环境的要求,做到最大程度模拟真实手机用户,后续会输出云手机的详细介绍以及使用技巧。
以上是近期谷歌热点,根据谷歌现在越来越严格的风险控制,建议开发者们使用企业号和原生IP相结合,降低账号关联风险,提高上架成功率。
 — Informer源码详解与运行)


















)