论文笔记--GloVe: Global Vectors for Word Representation
- 1. 文章简介
- 2. 文章概括
- 3 文章重点技术
- 3.1 两种常用的单词向量训练方法
- 3.2 GloVe
- 3.3 模型的复杂度
- 4. 文章亮点
- 5. 原文传送门
- 6. References
1. 文章简介
- 标题:GloVe: Global Vectors for Word Representation
- 作者:Jeffrey Pennington, Richard Socher, Christopher D. Manning
- 日期:2014
- 期刊:EMNLP
2. 文章概括
文章提出了一种新的单词表示的训练方法:Glove。该方法结合了基于统计方法和基于上下文窗口方法的优势,在多个下游任务上超越了当下SOTA方法的表现。
3 文章重点技术
3.1 两种常用的单词向量训练方法
现有的两类常用的单词向量训练方法为
- 基于矩阵分解的方法,如LSA会首先计算一个term-document矩阵,每一列表示每个文档中各个单词的出现频率,然后进行奇异值分解;HAL则会首先计算一个term-term共现矩阵。但此类方法会被频繁出现的the, and等单词影响,计算相似度的时候该类对语义影响很小的单词会占较大的比重。
- 基于上下文窗口的方法,如Word2Vec[1]。此类方法没有用到语料中的统计信息,可能无法捕捉到数据中的重复现象。
3.2 GloVe
为了解决上述两种方法存在的问题,文章提出了一种Global Vectors(GloVe)单词嵌入方法,可以直接捕获语料中的统计信息。
首先,我们计算单词共现矩阵 X X X,其中 X i j X_ij Xij表示单词 j j j出现在单词 i i i的上下文的次数。令 X i = ∑ k X i k X_i = \sum_k X_{ik} Xi=∑kXik表示任意单词出现在单词 i i i上下文的总次数,则 P i j = X i j X i P_{ij} = \frac {X_ij}{X_i} Pij=XiXij表示单词 j j j出现在单词 i i i的上下文的概率。
为了得到每个单词的嵌入 w i w_i wi,文章首先需要假设一种嵌入 w i , w j w_i, w_j wi,wj和共现矩阵之间的关系式。为此,文章给出一个示例:如下表所示,假设考虑单词i=“ice”,j=“steam”,则k="solid"时,由于"solid"和"ice"相关性更高,所以 P i k / P j k P_{ik}/P_{jk} Pik/Pjk应该大一点,下表中实验结果为8.9;如果k=“gas”,和"steam"的相关性更高,从而 P i k / P j k P_{ik}/P_{jk} Pik/Pjk应该小一点,下表中实验结果为 8.5 × 1 0 − 2 8.5 \times 10^{-2} 8.5×10−2;如果k="water"和二者均相关或k="fashion"和二者均不相关,则 P i k / P j k P_{ik}/P_{jk} Pik/Pjk应该接近1,如下表中的 1.36 1.36 1.36和 0.96 0.96 0.96。

为此,文章选择通过单词 i , j i,j i,j之间的概率比值来进行建模: F ( w i , w j , w ~ k ) = P i k P j k F(w_i, w_j, \tilde{w}_k) = \frac {P_{ik}}{P_{jk}} F(wi,wj,w~k)=PjkPik,其中 w i , w j , w ~ k w_i, w_j, \tilde{w}_k wi,wj,w~k分别表示 i , j , k i, j, k i,j,k的词向量, w ~ \tilde{w} w~也是待学习的参数,和 w w w本质上没有区别,只是通过不同的初始化得到的,用于区分探针单词( k k k)和共现单词,类似transformer中的Q,K含义。考虑到单词空间一般是线性的,我们用 w i − w j w_i - w_j wi−wj表示向量之间的差异: F ( w i − w j , w ~ k ) = P i k P j k F(w_i- w_j, \tilde{w}_k) = \frac {P_{ik}}{P_{jk}} F(wi−wj,w~k)=PjkPik,又因为上式左边的输入为两个向量,右边为标量,故我们考虑用向量的点积: F ( ( w i − w j ) T w ~ k ) = P i k P j k F((w_i -w_j)^T\tilde{w}_k) = \frac {P_{ik}}{P_{jk}} F((wi−wj)Tw~k)=PjkPik。由于单词的共现矩阵中,单词和上下文单词是任意指定的,我们可以自由交换当前单词和上下文单词,从而我们要保证交换 w ↔ w ~ w \leftrightarrow \tilde{w} w↔w~和 X ↔ X T X \leftrightarrow X^T X↔XT后上式仍然成立,故我们首先需要 F F F为一个同态映射: F ( ( w i − w j ) T w ~ k ) = F ( w i T w ~ k ) F ( w j T w ~ k ) F((w_i -w_j)^T\tilde{w}_k) = \frac {F(w_i^T\tilde{w}_k)}{F(w_j^T\tilde{w}_k)} F((wi−wj)Tw~k)=F(wjTw~k)F(wiTw~k),从而有 F ( w i T w ~ k ) = P i k = X i k X i F(w_i^T\tilde{w}_k) = P_{ik} = \frac {X_{ik}}{X_i} F(wiTw~k)=Pik=XiXik。由于上式的解为 F = exp F=\exp F=exp,从而 exp ( w i T w ~ k ) = P i k = X i k X i ⟹ w i T w ~ k = log P i k = log ( X i k X i ) = log ( X i k ) − log ( X i ) \exp (w_i^T \tilde{w}_k) = P_{ik} = \frac {X_{ik}}{X_i}\\\implies w_i^T \tilde{w}_k = \log P_{ik} = \log \left(\frac {X_{ik}}{X_i}\right) = \log(X_{ik}) - \log (X_i) exp(wiTw~k)=Pik=XiXik⟹wiTw~k=logPik=log(XiXik)=log(Xik)−log(Xi);其次考虑到上式的 log ( X i ) \log (X_i) log(Xi)与 k k k无关,故可以写作偏差 b i b_i bi,再增加 w ~ k \tilde{w}_k w~k的偏差 b ~ k \tilde{b}_k b~k,我们得到 w i T w ~ k + b i + b ~ k = log ( x i k ) w_i^T \tilde{w}_k + b_i + \tilde{b}_k = \log(x_{ik}) wiTw~k+bi+b~k=log(xik)满足上述对称要求。在此基础上增加权重函数 f ( X i j ) f(X_{ij}) f(Xij)可以保证共现太频繁的元素不会被过分的重视,且稀有的共现元素也不会被过分重视。这就要求 f f f满足非递减且有明确上界,如下函数满足条件: f ( x ) = { ( x / x m a x ) α i f x < x m a x , 1 , o t h e r w i s e f(x) = \begin{cases}(x/x_{max})^{\alpha} \quad &if \ x < x_{max},\\1, \quad &otherwise \end{cases} f(x)={(x/xmax)α1,if x<xmax,otherwise。函数曲线如下图所示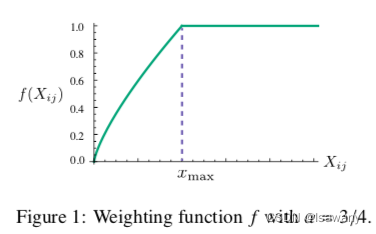
3.3 模型的复杂度
文章证明,当 α = 1.25 \alpha = 1.25 α=1.25时交过较好,此时模型的复杂度为 O ( ∣ C ∣ ) \mathcal{O}(|\mathcal{C}|) O(∣C∣),其中 C \mathcal{C} C表示语料库。相比于其他基于上下文窗口的方法复杂度 O ( V 2 ) \mathcal{O}(V^2) O(V2)更低。
4. 文章亮点
文章提出了基于将上下文窗口和共现矩阵结合的词向量嵌入方法GloVe,数值实验表明,GloVe在单词相似度、单词类比和NER等任务上相比于其他SOTA方法有明显提升。
5. 原文传送门
[GloVe: Global Vectors for Word Representation](GloVe: Global Vectors for Word Representation)
6. References
[1] 论文笔记–Efficient Estimation of Word Representations in Vector Space
)

 剑指 Offer 27. 二叉树的镜像 ——【Leetcode每日一题】)
基础)
)


)




)
)





