
市面上大部分的免费CRM不需要付费即可使用,但是对于使用人数和功能进行了部分限制。下面我们就来说说,免费CRM的适用对象是谁?
1、初创/小微企业
这种小微企业没有太多的资金,也没有复杂的客户管理需求,仅仅需要一款工具帮助企业进行管理。免费CRM的功能虽然做了限制,但是完全足够使用,可以帮助小微企业节省成本,建立客户数据库,提高工作效率。
2、非盈利组织
非盈利组织没有太多的收入来源,但是却有着管理志愿者和合作伙伴,建立良好关系的需求。免费CRM可以帮助他们录入和管理这些人的信息,做到井井有条,提高组织管理能力。
3、个人用户
对个人用户来说,免费CRM是更好的选择。他们通常没有固定的工作地点,但是需要与客户或合作方保持沟通和协作。免费CRM可以帮助他们随时随地地记录和查询客户信息,跟进项目进度,而且无需投入。
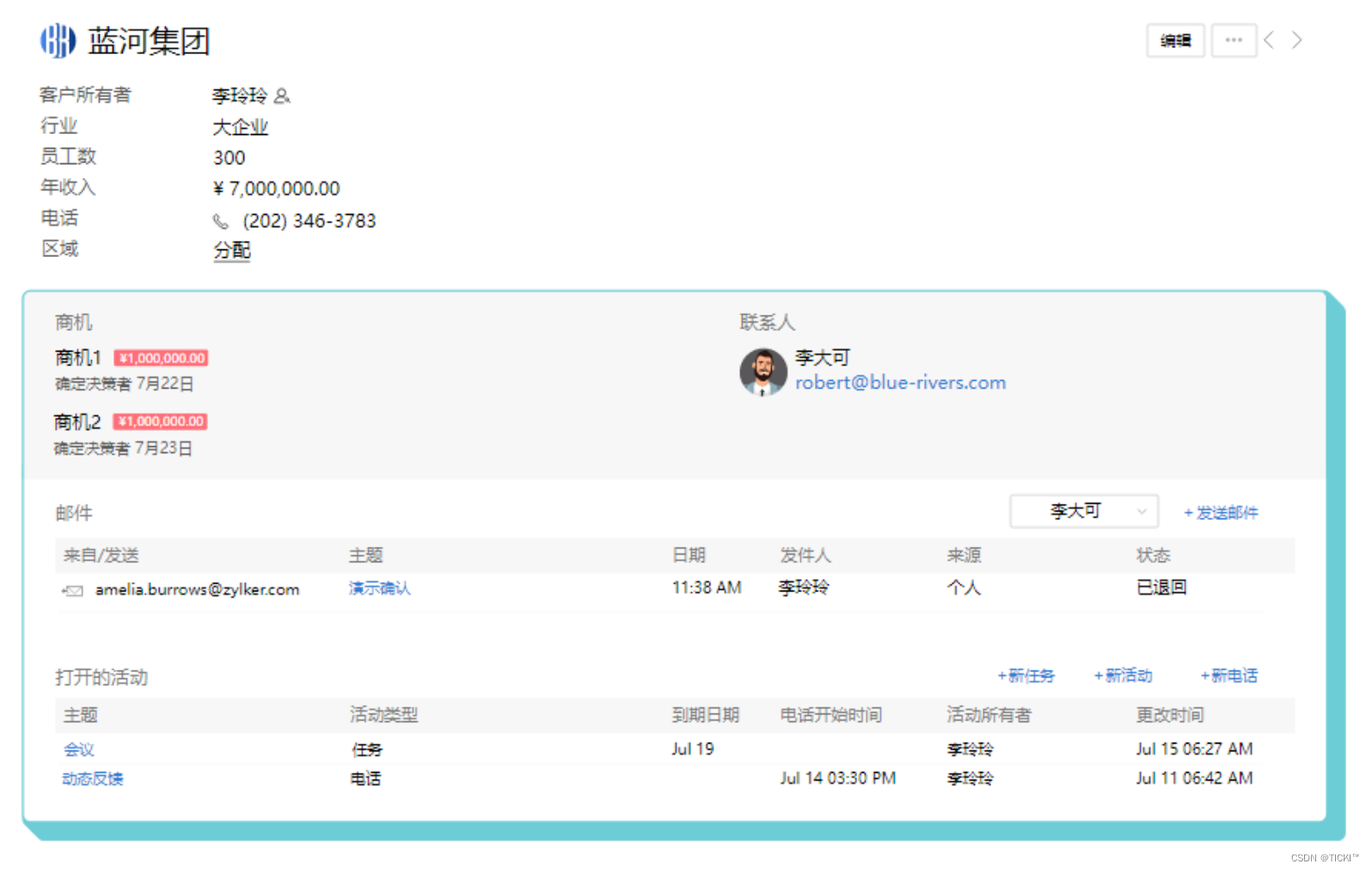
总结来说,免费CRM适用于那些没有现金流不充裕,没有复杂客户管理需求的小微企业、非盈利组织和个人用户。Zoho CRM免费版,3名用户及以下永久免费,仅仅限制了部分高级功能。后续业务规模扩大,还可以一键升级到付费版本,非常灵活。


)




)




)






)