1.问题的提出
1.1关系模式的表示
关系模式由五部分组成,是一个五元组:R(U,D,DOM,F)
| 元组 | 概念 |
|---|---|
| R | 关系名R是符号化的元组语义。 |
| U | U为一组属性。比如学号,姓名。 |
| D | D为属性组U中的属性所来自的域。比如年龄的取值范围。 |
| DOM | DOM为属性到域的映射。具体的取值。 |
| F | F为属性组U上的一组数据依赖。 |
【说明】
(1)由于D、DOM与模式设计关系不大,因此在本章中把关系模式看作一一个三元组: R<U、F>。R就相当于表的名字,U就是表中的每个字段属性,F就是每个字段之间的属性关系。
(2)当且仅当U上的一个关系r满足F时,r称为关系模式R<U,F>的一个关系。r就相当于实际的值之间的关系。
(3)作为二维表,关系要符合一个最基本的条件:每个分量必须是不可分开的数据项。满足了这个条件的关系模式了就属于第一范式(1NF)。每一行可能叫元组也有的叫记录。
1.2 数据依赖
数据依赖是一个关系内部属性与属性之间的一种约束关系是通过属性间值的相等与否体现出来的数据间相互联系。
数据依赖的主要类型:
- 函数依赖(Funct ional Dependency, 简记为FD)
- 多值依赖(Multi-Valued Dependency,简记为MVD)
1.3.函数依赖在现实生活中的体现
例1:
描述一个学生关系,可以有学号、姓名、系名等属性。一个学号只对应一个学生,一个学生只在一个系中学习,“学号”确定后,学生的姓名及所在系的值就被唯一确定。
Sname=f (Sno),
Sdept=f (Sno)即Sno函数决定Sname, Sn确定Sdept,
记作Sno->Sname, Sno-> Sdept.
例2:
建立一个描述学校教务的数据库。涉及的对象包括:学生的学号、(Sno) 、所在系(Sdept)、系主任姓名(Mname) 、课程号(Cno)、成绩(Grade)。。
假设学校教务的数据库模式用一个单一的关系模式Student来表示,则该关系模式的属性集合为:
U= {Sno, Sdept, Mname, Cno, Grade}
现实世界的已知事实(语义) :
- 一个系有若干学生,但-一个学生只属于一个系;
- 一个系只有一名(正职)负责人;
- 一个学生可以选修多门课程,每门课程有若干学生选修:
- 每个学生学习每一门课程有一一个成绩。
由此可得到属性组U.上的一-组函数依赖F:
F= {Sno->Sdept, Sdent -> Mname, (Sno,Cno)->Grade}
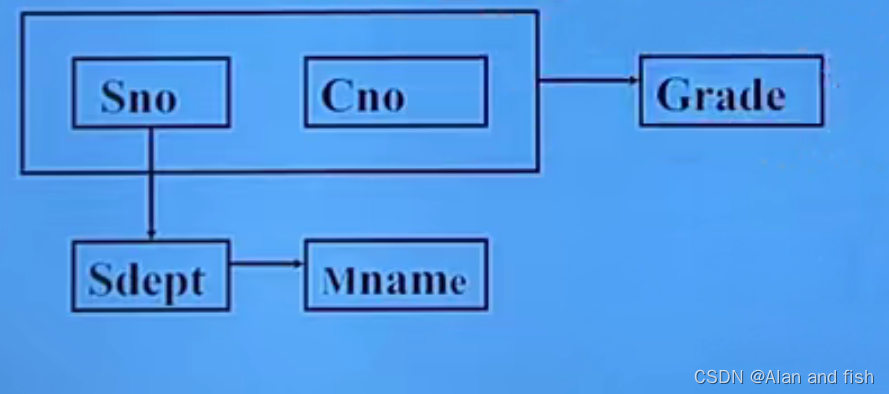
1.4 函数依赖中存在的问题
- 数据冗余
- 更新异常
- 插入异常
- 删除异常
为了解决这些问题就需要使用到规范
2.规范化
2.1 函数依赖
【定义1】设R (U)是属性集U上的关系模式,X、 Y是U的子集。若对于R (U)的任意一个可能的关系r,r中不可能存在两个元组上的属性值相等,而在Y上的属性值不等,则称“X函数确定Y”或“Y函数依赖于X”,记作X->Y。
函数依赖有以下5种:
| 依赖关系 | 概念 | 数学表示 |
|---|---|---|
| 非平凡函数依赖 | X → \rightarrow →Y,但Y ⊊ \subsetneq ⊊X | |
| 平凡函数依赖 | X → \rightarrow →Y,但Y ⊆ \subseteq ⊆X | |
| 决定因素 | X → \rightarrow →Y,则X称之为函数依赖的决定因素 | |
| 完全函数依赖 | X → \rightarrow →Y,并且对X集合中的任何真子集X’,都有X’ ↛ \nrightarrow ↛Y,即Y依赖于X中的所有属性。 | X → F Y X\overset{F}{\rightarrow}Y X→FY |
| 部分函数依赖 | X → \rightarrow →Y,但又不完全依赖X的属性 | X → P Y X\overset{P}{\rightarrow}Y X→PY |
| 传递函数依赖 | 在R(U)中,如果X → \rightarrow →Y(Y ⊊ \subsetneq ⊊X),Y ↛ \nrightarrow ↛X,Y → \rightarrow →Z,Z ⊊ \subsetneq ⊊Y,则称Z对X是传递依赖 | X → 传递 Y X\overset{传递}{\rightarrow}Y X→传递Y |
| 直接函数依赖 | 如果在传递函数依赖中的X ← → \leftarrow\rightarrow ←→Y,则X就是直接能推出Z,称之为直接函数依赖 |
【例】Student (Sno, Sname, Ssex, Sage, Sdept)。
假设不允许重名,则有:
Sno ->Ssex, Sno–>Sage, Sno->Sdept, Sno->Sname
Sname->Ssex, Sname->Sage, Sname ->Sdept。
但Ssex->Sage, Ssex ↛ \nrightarrow ↛ Sdept。
2.2 码
码是关系模式中的一个重要概念。在数据库中有以下几种码:
| 码 | 概念 |
|---|---|
| 候选码 | 设K为R<U, F>中的属性或属性组合,若 K → F F K\overset{F}{\rightarrow}F K→FF,则K为R的候选码 |
| 超码 | 设K为R<U, F>中的属性或属性组合,,如果U部分函数依赖于K,即K-U,则K称为超码( Surpkey)。 候选码是最小的超码,即K的任意一个真子集都不是候选码。 |
| 主码 | 若候选码多于一个, 则选定其中的一个为主码(primary key)。 |
| 主属性 | 包含在任何一个候选码中的属性称为主属性(primeattribute) |
| 非主属性\非码属性 | 不包含任何候选码中的属性称为非主属性(nonprime attribute)或非码属性(non-key attribute)。 |
| 全码 | 整个属性都是码,则称为全码 |
2.3 第一范式(1FN)
【定义】数据表中的每一个属性都不可再分,就属于第一范式。比如说价格可以分为售价和进价,就不能直接用价格来表示,必须单独把他们进行表示。
2.4 第二范式(2FN)
【定义】若关系模式R∈1NF,并且每一个非主属性都完全函数依赖于任何一个候选码,则R∈2NF。
【例子】S-L-C(Sno, Sdept, Sloc, Cno, Grade), Sloc为学生的住处,并且每个系的学生住在同一个地方。S-L-C的码为(Sno, Cno)。
函数依赖有:
(Sno, Cno) → F \overset{F}{\rightarrow} →F Grade
Sno→Sdept, (Sno, Cno) → F \overset{F}{\rightarrow} →FSdept
Sno → \rightarrow →Sloc, (Sno, Cno) → P \overset{P}{\rightarrow} →PSIoc
Sdept → \rightarrow →Sloc
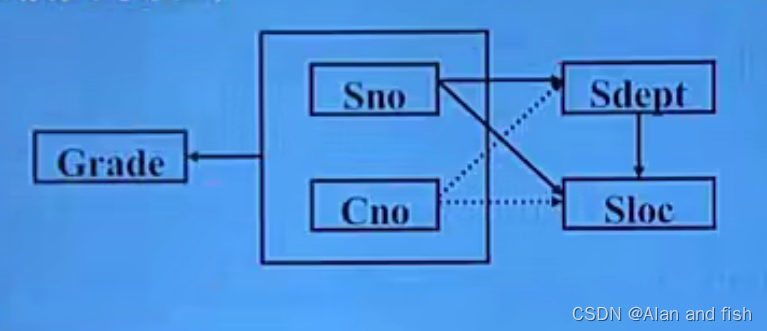
【说明】
①图中虚线表示部分函数依赖。
②非主属性Sdept、Sloc并不完全依赖于码。
③关系模式S-L-C不属于2NF。
因为在候选依赖中,非主属性(Sdep)部分依赖于候选码(Cno),所以不满足第二范式。
不满足2FN的会产生插入异常、删除异常、修改复杂等问题。
出现这种问题的原因:
例子中有两类非主属性: -类如Grade,它对码完全函数依赖,另一类如Sdept、Sloc, 它们对码不是完全函数依赖。
解决方法:
用投影分解把关系模式S-L-C分解成两个关系模式。
SC (Sno, Cno, Grade)。
S-L (Sno, Sdept, Sloc)。
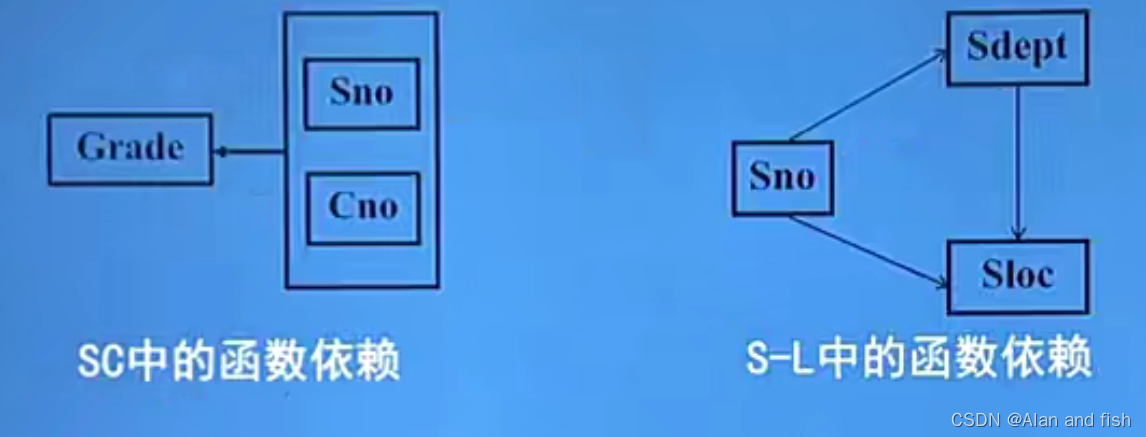
SC的码为(Sno, Cno),SL的码为Sno,这样使得非主属性对码都是完全函数依赖了。
2.5 第三范式(3FN)
[定义7]设关系模式R<U, F>∈1NF,若R中不存在这样的码X、属性组Y及非主属性Z (ZPY),使得X-→Y,Y→Z成立,Y → \rightarrow →X不成立,则称R<U, F>∈3NF。即第三范式中不能有传递依赖。
[例] SC没有传递依赖,因此SC∈3NF。
S-L中Sno → \rightarrow →Sdept (Sdept ↛ \nrightarrow ↛Sno),Sdept → \rightarrow →Sloc,
传递
可得Sno → 传递 \overset{传递}{\rightarrow} →传递 Sloc.
解决的办法是将S-L分解成:
S-D (Sno, Sdept) ∈ 3NF。
D-L (Sdept, Sloc) ∈3NF。
2.6 BC范式(BCNF)
BCNF (Boyce Codd Normal Form) 由Boyce和Codd提出, 比3NF更进了一步。通常认为BCNF是修正的第三范式,有时也称为扩充的第三范式。
【定义8】设关系模式R<U, F>∈1NF,若X→Y且Y ⊄ \not\subset ⊂X时X必含有码,则R<U, F> 属于BCNF。换言之,在关系模式R<U, F>中,如果每一个决定属性集都包含候选码,则R∈BCNF。
BCNF的关系模式所具有的性质:
(1)所有非主属性都完全函数依赖于每个候选码。比如能X → \rightarrow →Y,Y必须完全依赖于X中任何一个属性。
(2)所有主属性都完全函数依赖于每个不包含它的候选码。
(3)没有任何属性完全函数依赖于非码的任一组属性。
如果一个关系数据库中的所有关系模式都属于BCNF,那么数依赖范畴内,它已实现了模式的彻底分解,达到了最高的规程度,消除了插入异常和删除异常。
【例1】考察关系模式C (Cno, Cname, Pcno),它只有一个码Cno,没有任何属性对Cno部分依赖或传递依赖,F所以C∈3NF。同时中Cno是唯一的决定因素 ,所以C∈BCNF。Cno是课程编号,Cname是课程名字,Pcno是课程先导课。
由题知Cno → \rightarrow →Cname,Cno → \rightarrow →Pcno。
【例2】关系模式S (Sno, Sname, Sdept, Sage),假定Sname也具有唯一性,那么S就有两个码,这两个码都由单个属性组成,彼此不相交。其他属性不存在对码的传递依赖与部分依赖,所以S∈3NF。同时S中除Sno, Sname外没有其他决定因素,所以S也属于BCNF。
由题知:
Sno → \rightarrow →Sname
Sname → \rightarrow →Sno
则Sno ← → \leftarrow\rightarrow ←→Sname
Sno → \rightarrow →Sdept
Sno → \rightarrow →Sage
小结:
| 范式 | 简单概念 |
|---|---|
| 1FN | 属性不可再分 |
| 2FN | 不存在部分依赖 |
| 3FN | 不存在传递依赖 |
| BCFN | 在满足三大范式的条件下,没有属性依赖于非码属性 |



















)