第二章 计算机是如何学会下棋的
人类棋手在下棋时,会根据自己的经验只考虑在当前棋局下最重要的几个可能的走法,但是计算机没有这种经验。
知识太复杂了,需要考虑很多具体的情况,一旦知识总结的不到位,可能就会出现大的差错,总结知识让计算机使用应该是走不通的。
三、 α \alpha α- β \beta β 剪枝算法
1. 极小-极大模型存在的问题
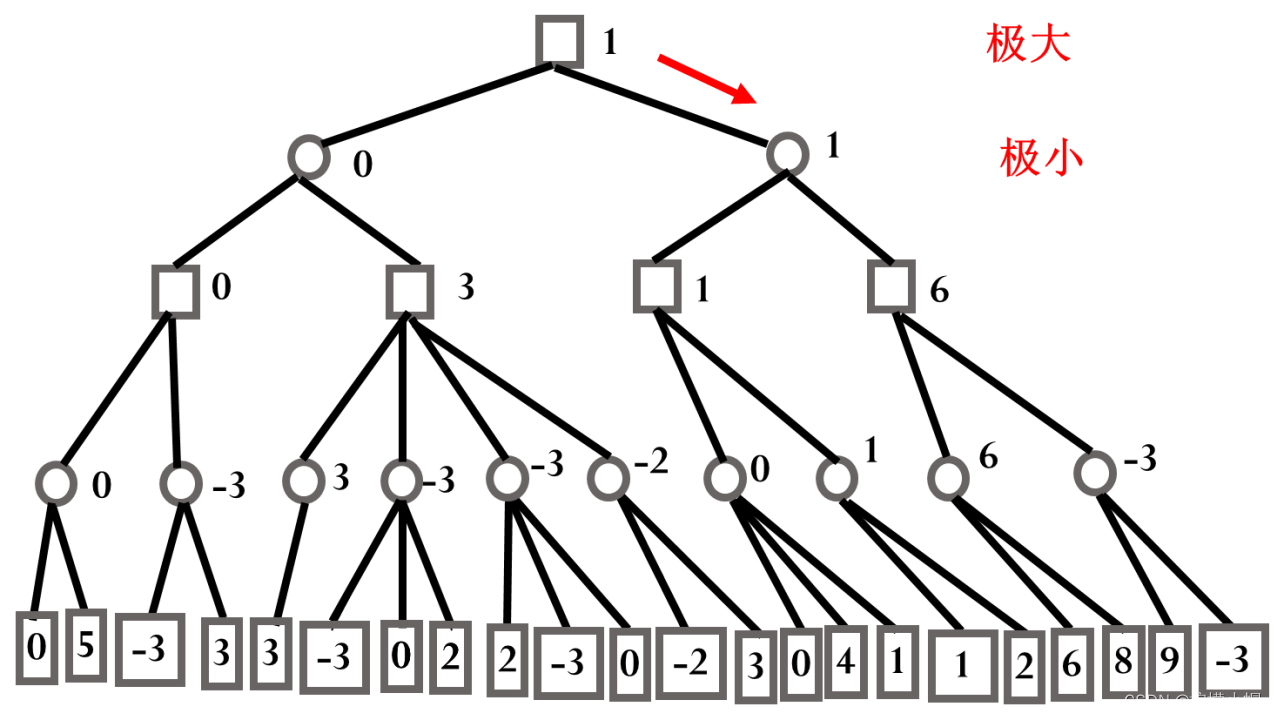
2. 人如何处理这个问题呢?

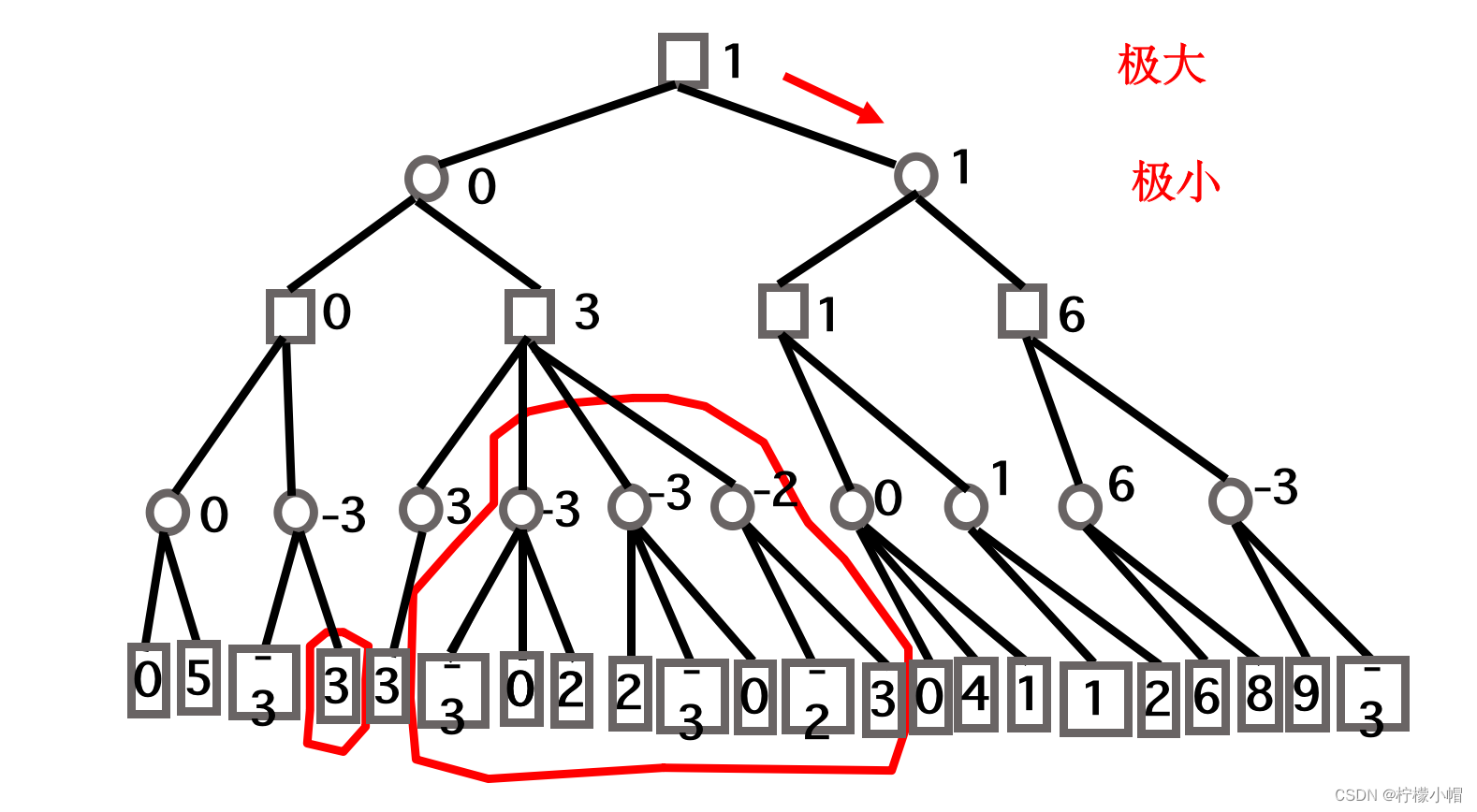
3. α \alpha α- β \beta β 剪枝算法
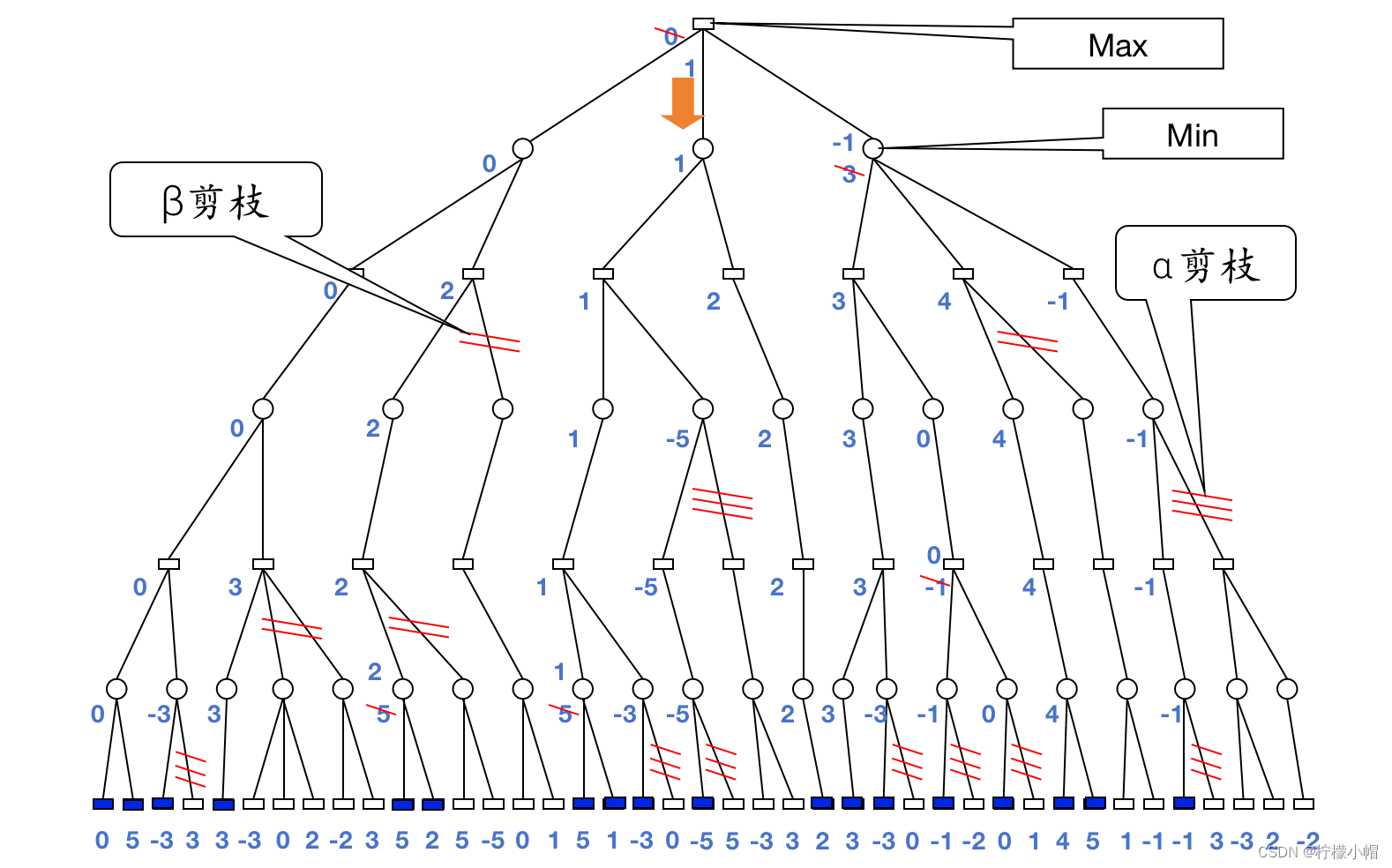
- 假设并不是一开始就将整个搜索图生成出来,而是按照一定的原则一点一点地产生。比如下图是一个搜索图,我们假设一开始并没有这个图,而是按照从上到下从左到右的优先顺序来生成这个图。我们先从最上边一个节点开始,按顺序产生 a、c、g、r 四个节点,假设就考虑 4 步棋,这时就不再向下生成节点了。由于 r 的分值为 0,而 g 是极小节点,所以我们知道 g 的分值应该 ≤0。接下来再生成 s 节点,由于 s 的分值为 5,g 是极小节点且没有其他子节点了,所以 g 的分值等于 0。由于 c 是极大节点,根据 g 的分值为 0,我们有 c 的分值 ≥0。再看 c 的其他后辈节点情况,生成 h 和 t 两个节点,由于 t 的分值为-3,而 h 是极小节点,所以有 h 的分值 ≤-3。
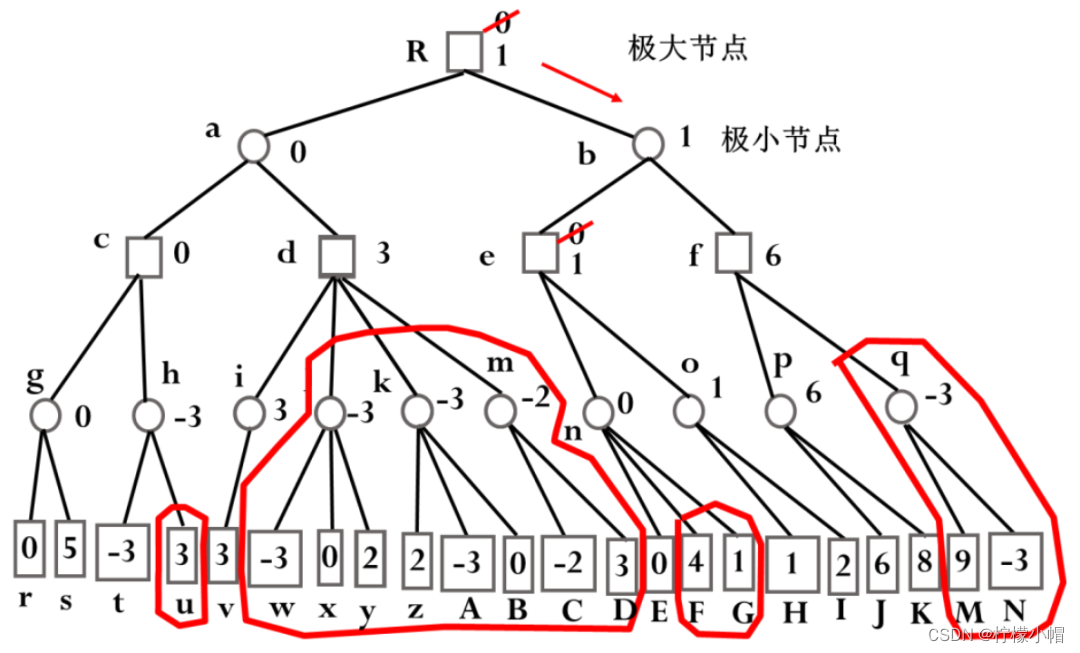
- c 的分值 ≥0,而 h 的分值 ≤-3,这时 u 的分值是多少都无关紧要了。
- 图中 u 的分值如果大于 h 的当前分值-3,则不影响 h 的分值,即便 u 的分值小于-3,比如-5,虽然改变了 h 的分值为 ≤-5,但是由于 c 是极大节点,c 的当前分值已经至少为 0 了,所以 h 的分值变小也不会改变 c 的分值。
- 这样的话,遇到图中这种 h 的当前分值小于 c 的当前分值这种情况时,由于 u 的分值是多少都不会影响 c 的分值了,所以就没有必要生成 u 这个节点了。这种情况我们称之为剪枝,其剪枝条件是如果一个后辈的极小节点(如图中的 h),其当前的分值小于等于其祖先极大节点的分值时(如图中的 c),则该后辈节点的其余子节点(如图中的 u)就没有必要生成了,可以被剪掉。注意这里用的是后辈节点和祖先节点,这是一种推广,因为这种剪枝并不局限于父节点和子节点的关系。
- 在确认了 c 的分值为 0 之后,同样的理由,我们可以确认 a 的分值 ≤0。生成 a 的后辈节点 d、i、v,由于 v 的分值为 3,且 d 向下就一条路,所以有 d 的分值 ≥3。由于 a 的分值最大为 0,而 d 的分值最小为 3,所以大的红圈圈起来的那些分支的分值是多少又没有意义了,a 取 c 和 d 中分值最小的,最终 a 取值为 0,大红圈圈起来的部分都没有必要生成了,又可以被剪掉。这里我们又发现了另外一个剪枝条件:如果一个后辈的极大节点的分值(如图中节点 d)大于等于其祖先极小节点的分值时(如图中节点 a),则该后辈节点还没有被生成的节点可以被剪掉,如图中大红圈圈起来的那些节点。
- a 的分值被确定为 0 之后,就可以确定 R 的分值 ≥0,继续向下生成节点 b、e、n、E,由于 E 的分值为 0,所以有 n 的分值 ≤0。n 是极小节点,其极大节点祖先有 e 和 R,e 这时还没有值,但是 R 的分值 ≥0,所以满足后辈极小节点的分值小于等于其祖先极大节点分值的剪枝条件,n 的两个子节点 F 和 G 都没有生成的必要,又可以被剪掉了。
- n 的分值被确定为 0,从而有 e 的分值 ≥0。接着生成节点 o 和 H,由于 H 的分值为 1,有 o 的分值 ≤1,不满足剪枝条件,生成节点 I,I 的分值为 2,o 是极小节点,所以 o 的分值确定为 1。e 是极大节点,从 n 和 o 的分值中选取最大的,从而更新 e 的取值,由原来的 0 修改为 1。e 的分值确定为 1 后,有 b 的分值 ≤1。继续生成 b 的后辈节点 f、P、J,J 的分值为 6,得到 P 的分值 ≤6,不满足剪枝条件,继续生成子节点 K,得到 K 的分值为 8,P 是极小节点,选取子节点中最小的值 6,从而确定 f 的分值 ≥6。后辈极大节点 f 的分值 6 大于等于其前辈极小节点 b 的分值 1,满足剪枝条件,q、M、N 三个节点被剪枝,从而确定 b 的分值为 1。R 的分值取 a、b 中最大者,从而用从节点 b 得到的 1 代替原来从 a 得到的 0。搜索过程到此结束,按照刚才的搜索结果,甲方应该选择 b 作为行棋的最佳走步,如图中的红色箭头所示。
- 这种方法就是 α-β 剪枝算法,可以利用已有的搜索结果,剪掉一些不必要的分枝,有效提高了搜索效率。

- 深蓝就是用了 α-β 剪枝算法,从而可以在规定的时间内完成一次行棋过程。
- 这种 α-β 剪枝算法得到的最佳走步跟极小-极大模型得到的结果是一样的。α-β 剪枝只是剪掉了那些不改变结果的分枝,所以不影响最终选择的走步。
- 那些分值是如何得到的?何处发生剪枝完全取决于那些分值,如果分值不准确则得到的结果也就值得怀疑了。
4. 如何估值?

- 这些分值是非常重要的。据深蓝的研发者介绍说,他们聘请了好几位国际象棋大师帮助他们整理知识,用于估算分值。但是基本思想并不复杂,大概就是根据甲乙双方剩余棋子进行加权求和,比如一个皇后算 10 分,一个车算 7 分,一个马算 4 分等。然后还要考虑棋子是否具有保护,比如两个相互保护的马,分数会更高一些,其他棋子也是大体如此。然后再考虑各种残局等,按照残局的结果进行估分。当然,这里给出的各个棋子的分数只是大概而已。最后甲方得分减去乙方得分就是该棋局的分值。
- 这个估值虽然看起来有些粗糙,但是由于在剪枝过程中探索的比较深,对于象棋来说,无论是国际象棋还是中国象棋,在探索的比较深的情况下,凭借棋子的多少基本就可以评判局面的优劣了,所以可以得到比较准确的估值。
- 所以对于计算机下棋来说,探索的越深其棋力也就越强,在可能的情况下,应该尽可能探索的更深一些。
5. α \alpha α- β \beta β 剪枝效果如何?

6. 几点注意

α-β 剪枝的关键点
-
在判断是否剪枝时,都是后辈极小节点与祖先极大节点进行比较、后辈极大节点与祖先极小节点做比较。当后辈极小节点的值小于等于祖先极大节点的值时,发生剪枝;当后辈极大节点的值大于等于前辈极小节点的值时,发生剪枝。
-
在判断是否剪枝时,一定要注意不只是与父节点做比较,还要考虑祖先节点。
-
在完成一次 α-β 剪枝后,只是选择了一次行棋,下一次应该走什么棋,应该在对方走完一步棋后,根据棋局变化进行 α-β 剪枝过程,再次根据搜索结果确定走什么棋。
7. 总结

-
对于真实的棋类游戏,由于其状态数过于庞大,不可能通过穷举所有状态的方法获得最佳走步。受人类下棋时思考过程的启发,提出了计算机下棋的极小-极大模型。该模型只在有限步内搜索,获得有限范围内的最佳走步。但同样由于棋类变化太多,即便是有限范围的搜索也是非常花费时间的。人类棋手在做极小-极大搜索的时候,并不是考虑有限范围内的每一种可能的走法,而是根据经验砍掉大量的不合理分枝,从而极大地缩小了搜索范围。受此启发提出了 α-β 剪枝算法,与人类利用经验砍掉大量不合理分枝不同,计算机并没有这种经验,而是利用已有的搜索结果,砍掉没有必要产生的分枝,有效地提高了搜索效率。深蓝就是采用的这种方法。
-
α-β 剪枝条件:
-
当后辈的极小节点值小于等于其祖先的极大节点值时,发生剪枝。
-
当后辈的极大节点值大于等于其祖先的极小节点值时,发生剪枝。
-
-
注意:比较时不只是与其父节点做比较,还要与其祖先节点做比较,只要有一个祖先节点满足比较的条件,就发生剪枝。
-
α-β 剪枝算法所得到的最佳走步质量严重依赖于最底层节点估值的准确性,搜索的越深,估值越准确。这是因为越深的节点其对应的棋局中棋子越少,而棋子比较少的情况下,其局面的估值也就会比较准确。这与人下棋时的思考也是一致的。
-
α-β 剪枝算法结束时得到的只是当前棋局下的一步走法,相当于我们思考了半天决定了一步棋如何走,后面如何进行,需要待对方走完一步棋后再次进行 α-β 剪枝搜索获得下一步棋的走法。也就是说,每行棋一次都需要进行一次 α-β 剪枝搜索。