算法-简单-二叉树-翻转、对称

记录一下算法题的学习8

翻转二叉树

翻转二叉树题目

给你一棵二叉树的根节点 root ，翻转这棵二叉树，并返回其根节点。

举例：给定root[5,3,7,2,4,6,10] 翻转成为root[5,7,3,10,6,4,2]

即所有的根节点的左右节点都要互换位置，输出的左右子树的位置跟输入正好是相反的

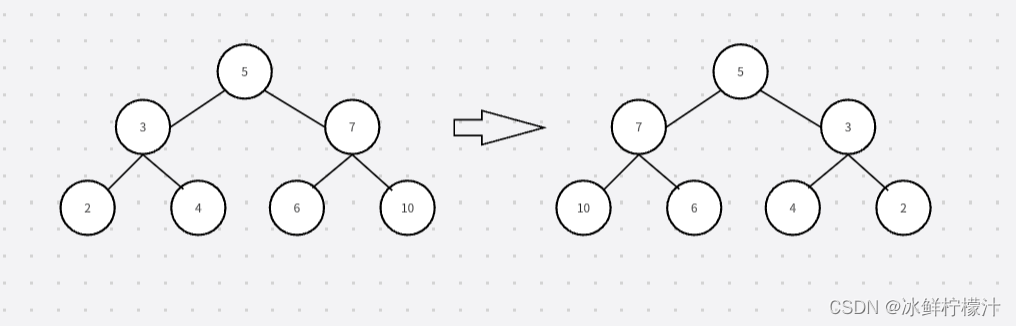
在经历前面一些简单二叉树的学习，递归的方法很快就做出来了

递归-深度优先搜索

class Solution {public TreeNode invertTree(TreeNode root) {if(root == null){return  null;}TreeNode left=invertTree(root.left);TreeNode right=invertTree(root.right);//这里就是进行二叉树的翻转root.left=right;root.right=left;//错误写法// right=root.left;// left=root.right;return root;}
}

迭代-广度优先搜索-层层扫荡代码展示：

class Solution {public TreeNode invertTree(TreeNode root) {if(root == null){return  root;}//将二叉树中的节点逐层放入队列中，再迭代处理队列中的元素Queue<TreeNode> queue = new LinkedList<TreeNode>();queue.add(root);//由此循环处理每一个节点while(!queue.isEmpty()) {//每次都从队列中拿一个节点，并交换这个节点的左右子树//了解public E poll () 返回值： 该方法从此队列的开头返回元素；如果此队列为空，则返回null。TreeNode temp = queue.poll(); //这里第一次出来的就是根节点TreeNode  deposit  = temp.left;//我们将根节点的的第一个左子节点暂时存放在存放点deposit中temp.left = temp.right;//这里就能进行交换-->使根节点的的第一个右子节点占据原本根节点的的第一个左子节点的位置temp.right =deposit;//而原本根节点的的第一个右子节点的值就变成了根节点的的第一个左子节点//接下来就是重复逐层操作//如果当前节点的左子树不为空，则放入队列等待后续处理if(temp.left!=null) {queue.add(temp.left);}//如果当前节点的右子树不为空，则放入队列等待后续处理if(temp.right!=null) {queue.add(temp.right);}}//返回处理完的根节点return root;}
}

对称二叉树

二叉树题目

给你一个二叉树的根节点 root ，检查它是否轴对称。

什么是轴对称？

如果一个图形沿一条直线折叠，直线两旁的部分能够完全重合，那么直线两旁的部分成轴对称

举例root[1,2,2,3,4,4,3]

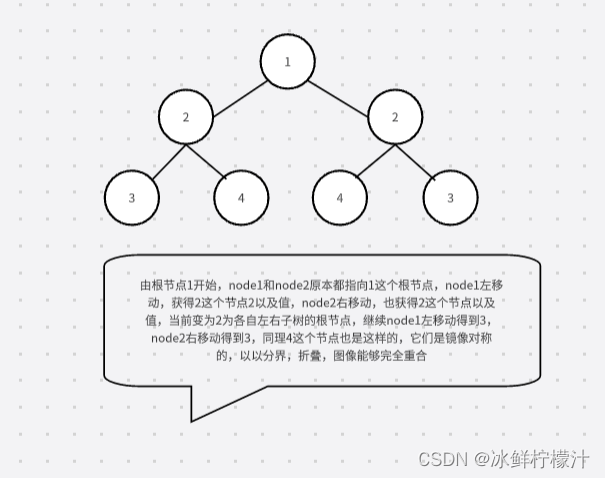
而root[1,2,2,null,3,null,3]

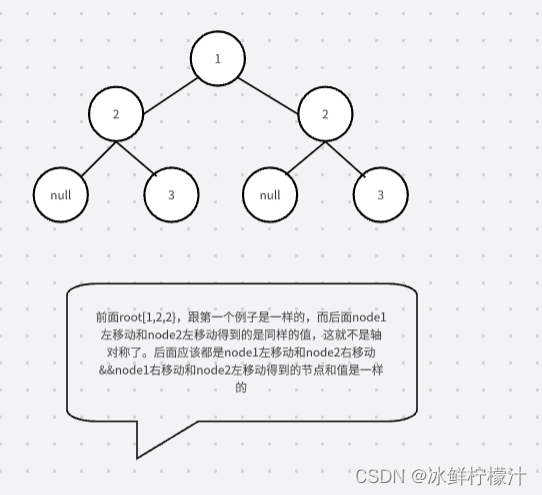
代码实现

*通过「同步移动」两个指针的方法来遍历这棵树，node1 指针和 node2 指针一开始都指向这棵树的根，随后 node1右移时，node2左移，node1左移时，node2右移。每次检查当前 node1 和 node2节点的值是否相等，如果相等再判断左右子树是否对称。*/
class Solution {public boolean isSymmetric(TreeNode root) {return check(root,root);}public boolean check(TreeNode node1,TreeNode node2){if(node1==null&&node2==null){return true;}if(node1==null||node2==null){return false;}return node1.val==node2.val && check(node1.left,node2.right) && check(node1.right,node2.left);}
}