系列文章目录

什么是计算机网络？
什么是网络协议？
计算机网络的结构
数据交换之电路交换
数据交换之报文交换和分组交换
分组交换 vs 电路交换
计算机网络性能（1）——速率、带宽、延迟
计算机网络性能（2）——时延带宽积、丢包率、吞吐量/率
计算机网络体系结构概念
OSI参考模型基本概念
OSI参考模型中非端-端层（物理层、数据链路层、网络层）功能介绍
OSI参考模型中端-端层（传输层、会话层、表示层、应用层）功能介绍
TCP/IP参考模型基本概念，包括五层参考模型
网络应用的体系结构
网络应用进程通信
网络应用对传输服务的需求
Web应用之HTTP协议（涉及HTTP连接类型和HTTP消息格式）
Cookie技术
Web缓存/代理服务器技术
传输层服务概述、传输层 vs. 网络层
传输层——多路复用和多路分用
传输层——UDP简介
传输层——可靠数据传输原理之Rdt协议
传输层——可靠数据传输之流水线机制与滑动窗口协议
传输层——TCP特点与段结构
传输层——TCP的可靠数据传输
TCP连接管理（图解三次握手和四次挥手）
传输层——拥塞控制原理与解决方法
TCP的拥塞控制机制
网络层服务与核心功能
网络层服务模型——虚电路网络
网络层服务模型——数据报网络
Internet网络的网络层——IP协议之IP数据报的结构
IP分片
IP编址与有类IP地址
IP子网划分与子网掩码
CIDR与路由聚合
DHCP协议
网络地址转换(NAT)
ICMP（互联网控制报文协议）
IPv6简介

---

---

网络抽象

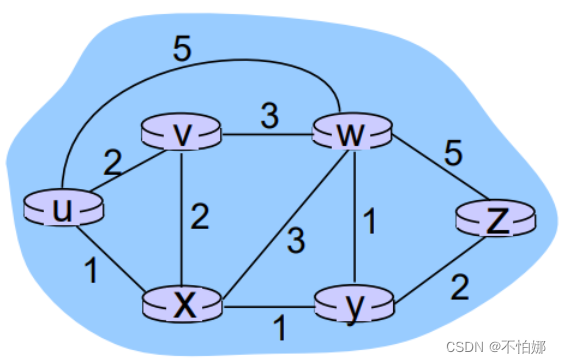
我们可以将网络抽象为一个图。图是由一些结点和边构成的拓扑结构。图的抽象在网络领域应用很广泛。

• 图: G = (N, E)

• 网络中的路由器会被抽象为图中的结点。N = 路由器集合= { u, v, w, x, y, z }

• 路由器之间的链路抽象为图中的边。E = 链路集合 ={ (u,v), (u,x), (v,x), (v,w), (x,w), (x,y), (w,y), (w,z), (y,z) }

• 权值代表网络中链路的费用或者说距离、代价。描述了这个链路的成本大小。比如图中的c(w, z) = 5

我们在描述一个路径的费用的时候，就是从源到目的经过的每段链路的费用之和。一般原则是费用越小，路径越好。所以在路由的过程中，关键问题就是源到目的（如u到z）的最小费用路径是什么。为了解决这样的问题，需要网络中每个路由器运行路由算法即寻找最小费用路径的算法。

路由算法分类

对于不同的分类标准，分类是不一样的。

• 静态路由 vs 动态路由？
  • 静态路由：即手工配置的路由。这种路由更新慢，但是优先级高
  • 动态路由：基于某些路由算法动态地计算而来。这种路由更新快，可以实现定期更新。优点在于能够及时响应链路费用或网络拓扑变化
• 全局信息 vs 分散信息？
  • 全局信息：路由算法或路由协议进行计算的时候需要掌握完整的网络拓扑和链路费用信息。换句话说掌握那张抽象的图。最具代表性也是被广泛使用的是链路状态(LS)路由算法
  • 分散(decentralized)信息：路由器只掌握物理相连的邻居以及链路费用，在这个基础上通过邻居间信息交换和多次的迭代计算以后，就可以找到到达目的网络最佳的路由信息。比如距离向量(DV)路由算法

链路状态路由算法

说明

链路状态路由算法基于Dijkstra（迪杰斯特拉） 算法来设计。

首先需要考虑的问题就是结点如何掌握整张图和链路费用。那就要求每个路由器构造一个链路状态分组然后广播出去，这个分组包括这个路由器与之相连的所有邻居路由器的ID，以及与这些路由器直接相连的链路的费用。这样任何一个路由器最后都会集齐网络中所有结点广播的链路状态分组，然后路由器就可以基于这些信息构造网络完整的拓扑和费用信息。这样每一个路由器就可以基于它所构造的网络这张图去求最短路径了。

通过Dijkstra 算法，k次迭代后，就能得到到达k个目的结点的最短路径

这里给出Dijkstra 算法需要用到的一些符号及其含义：

• c(x,y) : 结点x到结点y链路费用；如果x和y不直接相 连，则为∞
• D(v) : 从源即计算结点到目的v的当前路径费用值。注意不一定是最短的
• p(v) : 沿从源到v的当前路径，v的前序结点
• N’ : 已经找到最小费用路径的结点集合

下面来看一下这个算法的伪代码：

示例

通过一个例子看一下这个过程：

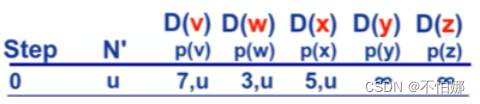
• 初始化，从u结点开始。v、w、x都与u相邻，所以它们的D值和p都能够准确确定。而y、z与u不相邻，记为∞

  

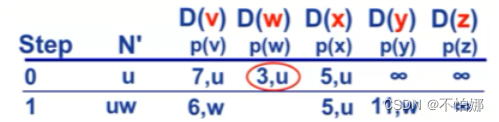
• 进入循环。目前除了u以外的结点都不在N‘ 中，并且D(w)是最小的，所以将w加入N‘ 中。然后更新w的所有邻居。可以看到，到达v的路径费用原先是7，如果通过w到达v就是6，以此类推更新与w相邻的结点路径的费用

  

• 以此类推，经过5次迭代就找到了从u到其他结点的最短路径。这里u到v的最短路径大小是6，到w是3，到x是5……

  

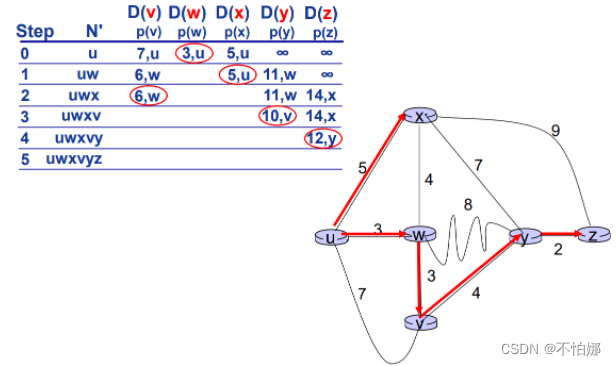
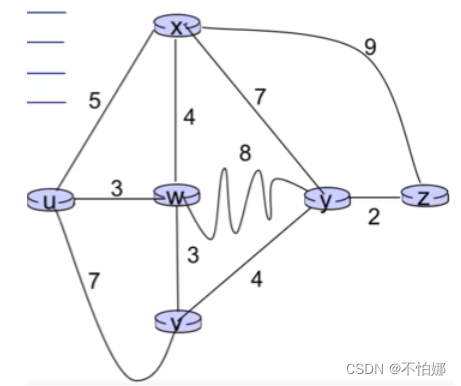
下面再看一个例子：

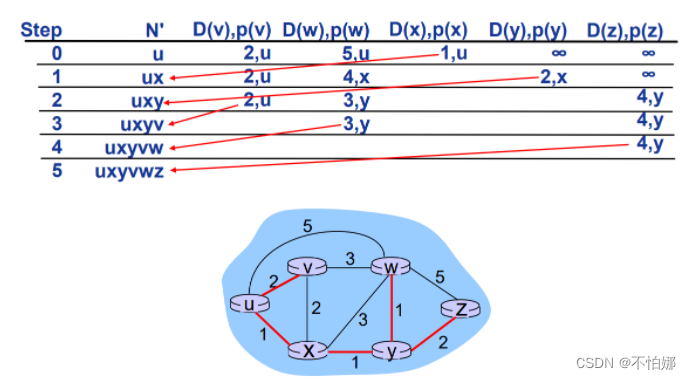
大家可以自行计算一下。最终u就可以获得一个最短路径树：

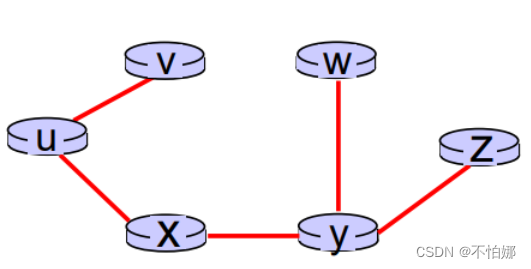
然后将这个树反映在转发表中。比如这个例子中，如果要把数据送到v，就从(u,v)这条链路发送，而发向x、y、w、z的数据都要从(u,x)这条链路发送。

但是使用链路状态路由算法可能会产生震荡(oscillations)现象。因此使用这种算法的路由协议往往会采用一些机制去避免这种现象的发生。