前 言
大语言模型,尤其是基于思维链提示词(Chain-of Thought Prompting)[1]的方法,在多种自然语言推理任务上取得了出色的表现,但不擅长解决比示例问题更难的推理问题上。本文首先介绍复杂推理的两个分解提示词方法,再进一步介绍将提示词方法应用于知识图谱复杂逻辑推理的工作。

文章一:“Least-to-Most Prompting”[2]
让大模型学会处理更复杂的推理
本文首先提出了Least-to-Most Prompting方法的动机,是人类智慧与机器学习之间的三个差异:
(1)面对一个新问题时,人类可以通过很少的示例中解决它,但机器通常需要大规模的标注语料;
(2)人类可以很清楚的阐释所做预测的隐含原因,但机器学习是一个黑盒子;
(3)人类可以解决比之前见过的问题更难的问题,但机器学习只能解决与之前相同难度的问题。
Google Brain在2022年提出Chain-of-Thought方法,利用few-shot prompting尝试填补人类智慧和机器学习之间的差距,但他不能解决比实例问题更难的问题。为此,该团队提出了Least-to-Most Prompting方法,该方法分为两个阶段:第一阶段将一个复杂问题分解为一个简单子问题序列;第二阶段按顺序解决子问题,且回答后续子问题会依赖前序子问题的答案。
下图给出了Least-to-Most Prompting方法解决一个数学问题的示例:
(1)将复杂问题分解为简单子问题;
(2)按序解决子问题,其中,回答第二个子问题时使用了第一个子问题的答案。
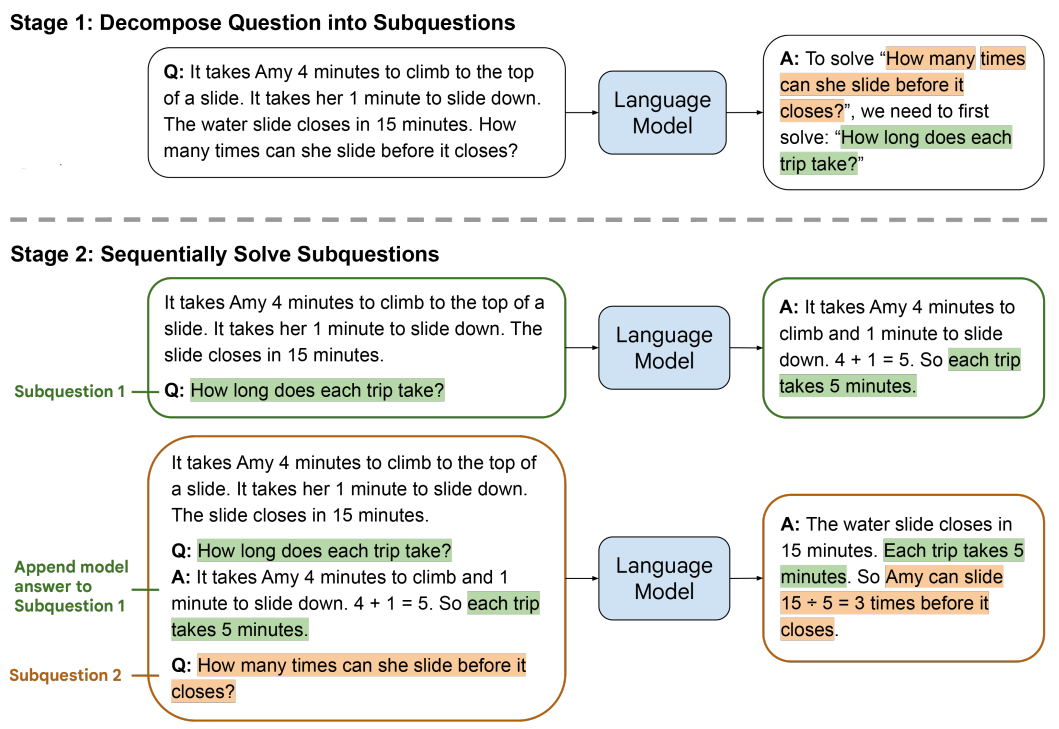
实验部分,论文通过符号操作(symbolic manipulation)、组合泛化(compositional generalization)和数学推理(math reasoning)三类任务来验证Least-to-Most Prompting的效果,并与Chain-of-Thought Prompting方法进行比较。
符号操作任务的输入是一个单词列表,对应输出是将这个单词列表中所有单词最后一个字母连接起来。如,“thinking machine”的输出为“ge”。
如图,Least-to-Most Prompting方法首先将一个长的单词序列转化为子序列,

再逐步解决每个子序列最后一个字母的连接问题,并且在解决更复杂的问题时,会根据前序简单问题的答案(如已知“think, machine” outputs “ke”)得到后序问题的结果。

Chain-of-Thought Prompting则与此不同,如下图,该方法不会顺序的解决子问题,而是每一次都将符号操作的问题作为一个独立的新问题给出具有推理过程的提示词示例。

在连接最后一个字母这类符号操作的任务中,随着不同单词量L的变化,Least-to-Most Prompting方法的准确率都远好于其他提示词方法,尤其是当单词量变大时,Chain-of-Thought方法准确率下降速度远大于Least-to-Most方法,这也说明Least-to-Most方法处理比示例更难的问题时更具有优势。

组合泛化任务是给出一个指令,将其翻译为一个动作序列。

下图给出了Least-to-Most Prompting方法第一步将复杂指令分解为简单指令的提示词示例,

和第二步解决每个简单指令给出的提示词序列。

在SCAN数据集上,Least-to-Most Prompting方法的准确率都远优于其他提示词方法,该方法仅需要少数的提示词示例,就可以解决同等或更难的推理问题,具有较好的泛化能力。

在数学推理任务中,Least-to-Most Prompting也是先通过分解问题,将下图中的复杂问题分解为两个简单子问题,再依次解决这个两个子问题得到最终的答案。

在DROP和GSM8K数据集上,Least-to-Most Prompting的方法都具有较高的准确率,尤其是DROP数据集上效果提升更加明显。


文章二:”Successive Prompting”[3]
连续提示词解决复杂任务
Successive Prompting工作与Least-to-Most Prompting是同时期的工作,他们的核心思想类似,都是将复杂的问题先分解为简单的问题再分别解决。但Successive Prompting方法并不是在一开始就将复杂问题分解为多个子问题,而是每一次都分解出下一个要解决的子问题,让大语言模型去回答该子问题。再将复杂问题和上一个问题的答案一起输入,去分解下一个要解决的子问题,并进行回答。一直重复上述过程,直到大模型给出没有问题需要回答,最后一个子问题的答案就是复杂问题的答案。
Successive Prompting方法可以看做是一个迭代的提示词方法,下图给出了该方法每一个迭代过程,以及没有其他问题后得到最终的过程示例。
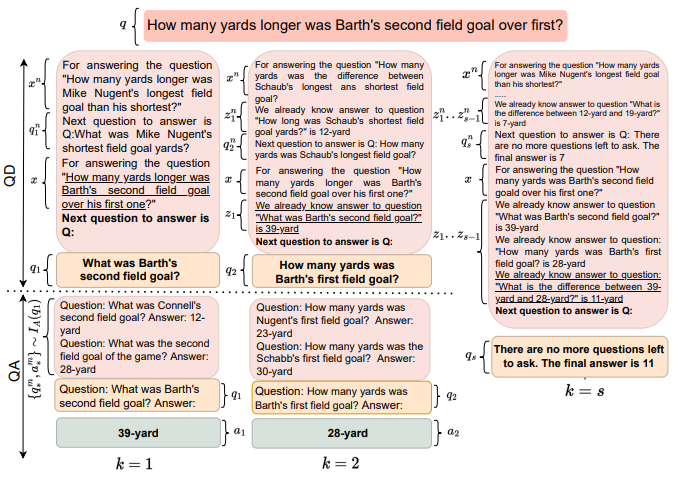
该方法还引入了一些数据集外的prompt示例的构造方式与一些符号化的构造方式,最终,在DROP数据集上取得了较高的准确率。
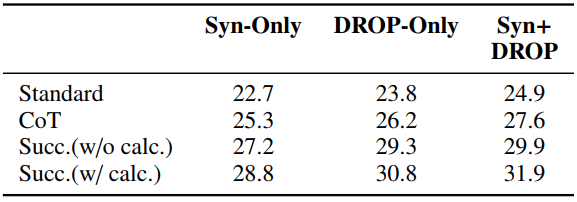
此外,论文的实验部分还比较了Prompting方法与Fine-tuning方法的效果,分别在问题分解部分和问题回答部分使用In-Context Prompting方法和Fine-tuning方法,我们可以看到Fine-tuning方法均带来了准确率提升。且在问题分解部分(QD)使用Fine-tuning会带来更大幅提升,这说明大预言模型“具有”回答简单的子问题的能力,问题分解是限制复杂推理准确率的“瓶颈”。
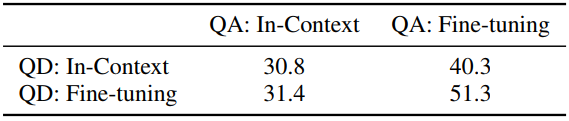

文章三:利用大预言模型解决知识图谱中的复杂逻辑推理问题[4]
知识图谱的复杂逻辑查询通常指一阶逻辑查询(First-Order Logical Queries),即由合取(conjunction, ∧),析取(disjunctions, ∨),存在量词(existential quantifiers, ∃)和非(negation, ¬)操作构成的逻辑语句。
在之前的工作中,复杂逻辑查询通常使用图表达学习的方法寻找答案,将节点、边和查询图都表达为低维向量空间中的某种形状,距离查询图的表达最近的节点即为查询的答案。但这类方法有以下三个缺点:一是对查询图的形式高度依赖,没有在训练集中出现过的查询图形式很难推断出正确的答案;二是泛化能力差,在一个图上训练的表达无法泛化到其他图;三是基于图表达的方法要求图的规模不能太大,而且对新加入的节点无法学习其表达。
因此,本文提出了一种基于大语言模型来回答知识图谱上一阶逻辑查询的方法LARK(Language-guided Abstract Reasoning over Knowledge graphs)。LARK通过查询中的实体和关系找到知识图谱中的相关子图作为上下文,利用大预言模型中农的prompting方法对分解后的query进行解答,具体的流程如下图。
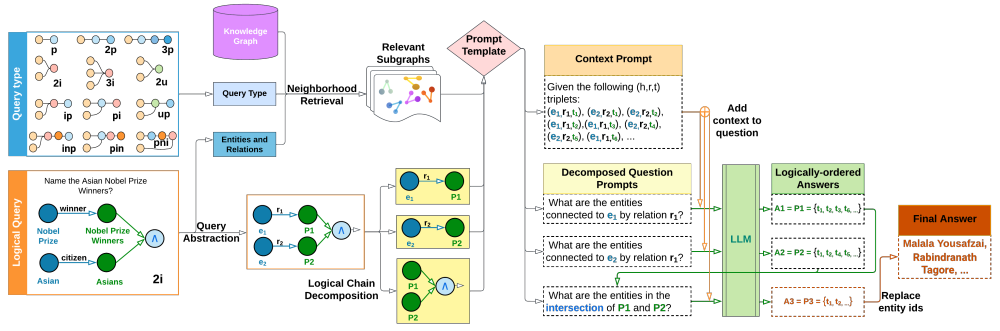
首先,Query Abstraction将所有的实体和关系都用ID来表示,以提高不同图谱和查询上的泛化能力。Neighborhood Retrieval将所有查询图中出现实体和关系的k跳内子图检索出来,作为上下文。
下一步,Logical Chain Decomposition将逻辑查询分解为一个子查询序列,利用k跳内的子图作为上下文提示词,按序回答每一个分解的子问题,最终得到查询的答案。
实验部分分为以下几个部分,分别解答下列问题。
问题1:LARK在复杂推理任务上的有效性
如下图,在大部分query形式中,LARK都是效果最好的方法。
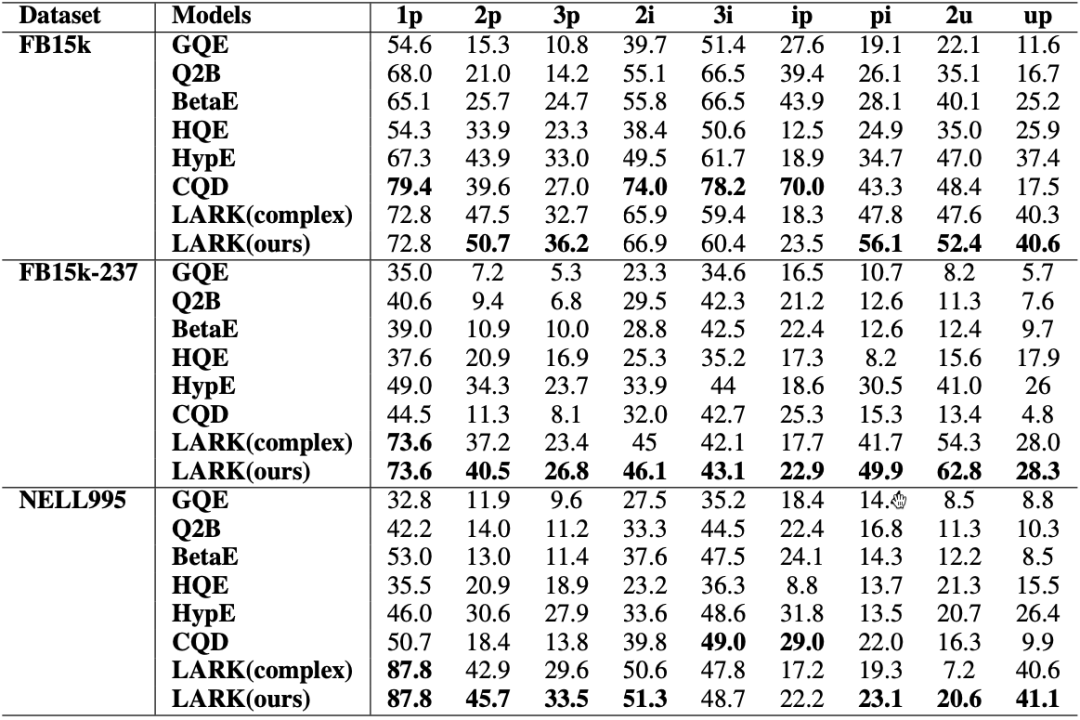
问题2:将查询图链式分解的优势
由上图,我们可以看到跳数多的查询下,LARK带来的效果提升更为明显。
问题3:大预言模型的规模对效果的影响
毋庸置疑,在所有的查询形式下,参数量更大的语言模型都会得到更好的表现。

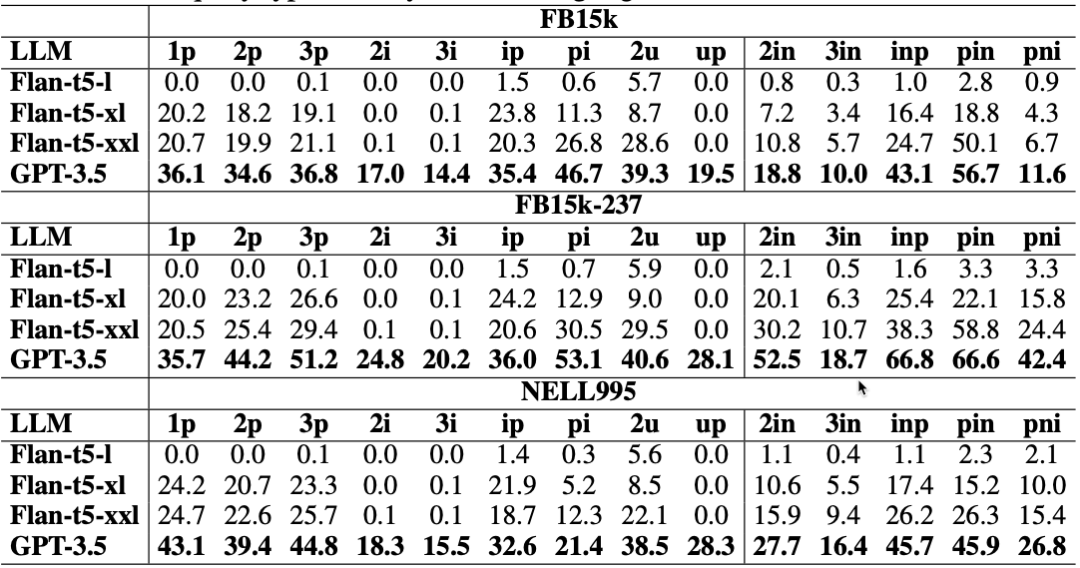
问题4:大预言模型Token数对效果的影响
在实验中,T5模型的token限制设置为2048,GPT-3.5的token限制为4096,实验选取了上下文token数大于2048的查询进行测试,由于模型学到的上下文更加丰富,这些查询使用更大token数的语言模型会得到更好的效果。
总 结
利用大语言模型解决自然语言复杂推理问题是近期的热点问题,将复杂问题拆解为易得到正确答案的子问题是其中的关键问题之一。知识图谱的逻辑查询图天然的有向无环图形式为复杂问题精准拆解为具有拓扑序的简单子问题序列带来了天然的优势。将大语言模型的推理能力与知识图谱的结构化知识融合,带来更好的推理能力是未来可能的研究方向。
参考文献
[1] J. Wei, X. Wang, D. Schuurmans, et al. (2022). Chain-of-thought prompting elicits reasoning in large language models. Advances in Neural Information Processing Systems.
[2] D. Zhou, N. Schärli, L. Hou, et al. (2023). Least-to-Most Prompting Enables Complex Reasoning in Large Language Models. The Eleventh International Conference on Learning Representations.
[3] D. Dua, S. Gupta, S. Singh, et al. (2022). Successive Prompting for Decomposing Complex Questions. Conference on Empirical Methods in Natural Language Processing.
[4] N. Choudhary, C. Reddy. (2023). Complex Logical Reasoning over Knowledge Graphs using Large Language Models. Arxiv.
)














)
)


)