目录
1.输出100以内3的倍数
2.将3个数从大到小输出
3.打印100~200素数
方法一
方法二
4.显示printf的返回值
最大公约数
试除法
辗转相除法
九九乘法表
求十个数的最大值
1.输出100以内3的倍数
法一：
int n = 0;
while (n*3 < 100){printf("%d ", n*3);n++;}法二：
int i = 0;for (i = 1; i <= 100; i++) {if (i % 3 == 0){printf("%d ", i);}}2.将3个数从大到小输出
由于只有3个数，我们可以采用中间变量换值的方法，相比于依次判断就显得很简单了。
int a = 0;int b = 0;int c = 0;int tmp = 0;scanf("%d %d %d", &a, &b, &c);if (a < c){tmp = c;c = a;a = tmp;}if (a < b){tmp = b;b = a;a = tmp;}if (b < c){tmp = b;b = c;c = tmp;}printf("%d %d %d\n", a, b, c);return 0;
}需要注意的是，这种办法改变了原变量的值。
3.打印100~200素数
方法一
素数，也称质数，特点是只能被1和自身整除，那我们是不是可以用2~n-1之间的数依次来取模进行判断呢？如果有一个数能被整除，那它就不是质数，反之是质数。
int i = 101;int n;for (i = 101; i < 200; i++){int flag = 0;//开关for (n = 2; n < i; n++){if (i % n == 0){flag = 0;break;}else flag = 1;}if(flag == 1)printf("%d ", i); }因为其中一个数不能整除并不代表它不是素数，所以我们设置一个开关，依次在真和假中切换，能整除为假，不能整除为真，遍历一遍后根据flag的值判断它是否为素数。
方法二
任意不是素数的数都可以分为 m*n的形式。
16 = 4*4
16 = 2*8
如果将这个数开平方，如果它不是素数，则在2~√n之间必定有个数使它的因子。
（例：√18 = 3(整形省略分数)
18 = 2*9 18 = 3*6 ）
大家想想是不是这样的道理，这样做可以减少遍历的次数。
#include <stdio.h>
#include<math.h>
int main(){int i = 101;int n;for (i = 101; i < 200; i+2){int flag = 0;for (n = 2; n <= sqrt(i); n++){if (i % n == 0){flag = 0;break;}else flag = 1;}if(flag == 1)printf("%d ", i); }
return 0;
}注意因子可以等于√n，sqrt是用来求根号的函数，需要包含头文件math.h
因为偶数不可能是素数，我们可以跳过偶数部分只进行奇数的循环。
4.显示printf的返回值
要求：第一行输入printf的输出值，第二行输出printf的返回值。
int ret = printf("hello world!");printf("\n%d", ret);
//等价于int ret = printf("\n%d", printf("hello world!"));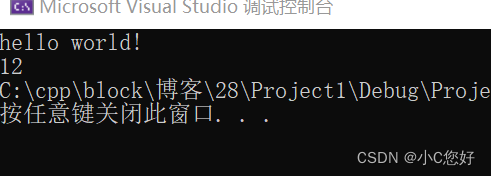 
由此我们可以得出结论：printf返回值是字符的个数
最大公约数
试除法
我们找到两个数中较小的那个，用它依次递减，如果能被这两个数整除，那它就是最大公约数。
int a = 0, b = 0;scanf("%d %d", &a, &b);int ret = a > b ? b : a;while (a % ret || b % ret){ret--;}printf("%d\n", ret);辗转相除法
具体来说就是两个数先求模，如果不等于0，被除数作为下一个除数，它们的模为新的被除数继续直到没有余数为止。
例如：24%12 = 0，则12就是最大公约数。25%12 = 1，12%1 = 0，1就是最大公约数。
反过来12%24 = 12，24%12 = 0，方法仍成立。
int a = 0, b = 0;int r = 0;scanf("%d %d", &a, &b);while (r = a % b){a = b;b = r;}printf("%d\n", b); 
附加题：如果要求最小公倍数该怎么做呢？
这里有个公式：最小公倍数 = 两数之积除以最大公约数（a*b/r）
九九乘法表
int i = 0;for (i = 1; i <= 9; i++){//打印一行int j = 0;for (j=1; j<=i; j++)//列数不超过行数{printf("%d*%d=%-2d ", i, j, i * j);}printf("\n");}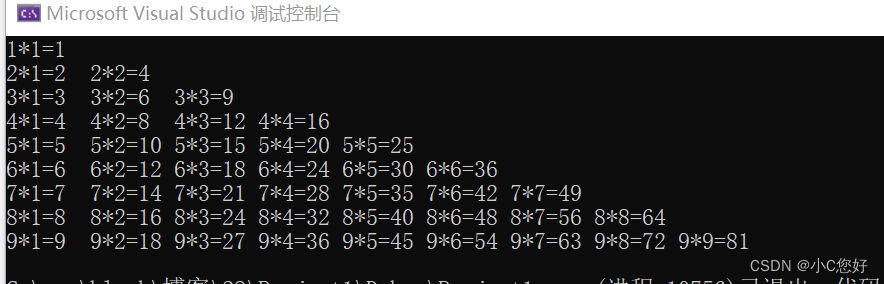
不多赘述，注意我们这里采用左对齐%-2d的方式，使得代码整齐,希望大家写代码的时候也能用到这样的技巧。
求十个数的最大值
这个没什么好说的，假定一个变量max遍历数组，选出最大值即可。需要注意的是，max只能是数组内的一个值，如果给它初始值为0，遇到负数可能会出现错误。
int arr[] = { -1,-2,-3,-4,-5,-6,-7,-8,-9,-10 };int max = arr[0];int i = 0;for (i = 1; i < 10; i++)//从第二个数开始{if (arr[i] > max)max = arr[i];}printf("%d\n", max);
