哈夫曼树
- 树的带权路径长度最小的二叉树
- WPL = 路径长度【边数】 * 结点权值
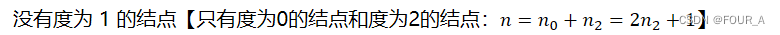
- n个叶结点的哈夫曼树共有 2n-1 个结点
- 哈夫曼树的任意非叶结点的左右子树交换后仍是哈夫曼树
- 对同一组权值,可能存在不同构的多棵哈夫曼树,但树的带权路径长度最小且唯一
- 哈夫曼树不一定是完全二叉树
哈夫曼编码
- 将字符频次作为字符结点权值,构造哈夫曼树,即可得哈夫曼编码,可用于数据压缩
- 不同频次的字符也可能在相同的层
- 前缀编码:没有一个编码是另一个编码的前缀
- 固定长度编码:每个字符用相等长度的二进制位表示
- 出现频次不同的字符一定在相同的层
- 可变长度编码:允许对不同字符用不等长的二进制位表示
哈夫曼m叉树
- 先补上权值为0结点,让序列凑可以构造m叉树的序列,每次挑最小m个去造树。

并查集
并查集的应用
- 判断联通性,计算连通分量的个数
- 判环
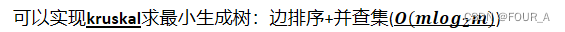
三要素:
- 初始化:初始化并查集, 将所有数组元素初始化为-1
- Find (S[],x):“查”, 找到元素x所属集合的根结点
Union (S[ ], root1, root2):“并”, 将两个集合合并为一个集合
- 存储方式:
- 逻辑:双亲表示法
- 物理:数组
- 时间复杂度:
- find:
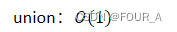
- 总复杂度:n个元素多次Union
- find:
不考虑并查集的代码题









)

详解)

的通信架构)





