222.完全二叉树的节点个数
给出一个完全二叉树,求出该树的节点个数。
示例 1:
输入:root = [1,2,3,4,5,6]
输出:6
示例 2:
输入:root = []
输出:0
示例 3:
输入:root = [1]
输出:1
提示:
树中节点的数目范围是[0, 5 * 10^4]
0 <= Node.val <= 5 * 10^4
题目数据保证输入的树是 完全二叉树
思路
参考:https://www.programmercarl.com/0222.%E5%AE%8C%E5%85%A8%E4%BA%8C%E5%8F%89%E6%A0%91%E7%9A%84%E8%8A%82%E7%82%B9%E4%B8%AA%E6%95%B0.html
普通二叉树的思路(时间复杂度为O(n))
直接采用遍历(以后序遍历为例)
直接采用前/中/后遍历,返回遍历结果(列表存储),然后列表的长度即为节点个数
此时,时间复杂度O(n) 因为要遍历到每个节点 空间复杂度O(H) H为树的高度 递归
递归
class TreeNode(object):def __init__(self, val=0, left=None, right=None):self.val = valself.left = leftself.right = right# 用遍历方法 时间复杂度O(n) 因为要遍历到每个节点 空间复杂度O(H) H为树的高度 递归
class Solution(object):def countNodes(self, root):""":type root: TreeNode:rtype: int"""result = self.post(root)return len(result)# 后序遍历def post(self, node):if not node:return []left = self.post(node.left)right = self.post(node.right)return left + right + [node.val]
迭代
后序遍历 迭代法
class Solution(object):def countNodes(self, root):""":type root: TreeNode:rtype: int"""if not root:return 0result = []stack = [root]while stack:node = stack.pop()result.append(node.val)if node.right:stack.append(node.right)if node.left:stack.append(node.left)return len(result)
递归法-直接求节点的数目 而不是遍历节点
切记递归法的三步
- 时间复杂度:O(n)
- 空间复杂度:O(log n)(完全二叉树的高度),算上了递归系统栈占用的空间
# 直接遍历求节点数目 时间复杂度O(n) 因为要遍历到每个节点 空间复杂度O(H) H为树的高度 递归
class Solution(object):def countNodes(self, root):""":type root: TreeNode:rtype: int"""return self.helper(root)def helper(self, node): # 递归第一步:确定参数和返回 参数就是传入节点 返回就是Intif not node:return 0 # 递归第二步:确定终止条件 当节点为空的时候 此时节点数目当然是0# 单层逻辑 左右中 依然是后序遍历leftnum = self.helper(node.left) # 左rightnum = self.helper(node.right) # 右return leftnum + rightnum + 1 # 中
完全二叉树的思路
这就需要考虑到完全二叉树的性质
在完全二叉树中,除了最底层节点可能没填满外,其余每层节点数都达到最大值,并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层,则该层包含 1~ 2^(h-1) 个节点。
大家要自己看完全二叉树的定义,很多同学对完全二叉树其实不是真正的懂了。
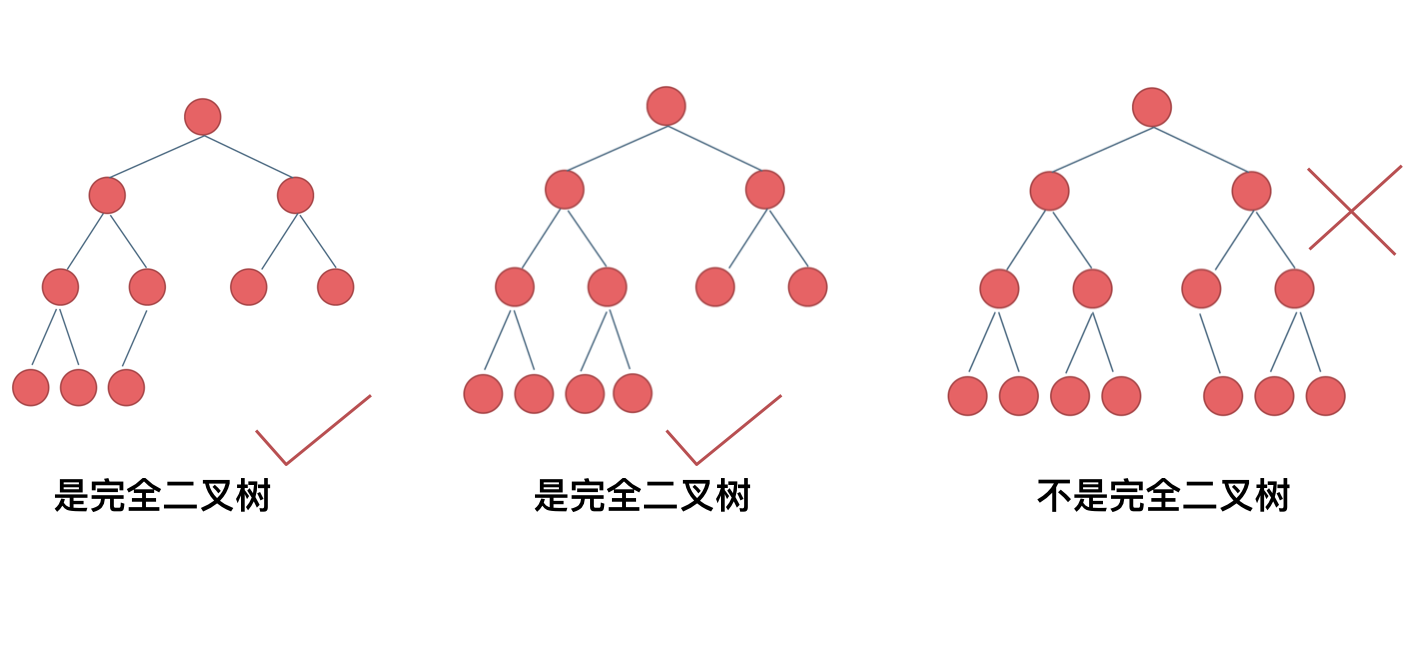
完全二叉树只有两种情况,情况一:就是满二叉树,情况二:最后一层叶子节点没有满。
对于情况一,可以直接用 2^树深度 - 1 来计算,注意这里根节点深度为1。
对于情况二,分别递归左孩子,和右孩子,递归到某一深度一定会有左孩子或者右孩子为满二叉树(重点),然后依然可以按照情况1来计算。
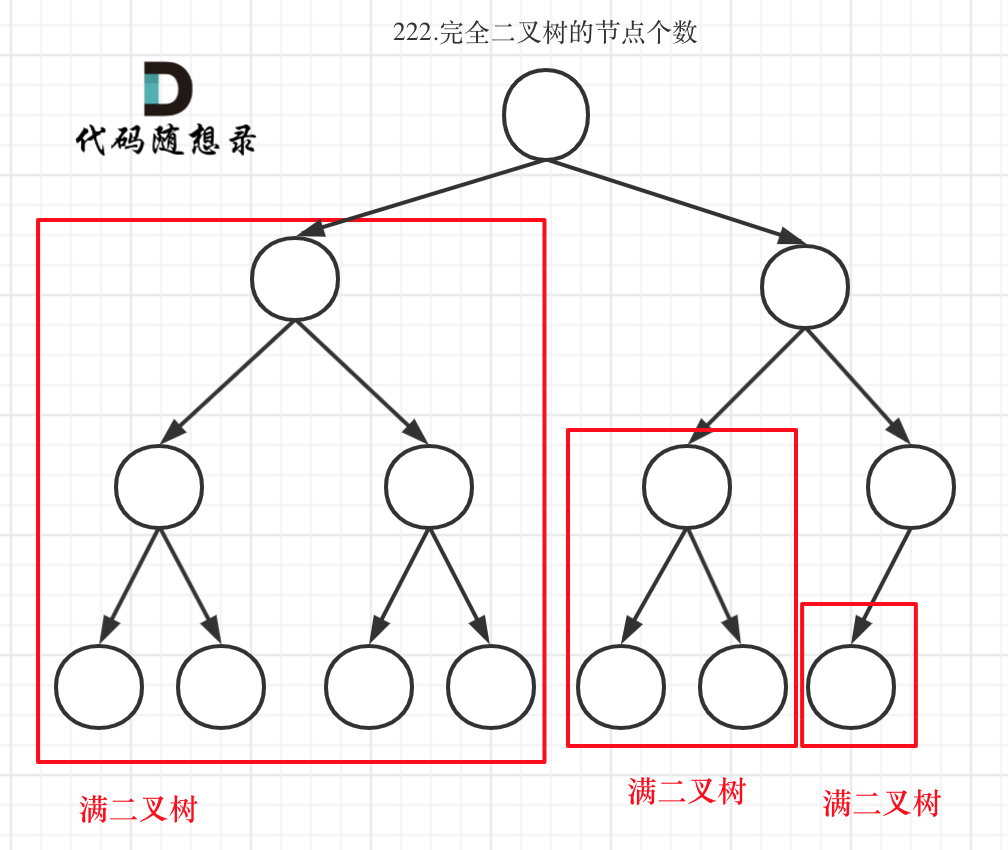
完全二叉树(一)如图:
完全二叉树(二)如图:
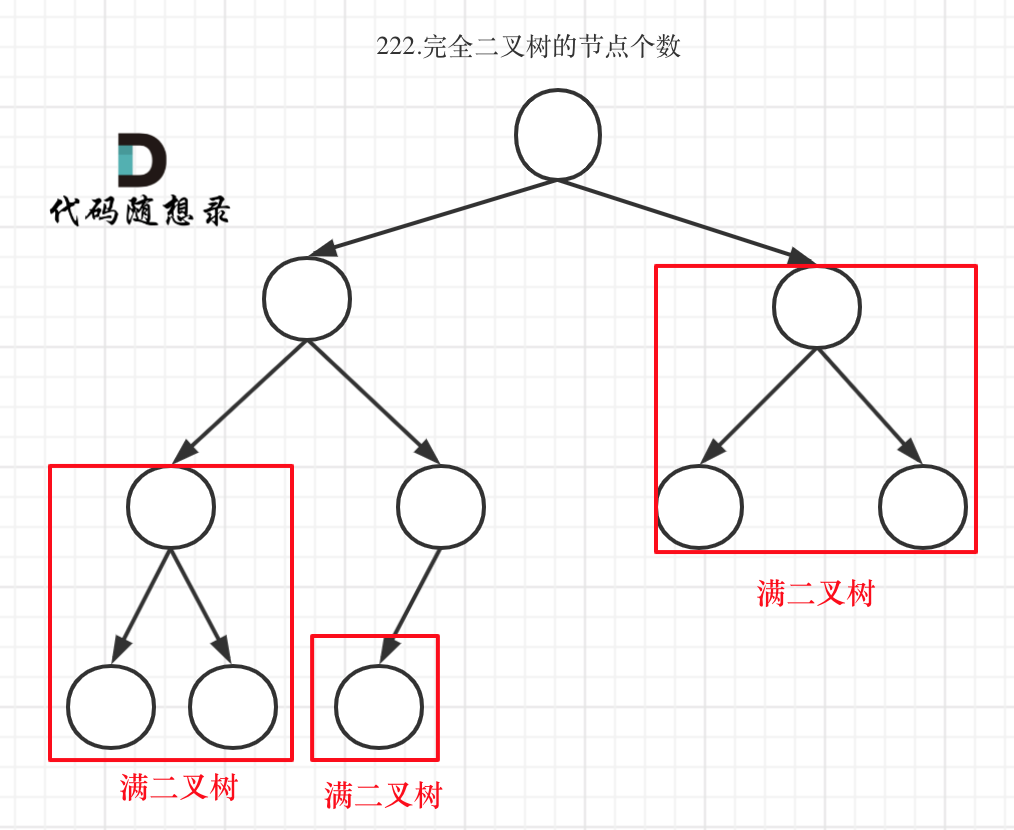
可以看出如果整个树不是满二叉树,就递归其左右孩子,直到遇到满二叉树为止,用公式计算这个子树(满二叉树)的节点数量。
这里关键在于如何去判断一个左子树或者右子树是不是满二叉树呢?
在完全二叉树中,**如果递归向左遍历的深度等于递归向右遍历的深度,那说明就是满二叉树。**如图:
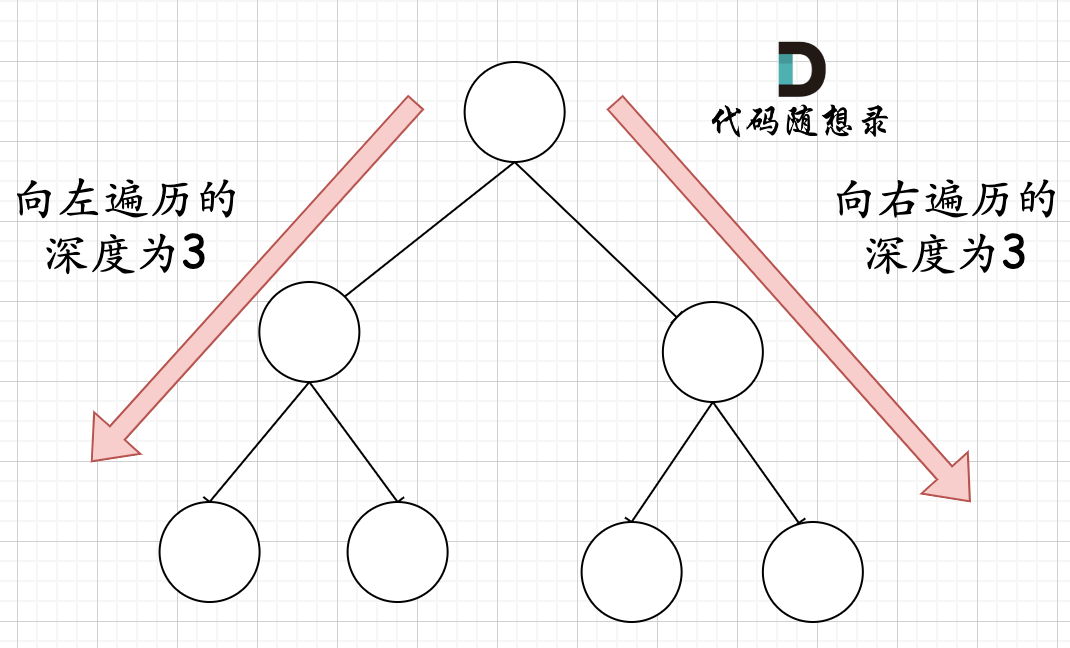
在完全二叉树中,如果递归向左遍历的深度不等于递归向右遍历的深度,则说明不是满二叉树,如图:
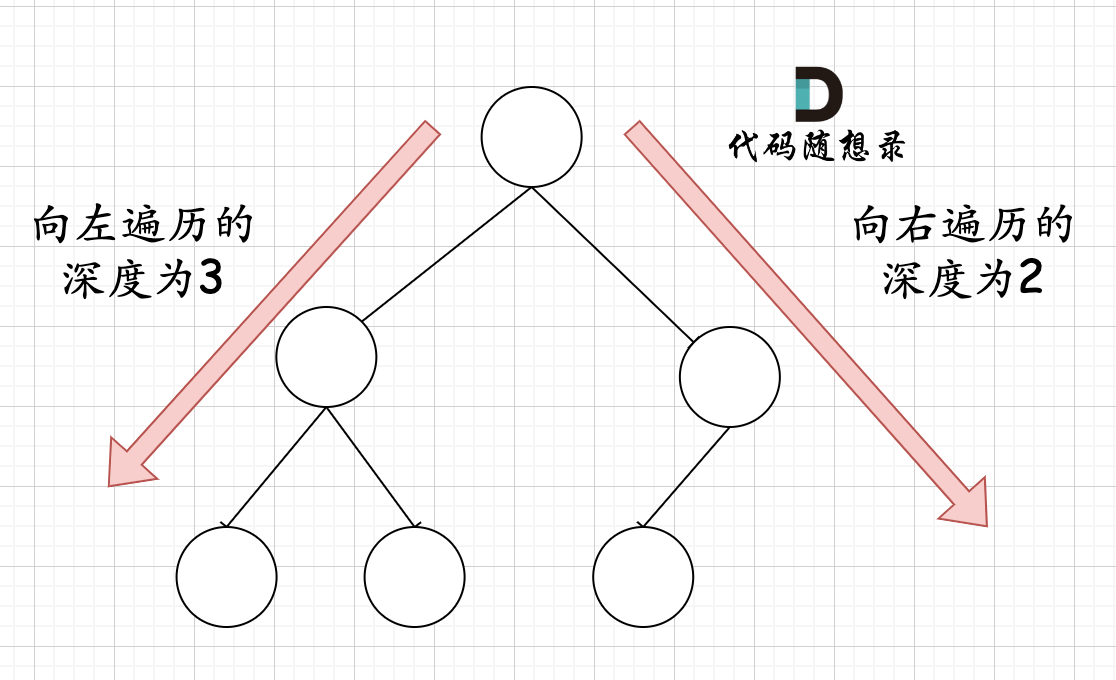
那有录友说了,这种情况,递归向左遍历的深度等于递归向右遍历的深度,但也不是满二叉树,如题:
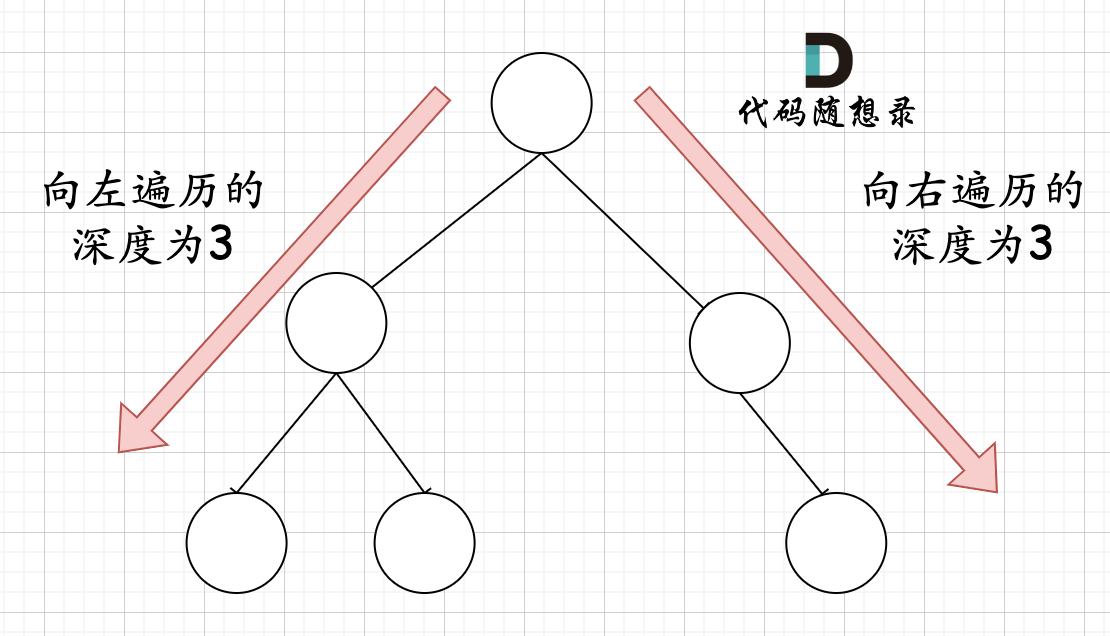
如果这么想,大家就是对 完全二叉树理解有误区了,以上这棵二叉树,它根本就不是一个完全二叉树!
所以采用递归来判断左右子树是不是满二叉树:
# 如何使用时间复杂度少于O(n)的方法?
# 以上都是普通二叉树的做法 如果熟悉完全二叉树的性质 那就可以使用时间复杂度更低的方法
class Solution(object):def countNodes(self, root):""":type root: TreeNode:rtype: int"""if not root:return 0left = root.leftright = root.rightleftdepth, rightdepth = 0, 0while left: # 求左子树深度left = left.leftleftdepth += 1while right: # 求右子树深度right = right.rightrightdepth += 1# 中if leftdepth == rightdepth: # 两边是满二叉树return (2<<leftdepth) - 1 # 为什么**不能return self.countNodes(root.left) + self.countNodes(root.right) + 1
参考:
https://www.programmercarl.com/0222.%E5%AE%8C%E5%85%A8%E4%BA%8C%E5%8F%89%E6%A0%91%E7%9A%84%E8%8A%82%E7%82%B9%E4%B8%AA%E6%95%B0.html




)









:Stable Diffusion文本条件生成图像大模型)

: Image Acquisition(图像加载))
)

