文档讲解:代码随想录
视频讲解:代码随想录B站账号
状态:看了视频题解和文章解析后做出来了
123.买卖股票的最佳时机III
class Solution:def maxProfit(self, prices: List[int]) -> int:if len(prices) == 0:return 0dp = [[0] * 5 for _ in range(len(prices))]dp[0][1] = -prices[0]dp[0][3] = -prices[0]for i in range(1, len(prices)):dp[i][0] = dp[i-1][0]dp[i][1] = max(dp[i-1][1], dp[i-1][0] - prices[i])dp[i][2] = max(dp[i-1][2], dp[i-1][1] + prices[i])dp[i][3] = max(dp[i-1][3], dp[i-1][2] - prices[i])dp[i][4] = max(dp[i-1][4], dp[i-1][3] + prices[i])return dp[-1][4]- 时间复杂度:O(n)
- 空间复杂度:O(n)
1. 确定dp数组以及下标的含义
这道题有点变态了,dp需要5个状态。
dp[i][0]代表一开始不持有股票的状态,1代表第一次持有,2代表第一次卖出后不持有的状态,3代表第二次持有,4代表第二次卖出后不持有的状态。
2. 确定递推公式
dp[i][1] = max(dp[i-1][1], dp[i-0] - prices[i])
dp[i][2] = max(dp[i-1][2], dp[i-1] + prices[i])
老样子,持有的时候递推为前一天持有状态下的现金和前一天不持有今天买入的现金之间的较大者。第一次卖出的状态递推为前一天此状态和前一天持有今天卖出之间的较大值。
第二次交易同理,就不再写一遍了。
3. dp数组的初始化
(1) 第0天持有股票,那肯定是买入,所以初始化为-prices[i]
(2) 第0天不持有股票,那就是什么也没干,初始化为0
第二次持有股票,和第一次一样初始化为-prices[i]
第二次不持有股票,其实就是买卖了两次,所以初始化为0
4. 遍历顺序
递推公式中有i-1,所以从前往后遍历
5. dp数组举例
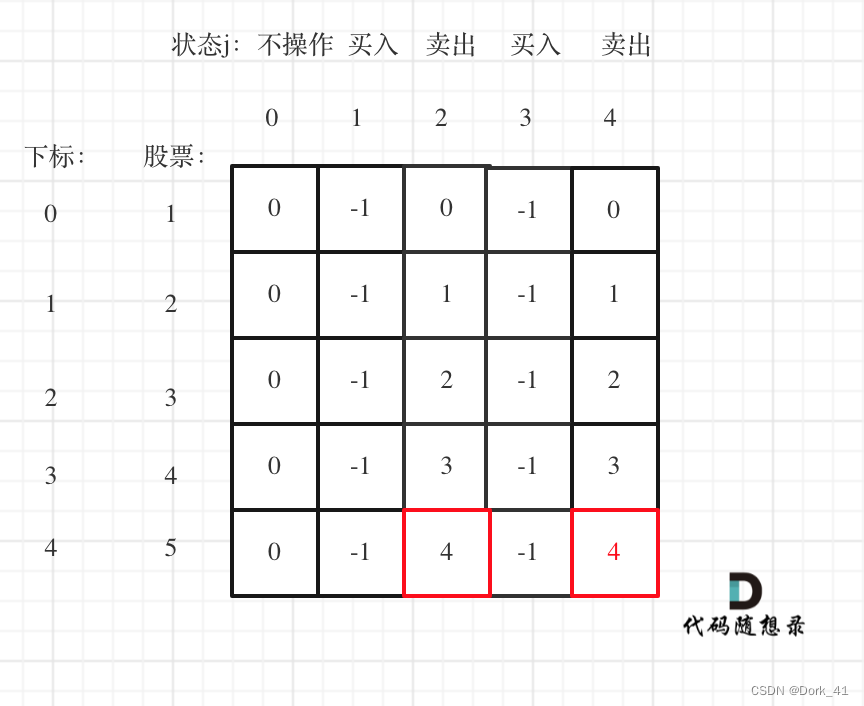
188.买卖股票的最佳时机IV
class Solution:def maxProfit(self, k: int, prices: List[int]) -> int:if len(prices) == 0:return 0dp = [[0]*(k*2+1) for _ in range(len(prices))]for i in range(k):dp[0][i*2+1] = -prices[0]for i in range(1, len(prices)):for j in range(k*2+1):if j == 0:dp[i][j] = dp[i-1][j]elif j % 2 == 1:dp[i][j] = max(dp[i-1][j], dp[i-1][j-1] - prices[i])else:dp[i][j] = max(dp[i-1][j], dp[i-1][j-1] + prices[i])return dp[-1][k*2]- 时间复杂度:O(n)
- 空间复杂度:O(n)
这题没啥好说的,就是上面那道题的变种,而且变得不是那么高明。
这次规定可以交易k次。那很简单啊,初始化和递归的index之前都是直接hardcode出来,这道题用一个for循环就行了。其他的全都一样。






,od查看)







)




灵笼人物识别)