目录
1、介绍
2、B+树特征
3、插入
4、删除
5、存储记录
1)方法1:按值存储
2)方法2:按引用存储
3)方法3:按引用列表存储
6、聚类(Clustering)
1)非聚类(Unclustered)
2)Clustered
7、计算 I/O 次数
8、批量加载
1、介绍
在之前我们讨论了不同的文件和记录表示方法,用于数据存储。本文将介绍索引,它是在数据文件之上运行的一种数据结构,有助于加速对特定键的读取。
我们可以将数据文件视为书籍的实际内容,将索引视为用于快速查找的目录。我们使用索引来使查询运行更快,特别是那些经常运行的查询。
考虑一个Web应用程序,在登录过程中根据用户名查找 Users 表中用户的记录。在用户名列上建立索引将通过快速找到尝试登录的用户的行来加速登录过程。
学习B+树(一种特定类型的索引)。以下是B+树的一个示例:
2、B+树特征
- 数字 d 是 B+ 树的阶数。每个节点(除了根节点)的条目数量必须满足 d ≤ x ≤ 2d,假设没有删除操作发生(如果删除数据,则叶节点最终可能少于 d 个条目)。每个节点内的条目必须排序。
- 在每个内部节点的条目之间,有一个指向子节点的指针。由于一个节点最多有 2d 个条目,内部节点最多可能有 2d+1 个子指针。这也被称为树的扇出度(tree’s fanout)。
- 位于一个内部节点条目左侧的子节点的键必须小于该条目,而位于右侧的子节点的键必须大于或等于该条目。
- 所有叶节点都具有相同的深度,并且具有 d 到 2d 个条目(即至少半满)。
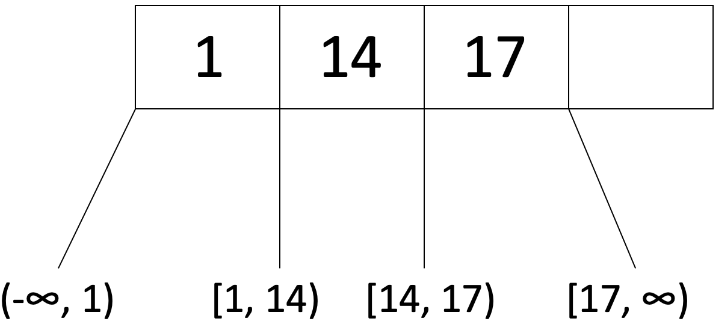
例如,这是一颗阶数 d=2 的树的节点:
请注意,该节点满足阶数要求,也称为(the occupancy invariant )占用不变式(d ≤ x ≤ 2d),因为在这里 d=2,而该节点有 3 个条目,满足 2 ≤ x ≤ 4。
- 由于排序和子节点的属性,我们可以沿着树向下遍历到叶节点,以找到我们需要的记录。这类似于二叉搜索树(BSTs)。
- 每个从根到叶子的路径具有相同数量的边 - 这就是树的高度。从这个意义上说,B+树始终是平衡的。换句话说,只有具有根节点的B+树的高度为0。
- 只有叶节点包含记录(或记录的指针 - 这将在后面解释)。内部节点(非叶节点)不包含实际的记录。
例如,这是一颗阶数 d=1 的树:
3、插入
将条目(节点)插入 B+ 树,可按照以下步骤进行:
a. 找到要插入值的叶节点 L。您可以通过沿树向下遍历来完成。按顺序将键和记录添加到叶节点。
b. 如果 L 溢出(即 L 有超过 2d 个条目)
- 将其分为 L_1 和 L_2。在 L_1 中保留 d 个条目(这意味着 d+1 个条目将放在 L_2 中)。
- 如果 L 是叶节点,将 L_2 的第一个条目复制到父节点。如果 L 不是叶节点,则将 L_2 的第一个条目移动到父节点。
- 调整指针。
c. 如果父节点溢出,那么对其进行递归,即对父节点执行步骤 2。(这是唯一会增加树高度的情况)
注意:我们想要将叶节点数据复制到父节点,这样我们就不会丢失叶节点中的数据。请记住,建立索引的表中的每个键都必须在叶节点中!在内部节点中的键并不意味着该键实际上仍然存在于表中。另一方面,我们可以将内部节点数据移动到父节点,因为内部节点并不包含实际的数据,它们只是在遍历树时引导搜索的引用。
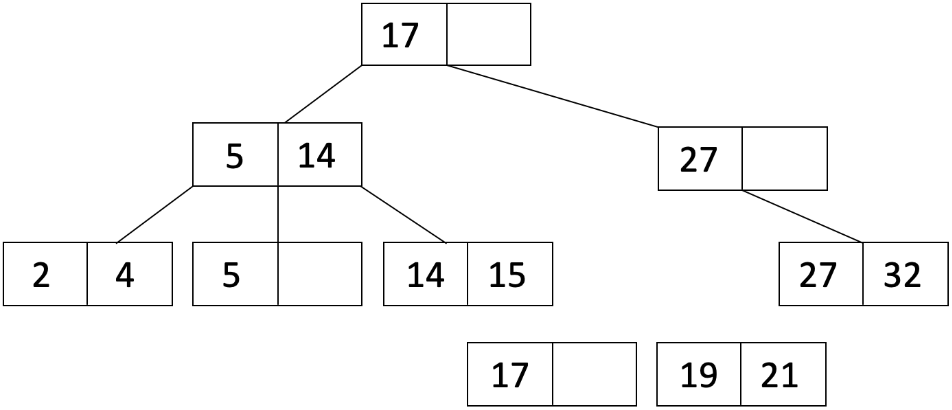
让我们通过一个例子来更好地理解这个过程!我们从以下的阶数为 d=1 的树开始:
让我们将 19 插入到我们的树中。当我们插入 19 时,我们看到在具有 17 的叶节点中有空间:
现在让我们将 21 插入到我们的树中。当我们插入 21 时,它导致一个叶节点溢出。因此,我们将这个叶节点分割成两个如下所示的叶节点:
L_1 是具有 17 的叶节点,而 L_2 是具有 19 和 21 的叶节点。
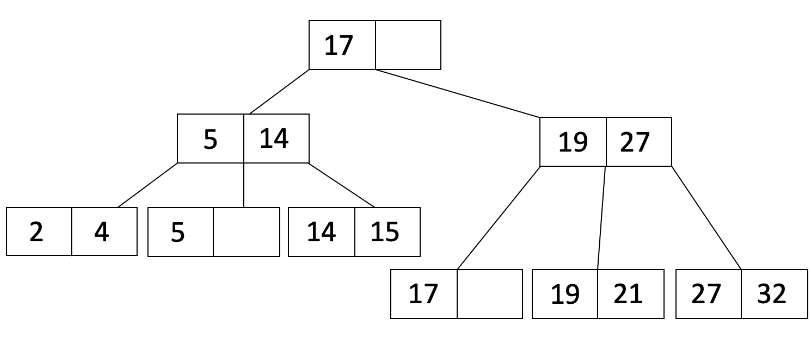
由于我们分割了一个叶节点,我们将 L_2 的第一个条目复制到父节点,并调整指针。我们还对父节点的条目进行排序,得到:
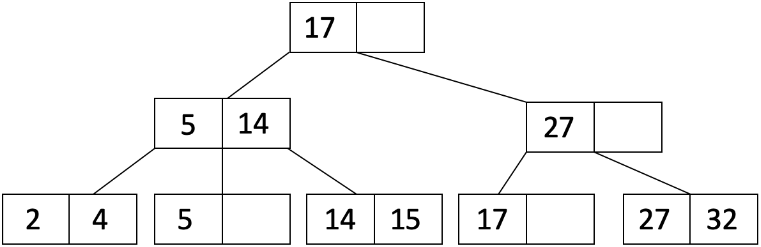
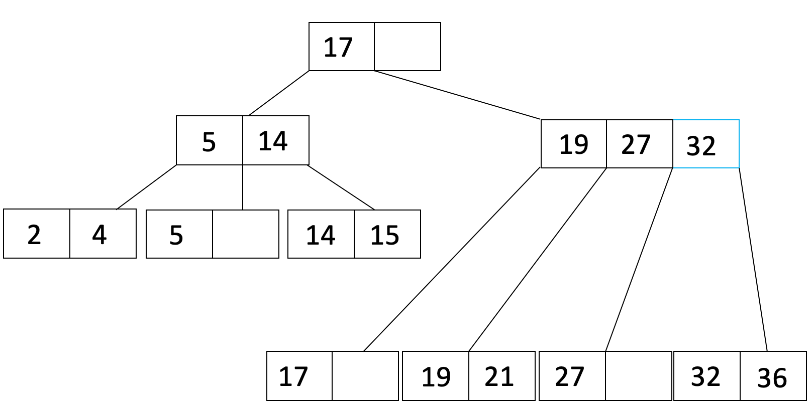
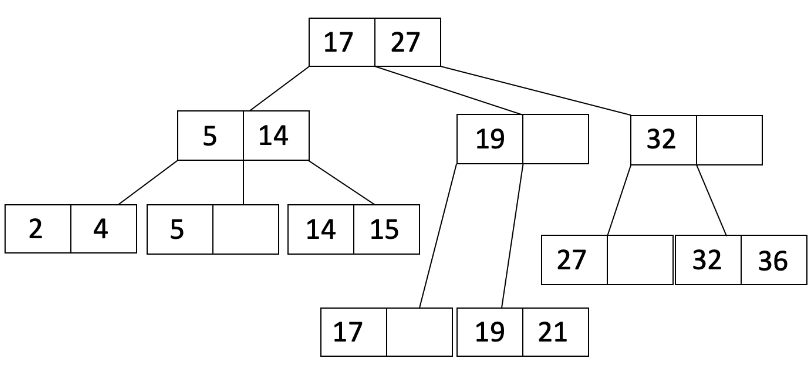
让我们再进行一次插入。这次我们将插入 36。当我们插入 36 时,叶节点溢出,因此我们将执行与插入 21 时相同的过程,得到:
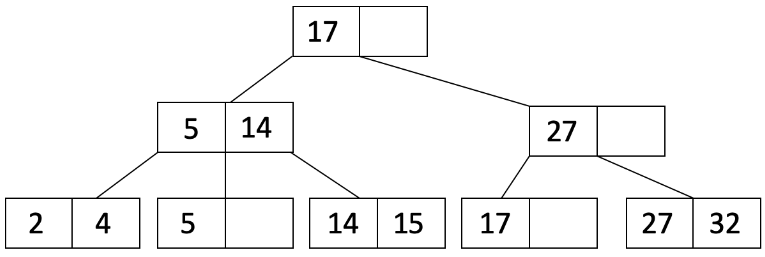
请注意,现在父节点溢出了,因此我们现在必须进行递归。我们将分割父节点,得到:
L_1 是具有 19 的内部节点,而 L_2 是具有 27 和 32 的内部节点。
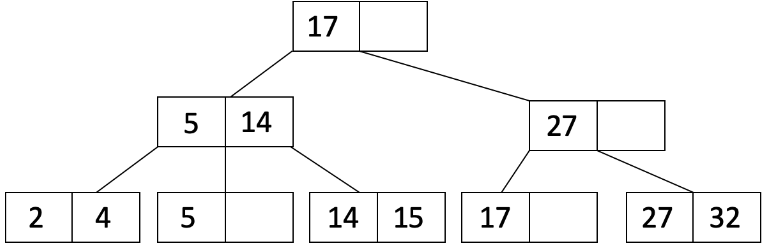
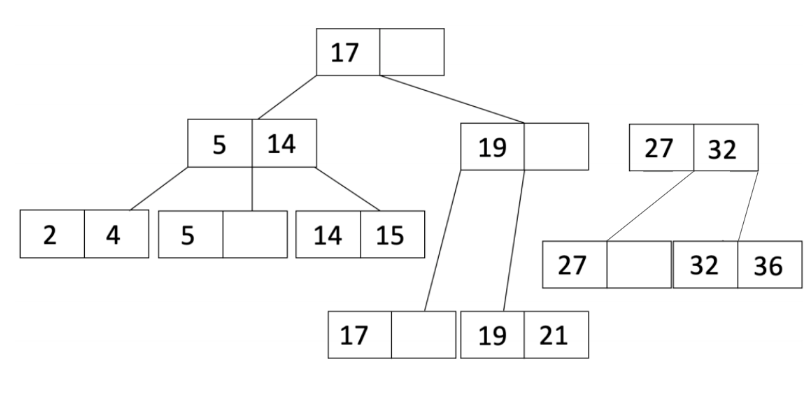
由于溢出的是内部节点,我们将 L_2 的第一个条目移动到父节点,并调整指针,得到:
最后,以下是关于插入B+树的一些建议说明:
通常,B+ 树节点具有至少 d 个条目和最多 2d 个条目。换句话说,如果树中的节点在插入之前满足这个不变性(通常会满足),那么插入后,它们将继续满足这个不变性。
当节点包含超过 2d 个条目时,发生插入溢出。
4、删除
要删除一个值,只需找到适当的叶节点,并从该叶节点中删除不需要的值。就是这么简单。(是的,从技术上讲,我们可能会违反一些 B+ 树的不变性。这没关系,因为在实践中,我们进行的插入比删除多得多,因此删除的内容很快就会被替换。)
提醒:我们永远不会删除内部节点的键,因为它们只用于搜索而不是保存数据。
5、存储记录
直到现在,我们还没有讨论过记录实际上是如何存储在叶节点中的。现在让我们来看看。有三种在叶节点中存储记录的方法:
1)方法1:按值存储
在方法1中,叶子页面就是数据页面。与其包含指向记录的指针,不如说叶子页面包含记录本身。
虽然方法 1 是可能最简单的实现方式,但它有一个重要的限制:如果我们只有方法1,就不能支持在同一文件上构建多个索引(在上面的例子中,我们不能在 'name' 上支持二级索引。相反,我们必须复制文件并在该文件上构建一个新的方法 1 索引。
2)方法2:按引用存储
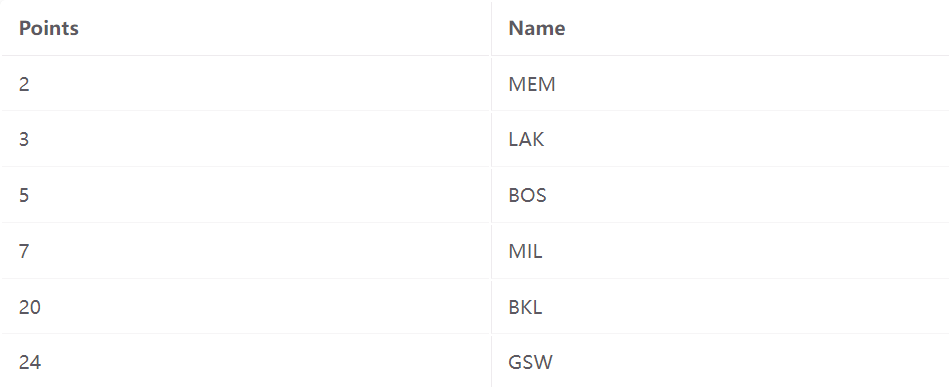
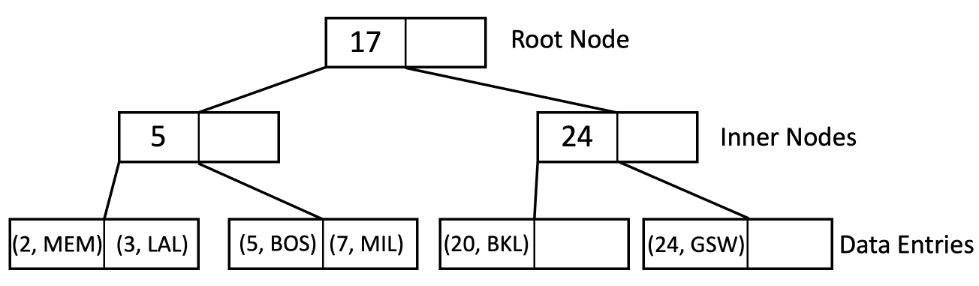
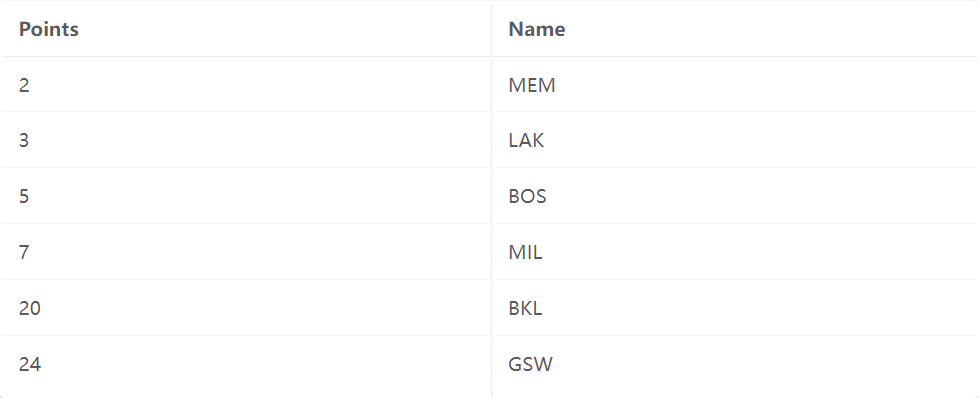
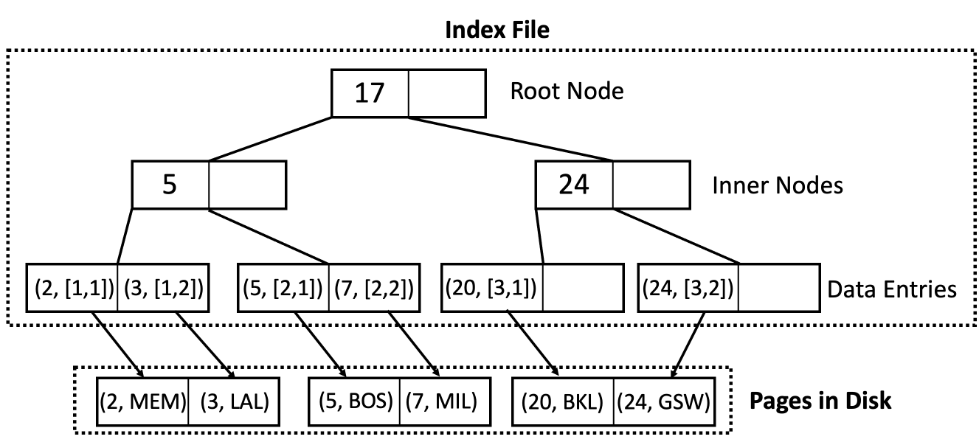
在方法 2 中,叶子页面保存指向相应记录的指针。
符号说明:在上面的图表中,叶节点包含(Key,RecordID)对,其中 RecordID 是 [PageNum,RecordNum]。
按引用进行索引允许我们在同一文件上拥有多个索引,因为实际数据可以以任何顺序存储在磁盘上。
3)方法3:按引用列表存储
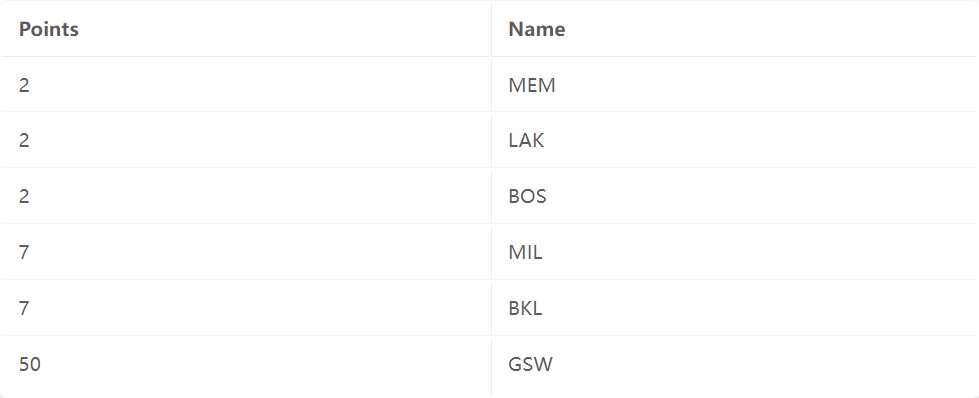
在方法 3 中,叶节点保存指向相应记录的指针列表。与方法 2 相比,当同一叶节点条目存在多个记录时,这种方式更紧凑。现在,每个叶节点包含(Key,RecordID列表)对。
6、聚类(Clustering)
现在我们已经讨论了记录如何存储在叶节点中,我们还将讨论数据页上的数据如何组织。 集群/非集群是指数据页的结构方式。 由于叶页是方法1 的实际数据页,并且键在索引叶页上排序,因此方法1 索引默认情况下是聚集的。 因此,去聚类仅适用于方法 2 或 3。
1)非聚类(Unclustered)
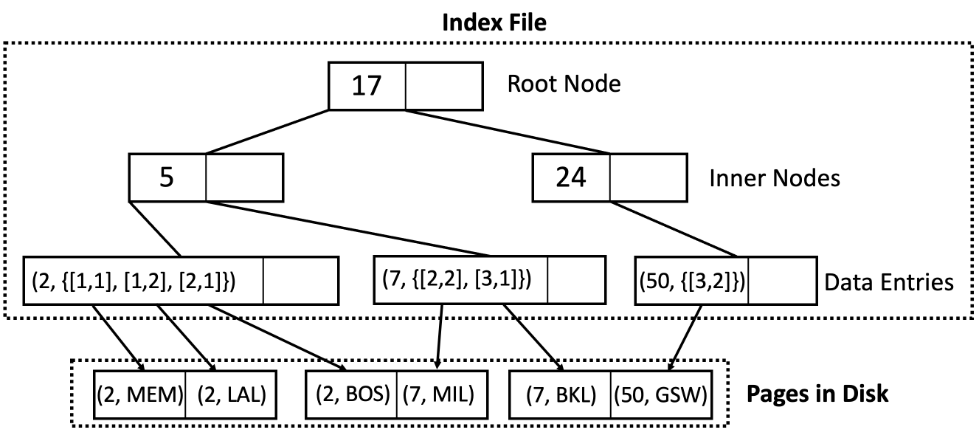
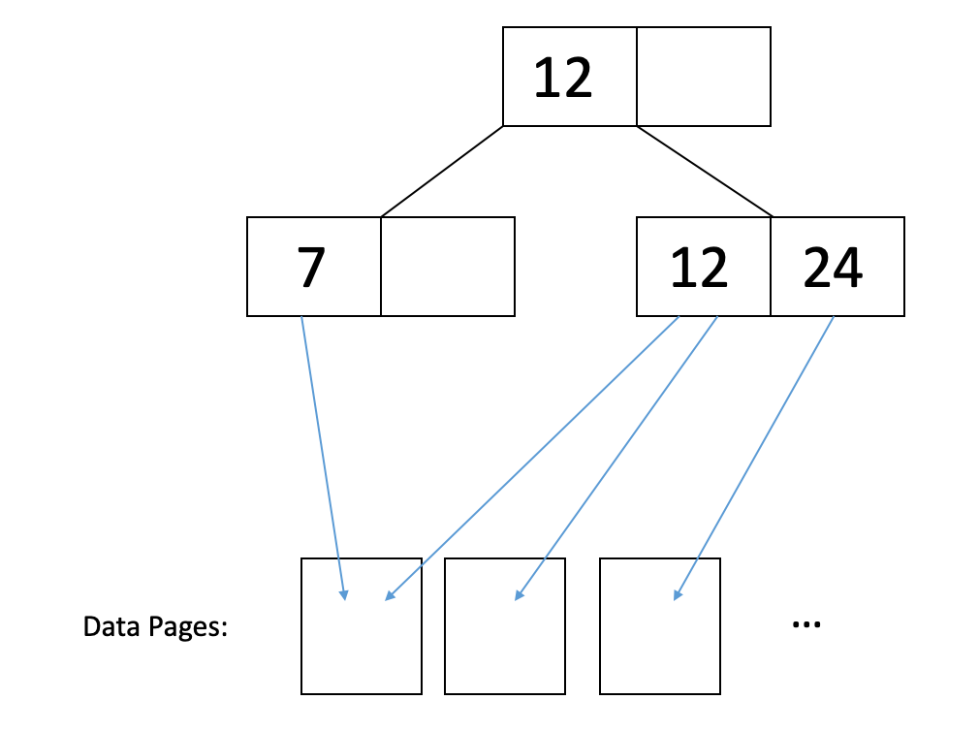
在非聚类索引中,数据页面是完全混乱的。因此,很可能你需要为每个你想要的记录读取一个单独的页面。例如,考虑这个图示:
在上面的图中,如果我们想要读取键为12和24的记录,那么我们必须分别读取它们指向的每个数据页面,以检索与这些键关联的所有记录。
2)Clustered
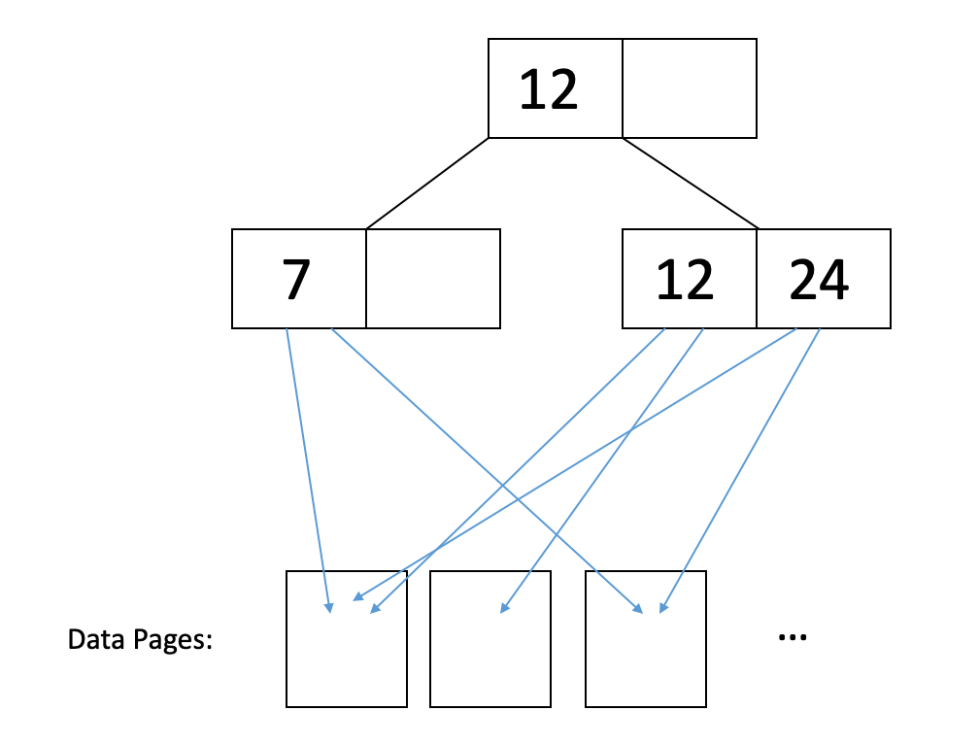
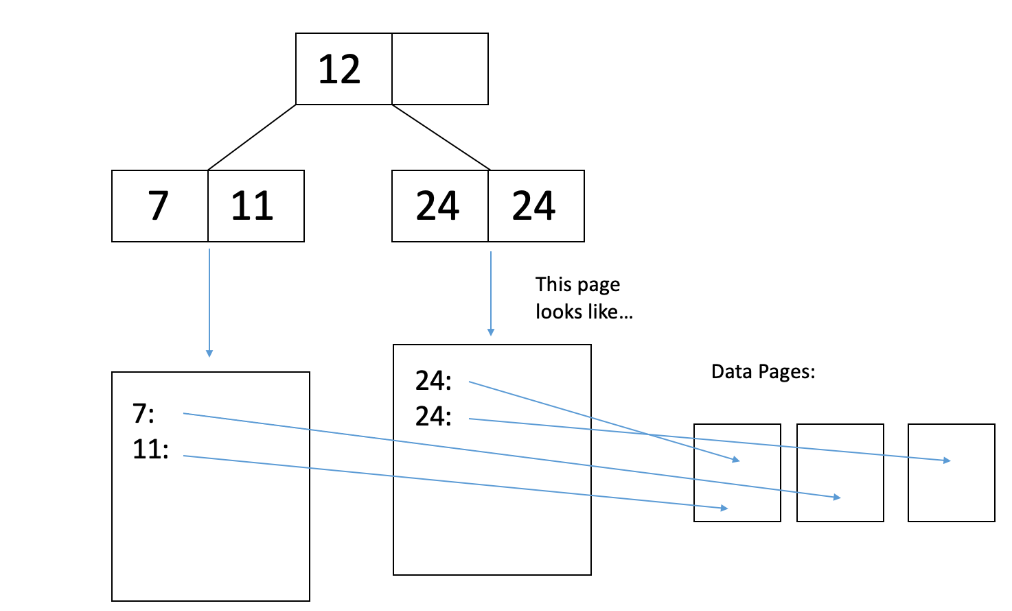
在聚类索引中,数据页面按照构建 B+ 树时使用的相同索引进行排序。这并不意味着数据页面是精确排序的,只是键大致按照数据的顺序排列。因此,I/O成本的差异主要来自缓存,其中具有接近键的两个记录可能在同一页,因此可以从缓存的页面中读取第二个记录。因此,通常只需要读取一页即可获取具有公共/相似键的所有记录。例如,考虑这个图示:
在上面的图中,我们可以通过读取 2 页来读取键为 7 和 12 的记录。如果我们按照叶节点值的顺序进行顺序读取,数据页面基本相同。因此,总的来说:
- 非聚类 = 每条记录 ~ 1 次 I/O。
- 聚类 = 每页记录 ~ 1 次 I/O。
- 聚类 vs 非聚类索引:尽管聚类索引在范围搜索方面可能更有效,并在顺序磁盘访问和预取等方面提供潜在的局部性优势,但它们通常比非聚类索引维护成本更高。例如,随着越来越多的插入操作,数据文件可能变得不太聚类,因此需要定期对文件进行排序。
7、计算 I/O 次数
以下是一般的步骤。这是值得记录的:
1. 读取适当的从根到叶子的路径。
2. 读取适当的数据页面。如果我们需要读取多个页面,我们将为每个页面分配一次读取 I/O。此外,我们需要考虑 Alt. 2 或 3 的聚类情况(见下文)。
3. 如果要修改数据页面,则写入数据页面。同样,如果我们要执行跨多个数据页面的写入,我们需要为每个页面分配写入 I/O。
4. 更新索引页面。
让我们看一个例子。请参考以下的 Alternative 2 非聚类 B+ 树:
我们想要从数据库中删除唯一的 11 岁。这将需要多少次I/O?
1、每个 2 个相关的索引页面(索引页面是内部节点或叶节点)需要 1 次I/O。
2、读取 11 岁记录所在的数据页面需要 1 次 I/O。一旦它在内存中,我们可以从页面中删除记录。
3、将修改后的数据页面写回磁盘需要 1 次 I/O。
4、现在我们的数据库中没有 11 岁了,我们应该从 B+ 树的叶页面中删除键 "11",这是在步骤 1 中已经读取的。我们这样做,然后将修改后的叶页面写回磁盘需要 1 次 I/O。因此,删除记录的总成本是 5 次 I/O。
8、批量加载
我们之前讨论的插入过程适用于对现有 B+ 树进行添加操作。然而,如果我们要从头开始构建一个 B+ 树,我们可以做得更好。这是因为如果我们使用插入过程,每次插入新内容时都必须遍历整棵树;对随机数据页面的常规插入也会导致缓存效率低和叶节点的利用率低,因为它们通常是半空的。相反,我们将使用批量加载:
1、对将建立索引的键进行排序。
2、填充叶节点,直到达到某个填充因子 f。注意,填充因子仅适用于叶节点。对于内部节点,我们仍然遵循相同的规则去插入,直到它们被填满。
3、从父节点到叶节点添加指针。如果父节点溢出,我们将执行与插入类似的过程。我们将父节点分成两个节点:
- 在 L_1 中保留 d 个条目(这意味着 d+1 个条目将进入 L_2)。
- 由于父节点溢出,我们将 L_2 的第一个条目移动到父节点。
- 调整指针。
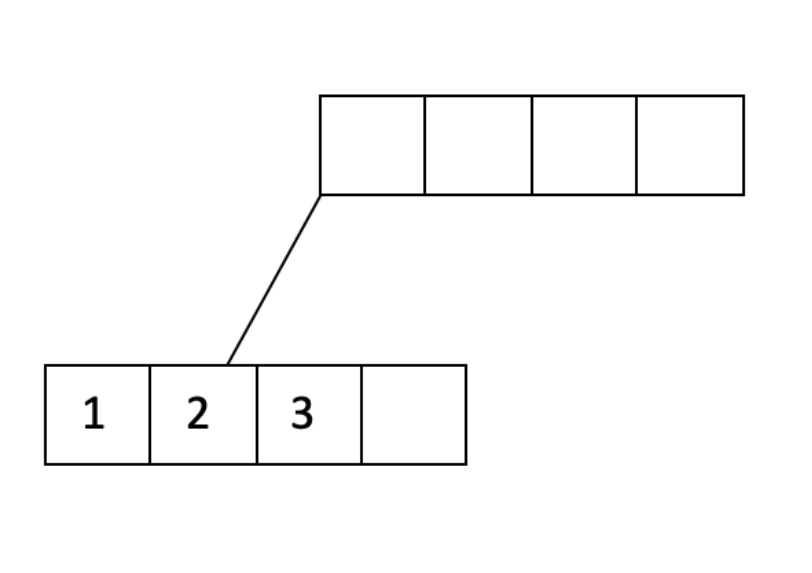
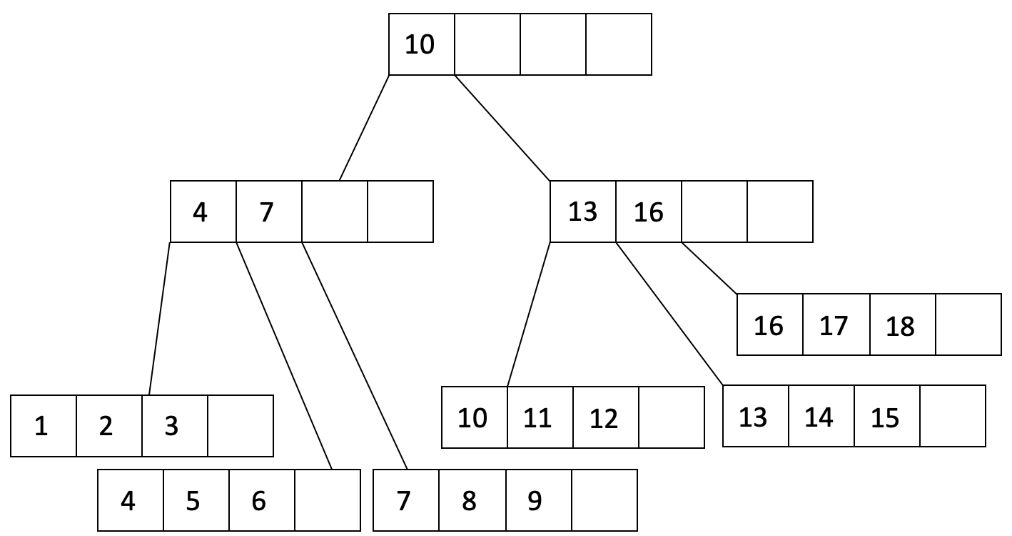
让我们看一个例子。假设我们的填充因子是 3/4,我们想要将 1 到 20 插入到一个顺序 d=2 的树中。我们将从填充叶节点开始,直到达到填充因子:
我们已经将一个叶节点填充到填充因子的 3/4,并从父节点添加了一个指向叶节点的指针。让我们继续填充:
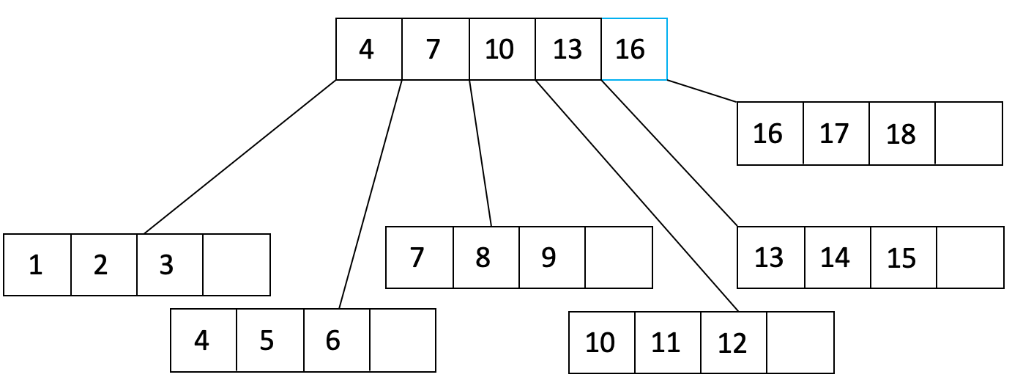
在上面的图中,我们看到父节点已经溢出。我们将父节点分成两个节点,并创建一个新的父节点:
从上面的例子中可以看出,通过批量加载构建的索引始终以聚类方式开始,因为底层数据是根据键排序的。为了保持聚类,我们可以根据未来的插入模式选择填充因子。
以上,DBS note2:DIsks and Files
祝好。




Vue2到Vue3)



)

顺利圆满举行)
——指令 directive)



公司的新产品开发流程(一))




