近期因俗事缠身，《通过理解LSTM的反向传播过程，理解LSTM解决梯度消失的原理 - 逐条解释LSTM创始论文全部推导公式，配超多图帮助理解》的中下篇鸽了实在太久有些不好意思了。为了避免烂尾，还是抽时间补上（上篇在此）。本文承接上篇，继续就Sepp Hochreiter 1997年的开山大作 Long Short-term Memory 中APPENDIX A.1和A.2所载的数学推导过程进行详细解读。希望可以帮助大家理解了这个推导过程，进而能顺利理解为什么那几个门的设置可以解决RNN里的梯度消失和梯度爆炸的问题。一家之言，若有任何错漏欢迎大家评论区指正。好了，Dig in！

上篇文章最后讲到了LSTM中记忆单元的激活状态关于各权重值的求偏导公式（公式15）。这里我们将从公式16开始。

5. 后向传播过程

前面介绍了那么多截断求导，后向传播过程将应用这些经过截断处理的求导公式来计算每个权重的误差值。

5.1 总误差

总误差是指输出单元在第 $t$ 时刻的输出值与目标值之间的方差。我们设 $t$ 时刻目标值为 $t^k(t)$ 。则有：
$\sum_{k:\ k\ output\ unit} (t^k(t) - y^k(t))^2 \tag{16},$
其中 $y^k(t)$ 是输出单元在 $t$ 时刻的激活值（参考公式6）。
在 $t$ 时刻，各权重值的梯度（记为 $\Delta w_{lm}(t)$ ）计算公式为：
$\Delta w_{lm}(t) = - \alpha \frac{\partial E(t)}{\partial w_{lm}} \tag{17}.$
其中 $\in \{ k, c_{j},in_{j},out_{j}, i\}$ ，分别代表输出单元 $k$ ，记忆单元 $c_{j}$ ，输入门 $in_{j}$ ，输出门 $out_{j}$ 及隐藏单元 $i$ 。 $\alpha$ 为学习率（learning rate），用于控制学习步进，如果学习步进过大，在遇到悬崖时很可能会一下把权重更新太多，跳跃到很远的地方(over shoot)，如果学习率太小，影响训练速度。
我们把不同单元和门在 $t$ 时刻的误差公式定义为：
$e_l(t) := - \frac{\partial E(t)}{\partial net_l(t)}\tag{18}.$

5.2 输出单元误差计算

令 $l = k$ ，我们通过式18可以得到输出单元在 $t$ 时刻的误差：
$\begin{aligned} e_k(t) &= - \frac{\partial E(t)}{\partial net_k(t)}\\ &= - \frac{\partial E(t)}{\partial y^k} * \frac{\partial y^k}{\partial net_k(t)}\\ &= - f'(net_k(t))*2(t^k(t) - y^k(t))*(-1 )\\ &= 2f'(net_k(t))(t^k(t) - y^k(t)) \end{aligned}$
我们把上边这个式子前面前边的常数 $2$ 让 $\alpha$ 吸收掉，就可以得到式19：
$e_k(t) = f'(net_k(t))(t^k(t) - y^k(t))\tag{19}$

下图为输出单元的梯度传播示意图：
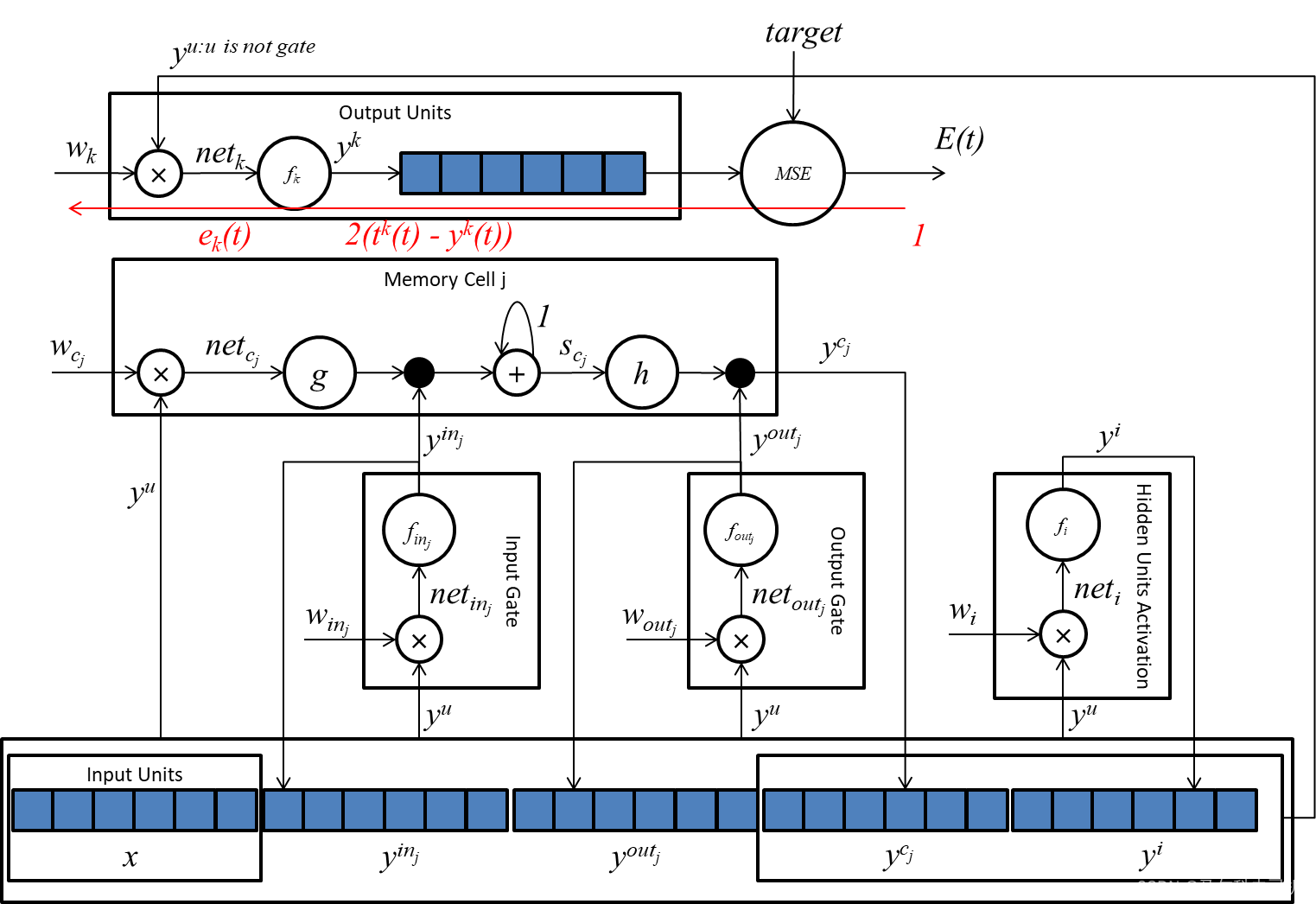
在这里插入图片描述

5.3 隐藏单元误差计算

令 $l = i$ ，我们可以得到隐藏单元在 $t$ 时刻的误差：
$\begin{aligned} e_i(t) &= - \frac{\partial E(t)}{\partial net_i(t)}\\ &= f_i'(net_i(t))\sum_{k:\ k\ output\ unit}w_{ki}e_k(t)\tag{20}\\ \end{aligned}$

下图显示了隐藏单元的梯度传播路线：
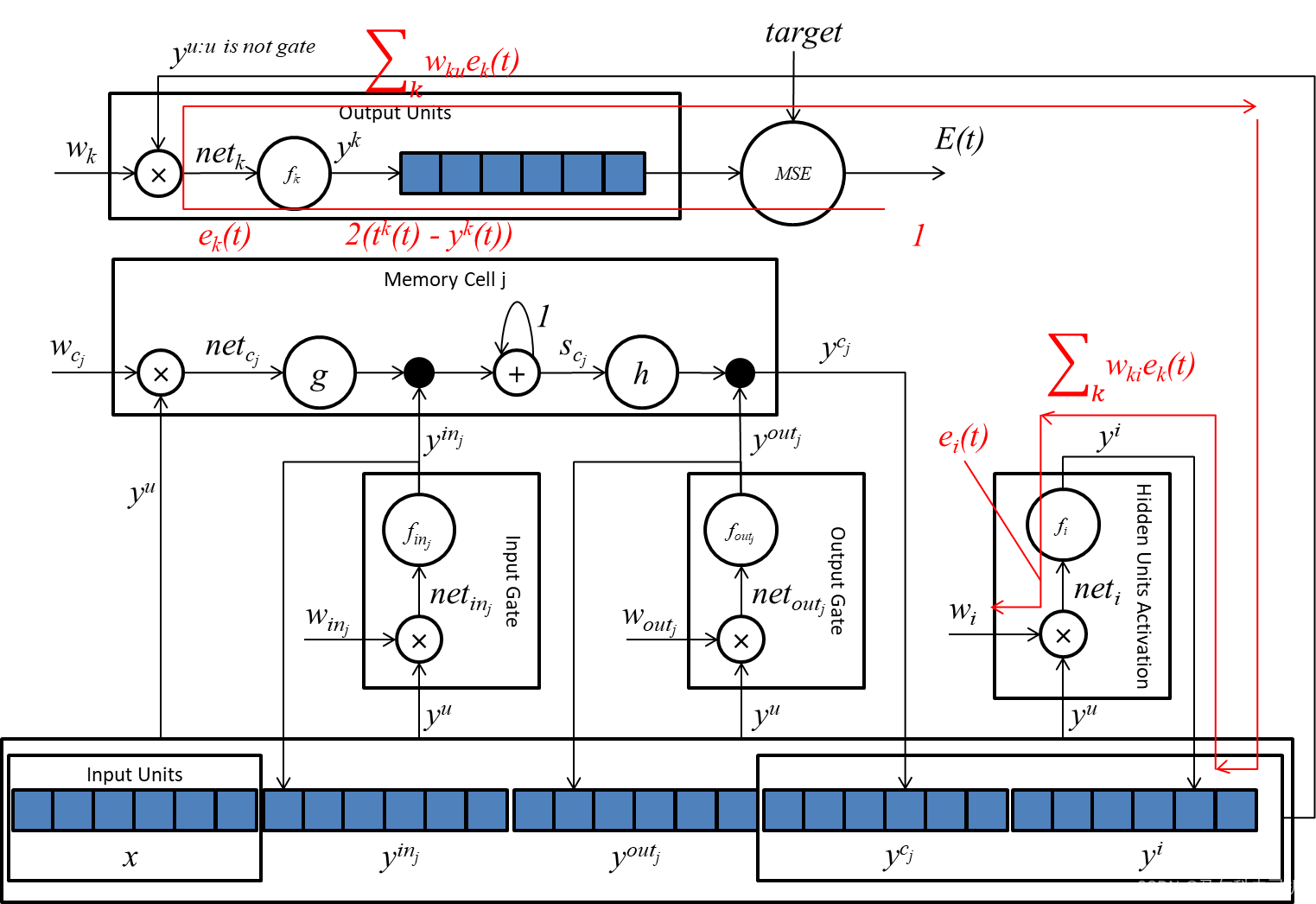
在这里插入图片描述

式20的第一个因子很好理解，就是隐藏单元的激活函数的求导。第二个因子会有点难以理解。
$\sum_{k:\ k\ output\ unit}w_{ki}e_k(t) = \frac{\partial E(t)}{\partial y^i}$
我们只需要画个神经网络的图就很好理解了：
在这里插入图片描述
根据后向传播的规则，对于一个数据节点，如果同时作为多个操作节点的输入，那么其梯度值为所有上游梯度值之和。

5.4 输出门误差计算

令 $l=out_j$ ，可得：
$\begin{aligned} e_{out_j}(t) &= - \frac{\partial E(t)}{\partial net_{out_j}(t)}\\ &= f_{out_j}'(net_{out_j}(t))(\sum_{v=1}^{s_j} h(s_{c_j^v})\sum_{k:\ k\ output\ unit}w_{kc_j^v}e_k(t))\tag{21}.\\ \end{aligned}$
上边这个式子是针对有多个记忆块(memory block)，每个记忆块 $block_v$ 都与其前边的所有记忆块 $block_x,x<v$ 相连的情况，我们为了便于理解做一个简化，只有一个包含了多个记忆单元的记忆块，因此上式可以写成：
$\begin{aligned} e_{out_j}(t) &= - \frac{\partial E(t)}{\partial net_{out_j}(t)}\\ &= f_{out_j}'(net_{out_j}(t))h(s_{c_j}(t))\sum_{k:\ k\ output\ unit}w_{kc_j}e_k(t).\\ \end{aligned}$
这个公式有三个因子：

$f_{out_j}'(net_{out_j}(t))$ ：这是输出门的激活函数的求导，
$h(s_{c_j}(t))$ ：根据向量相乘的求导公式， $\frac{\partial y^{c_j}}{\partial y^{out_j}} = h(s_{c_j}(t))$ ，
$\sum_{k:\ k\ output\ unit}w_{kc_j}e_k(t)$ ：可参考式20的解释。

我们同样可以通过梯度传播图来理解这个公式：
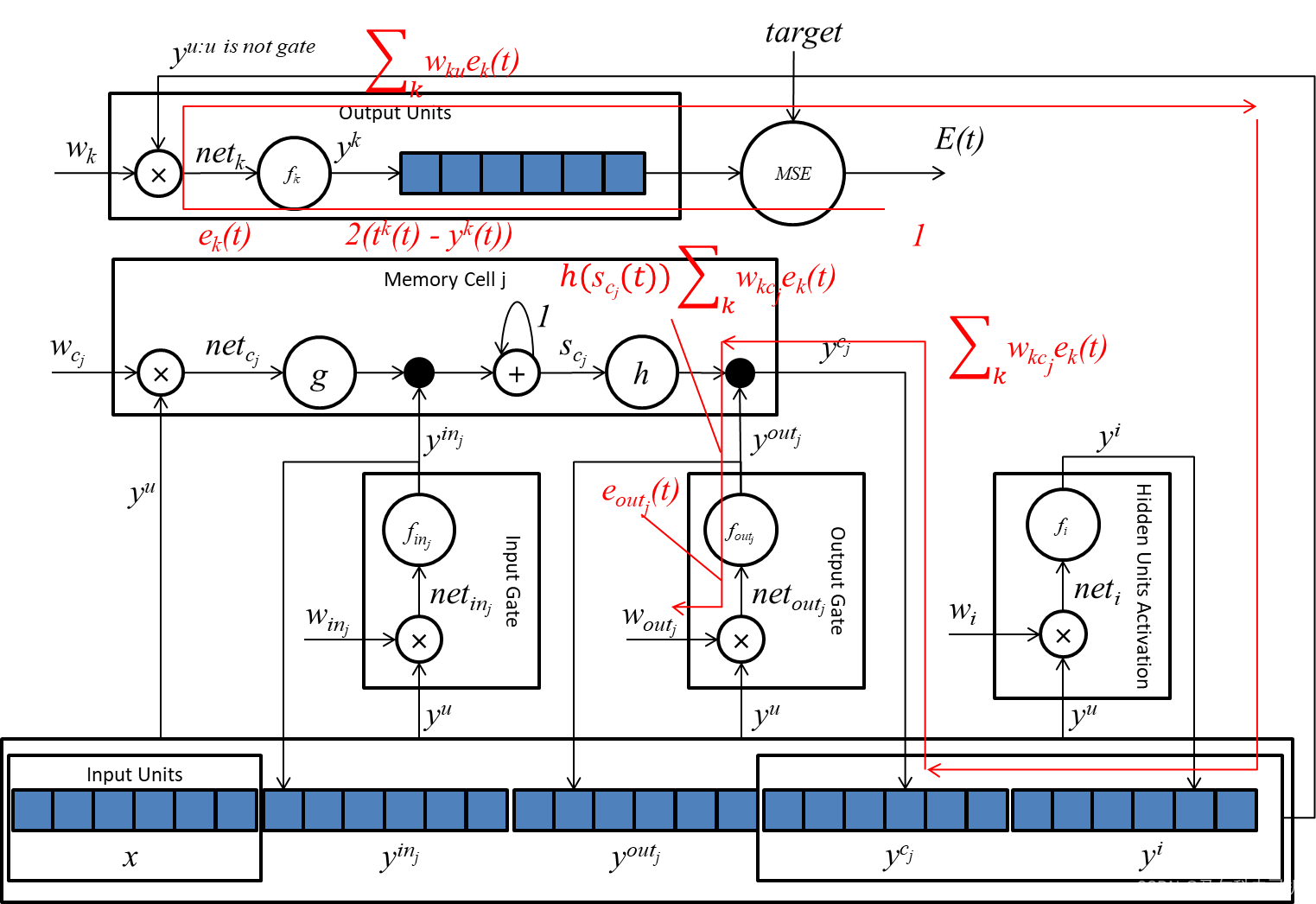
在这里插入图片描述

对于任何单元或门 $l$ ，在时间点 $t$ ，对权重 $w_{lm}$ 的贡献值为：
$\Delta w_{lm}(t) = \alpha e_l(t)y^m(t-1).\tag{22}$
式22的推导过程为：
$\begin{aligned} \Delta w_{lm}(t) &= - \alpha \frac{\partial E(t)}{\partial w_{lm}}&(式17)\\ & = \alpha(- \frac{\partial E(t)}{\partial net_l(t)}) \frac{\partial net_l(t)}{\partial w_{lm}}&(应用链式规则求导)\\ & = \alpha e_{l}(t) \frac{\partial net_l(t)}{\partial w_{lm}} &(代入式18)\\ &= \alpha e_l(t)y^m(t-1) \end{aligned}$

我们可以把前文中得到的 $e_i(t),e_{out_j}(t), e_k(t)$ 代入上式得到相应的 $\Delta w_{lm}$ 值。

5.5 输入门的误差计算

由于输入门藏得比较深，因此需要先计算一个中间节点 $s_{c_j}$ 的误差。
$\begin{aligned} e_{s_{c_j}}(t) &= - \frac{\partial E(t)}{\partial s_{c_{j}}(t)}\\ &= f_{out_j}(net_{out_j}(t))h'(s_{c_{j}}(t)) (\sum_{k:\ k\ output\ unit}w_{kc_j}e_k(t)) \tag{23} \end{aligned}$

这个式子有三个因子：

$f_{out_j}(net_{out_j}(t))$ ： $\frac{\partial y^{c_j}(t)}{\partial h(s_{c_{j}}(t))} = f_{out_j}(net_{out_j}(t))$ ，
$h'(s_{c_{j}}(t))$ ： $s_{c_j}(t)$ 后的激活函数 $h$ 的求导。
$\sum_{k:\ k\ output\ unit}w_{kc_j}e_k(t)$ ：同公式21的解释。

我们令 $l=in_j$ 或者 $l=c_j^v$ ，计算：
$-\frac{\partial E(t)}{\partial w_{lm}} = \sum_{v=1}^{s_j}e_{s_{c_j}^v}(t) \frac{\partial s_{c_j}^v(t)}{\partial w_{lm}}\tag{24}.$
同样，式24采用了多记忆块模型，我们为了便于理解先简化为单记忆块模型，上式可以简化为：
$-\frac{\partial E(t)}{\partial w_{lm}} = e_{s_{c_j}}(t) \frac{\partial s_{c_j}(t)}{\partial w_{lm}}.$
令 $l=in_j$ ，我们进一步计算上式的第二个因子 $\frac{\partial s_{c_j}(t)}{\partial w_{lm}}$ ：
我们代入 $s_{c_j}$ 的计算公式：
$s_{c_j}(t) = s_{c_j}(t-1) + g(net_{c_j}(t)) f_{in_j}(net_{in_j}(t))$
可得：
$\frac{\partial s_{c_j}(t)}{\partial w_{in_j m}} = \frac{\partial s_{c_j}(t-1)}{\partial w_{in_j m}}+ g(net_{c_j}(t))f_{in_j}'(net_{in_j}(t))y^m(t-1)\tag{25}$
题目都做到这里了，估计大家都可以理解上边这个式子怎么得到的吧。

到此我们可得在时间 $t$ ， $w_{in_j m}$ 的误差更新值为：
$\Delta w_{in_j m}(t) = \alpha \sum_{v=1}^{s_j} e_{s_{c_j}}(t) \frac{\partial s_{c_j}(t)}{\partial w_{in_j m}}\tag{26}.$
下图显示了输入门的误差传播路径：
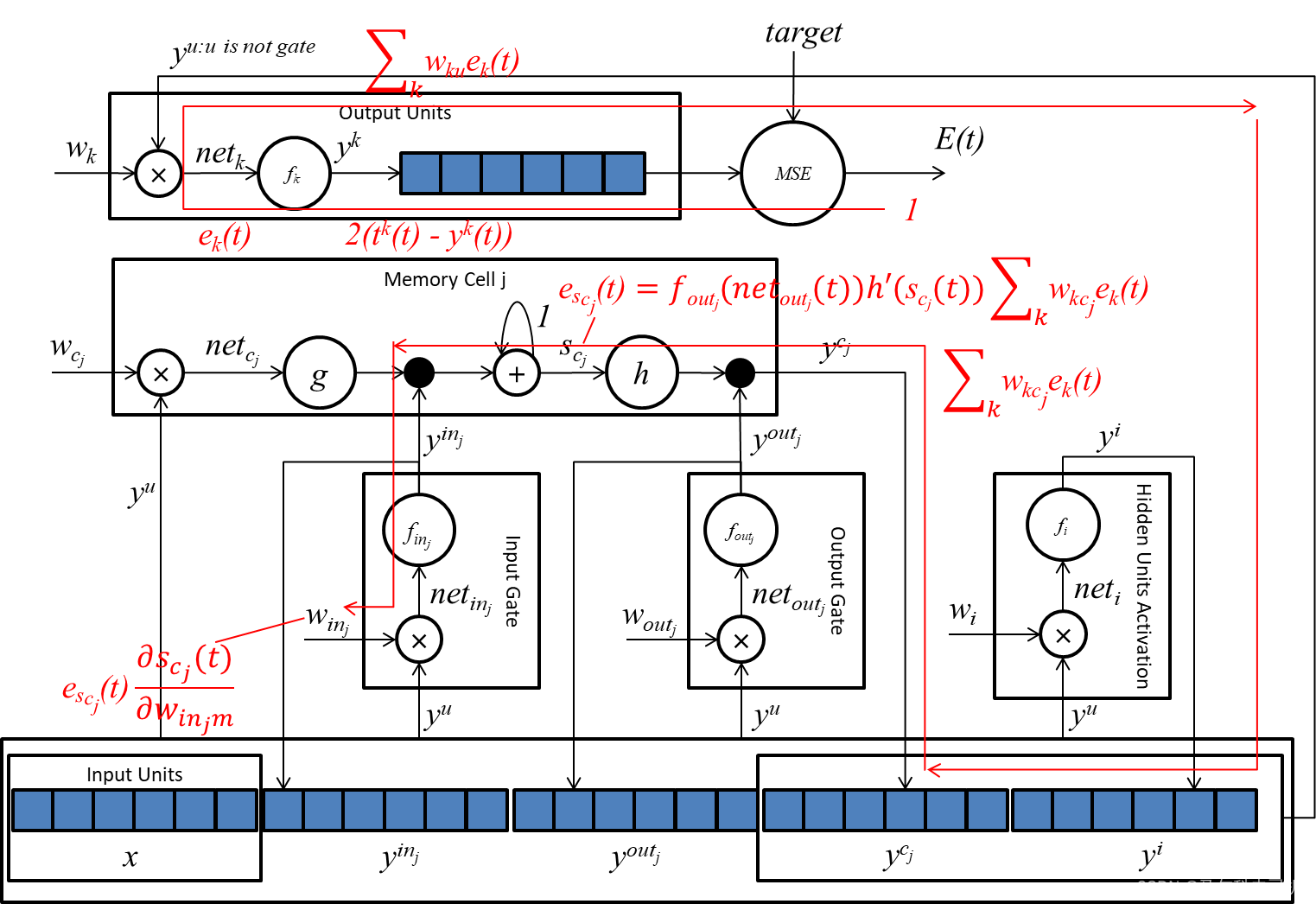
在这里插入图片描述

5.5 记忆单元的误差计算

令 $l=c_j$ ，为了计算记忆单元的误差公式，我们先计算 $\frac{\partial s_{c_j}(t)}{\partial w_{c_j} m}$ ：
代入 $s_{c_j}$ 的计算公式：
$s_{c_j}(t) = s_{c_j}(t-1) + g(net_{c_j}(t)) f_{in_j}(net_{in_j}(t))$
可得：
$\frac{\partial s_{c_j}(t)}{\partial w_{c_j} m} = \frac{\partial s_{c_j}(t-1)}{\partial w_{c_j m}} + g'(net_{c_j}(t))(f_{in_j}(net_{in_j}(t)))y^m(t-1)\tag{27}.$
上式的理解类似于式25。

因此记忆单元的权重 $w_{c_j m}$ 在 $t$ 时刻的更新值为：
$\Delta w_{c_j m} (t)=\alpha e_{s_{c_j}}(t) \frac{\partial s_{c_j}(t)}{\partial w_{c_j} m}\tag{28}.$
误差值传播路径图：
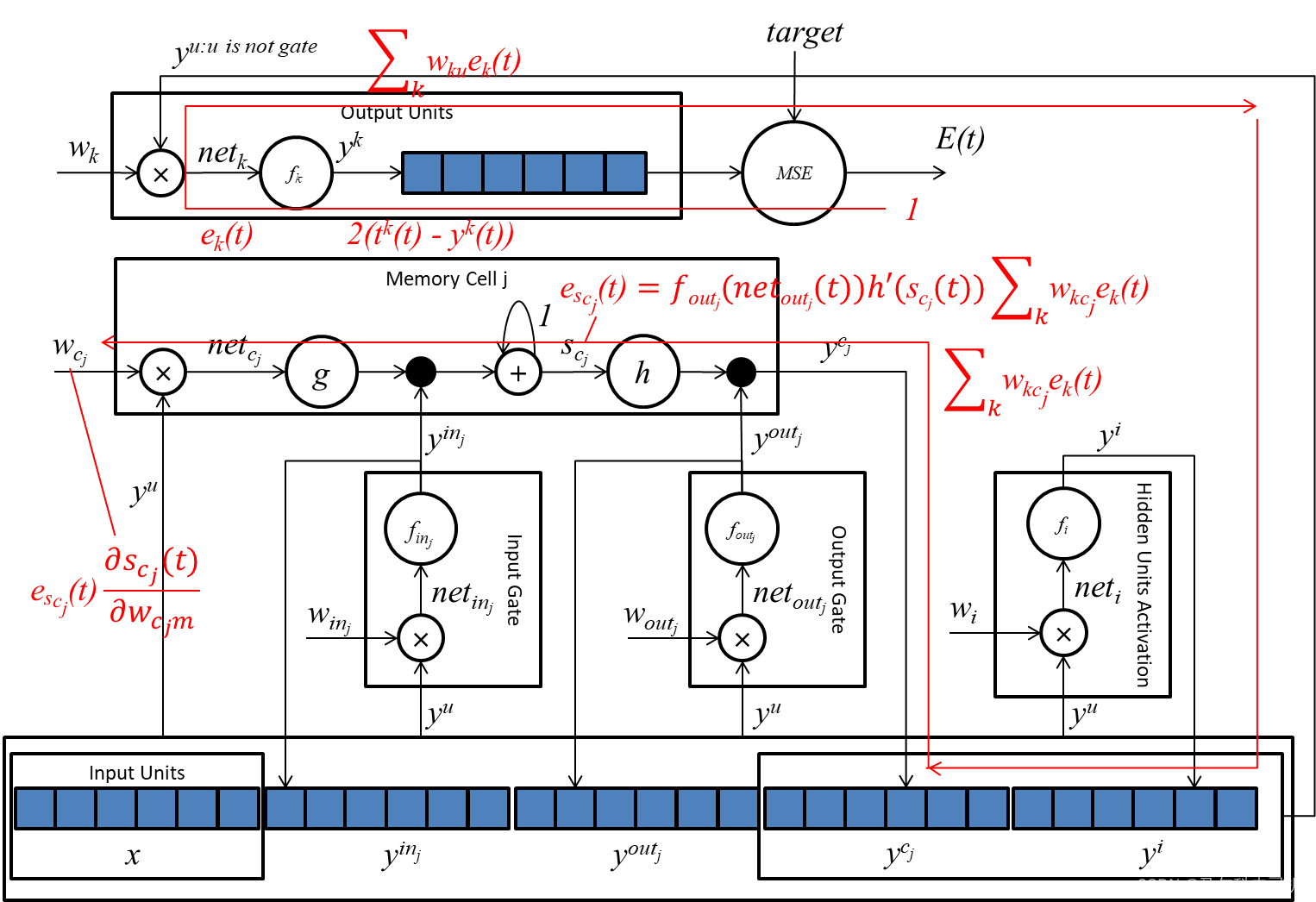
在这里插入图片描述

5.6 权重更新算法的时间复杂度

令 $K$ 为输出向量的长度， $C$ 为记忆单元块的个数（在我们简化的单记忆块的版本中，该值为1）， $S$ 为每个记忆块中记忆单元的个数， $H$ 为隐藏单元的向量长度， $I$ 为与记忆单元、门、和隐藏单元互相连接的向量度。
这个 $I$ 指的就是向量 $y^u$ 的长度，如下图所示：
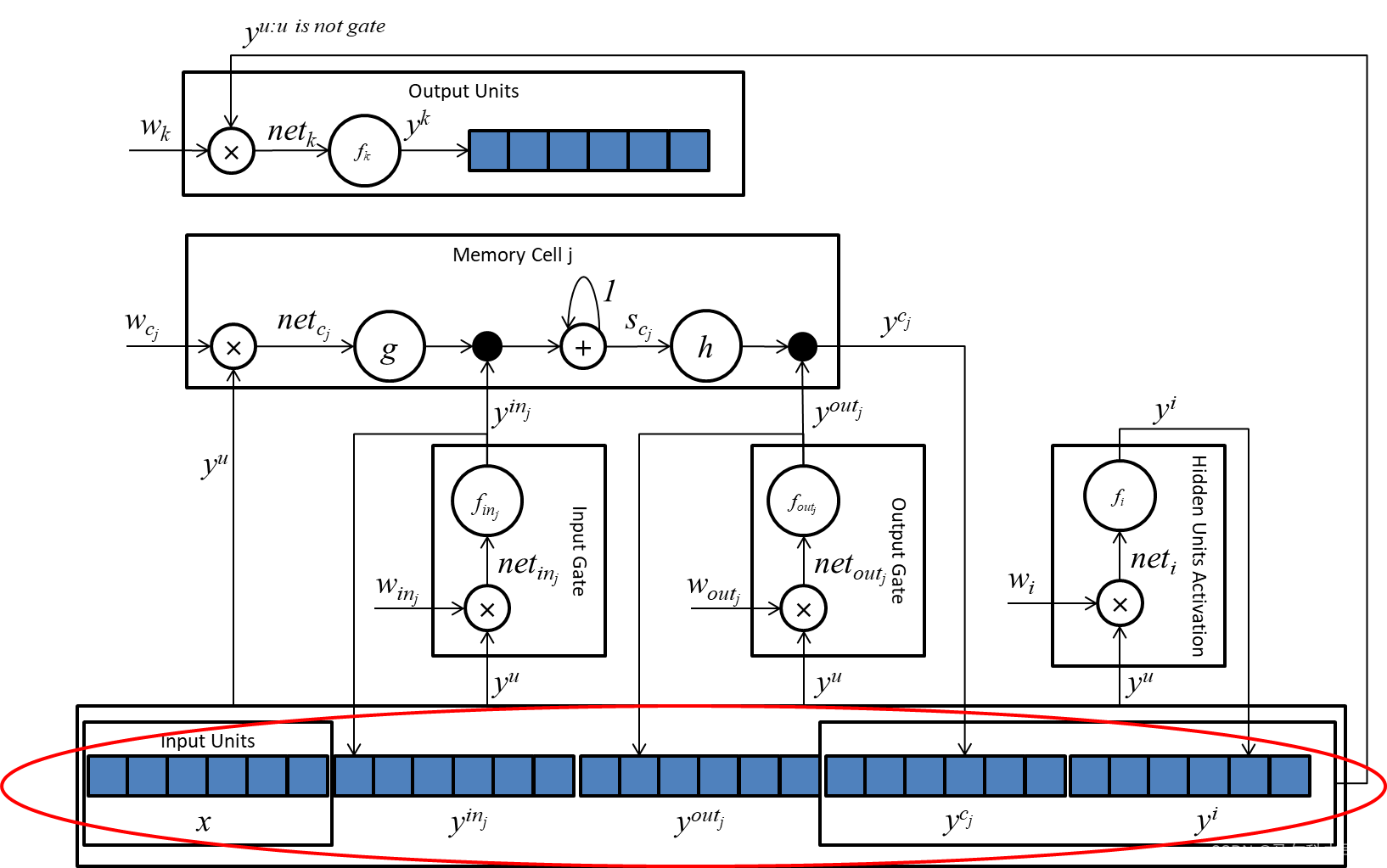
在这里插入图片描述
所有权重数据的个数为 $W$ ：
$W = KH + K CS + CS I + 2 C I + H I .$
其中：

$KH + K CS$ 为 $w_k$ 的权重个数。
$CS I$ ： $w_{c_j}$ 的权重个数。
$2 C I$ ： $w_{in_j},w_{out_j}$ 的权重个数之和。
$H I$ ： $w_i$ 的权重个数。

更新所有权重需要 $KH + K CS + CS I + 2 C I + H I$ 步操作， $O (W) = O (KH + K CS + CS I + H I)$

在程序开发过程中，我们只需要实现等式(19)，(20)，(21)，(22)，(23)，(25)，(26)，(27)，(28)。因此我们只需要逐步计算每个等式的时间复杂度即可算出整个算法的时间复杂度。

式19： $e_k(t) = f'(net_k(t))(t^k(t) - y^k(t))$ ，需要 $K$ 步计算，
式20： $e_i(t) = f_i'(net_i(t))\sum_{k:\ k\ output\ unit}w_{ki}e_k(t)$ ，需要 $KH$ 步计算，
式21： $e_{out_j}(t) = f_{out_j}'(net_{out_j}(t))(\sum_{v=1}^{s_j} h(s_{c_j^v})\sum_{k:\ k\ output\ unit}w_{kc_j^v}e_k(t))$ ，需要 $K CS$ 步计算，
式22： $\Delta w_{lm}(t) = \alpha e_l(t)y^m(t-1)$ ，当 $l = k$ 时需要 $K (H + C)$ 步计算，当 $l = i$ 时需要 $H I$ 步计算，当 $l=out_j$ 时需要 $C I$ 步计算，
式23： $e_{s_{c_j}}(t) = f_{out_j}(net_{out_j}(t))h'(s_{c_{j}}(t)) (\sum_{k:\ k\ output\ unit}w_{kc_j}e_k(t))$ ，需要 $K CS$ 步计算，
式25： $\frac{\partial s_{c_j}(t)}{\partial w_{in_j m}} = \frac{\partial s_{c_j}(t-1)}{\partial w_{in_j m}}+ g(net_{c_j}(t))f_{in_j}'(net_{in_j}(t))y^m(t-1)$ ，需要 $CS I$ 步计算，
式26： $\Delta w_{in_j m}(t) = \alpha \sum_{v=1}^{s_j} e_{s_{c_j}}(t) \frac{\partial s_{c_j}(t)}{\partial w_{in_j m}}$ ，需要 $CS I$ 步计算，
式27： $\frac{\partial s_{c_j}(t)}{\partial w_{c_j} m} = \frac{\partial s_{c_j}(t-1)}{\partial w_{c_j m}} + g'(net_{c_j}(t))(f_{in_j}(net_{in_j}(t)))y^m(t-1)$ ，需要 $CS I$ 步计算，
式28： $\Delta w_{c_j m} (t)=\alpha e_{s_{c_j}}(t) \frac{\partial s_{c_j}(t)}{\partial w_{c_j} m}$ ，需要 $CS I$ 步计算。