文章目录
- 题目
- 标题和出处
- 难度
- 题目描述
- 要求
- 示例
- 数据范围
- 解法一
- 思路和算法
- 代码
- 复杂度分析
- 解法二
- 思路和算法
- 代码
- 复杂度分析
题目
标题和出处
标题:二叉树的最近公共祖先
出处:236. 二叉树的最近公共祖先
难度
5 级
题目描述
要求
给定一个二叉树,找到该树中两个指定结点的最近公共祖先。
最近公共祖先的定义为:两个结点 p \texttt{p} p 和 q \texttt{q} q 的最近公共祖先是满足 p \texttt{p} p 和 q \texttt{q} q 都是其后代的最低的结点 T \texttt{T} T(一个结点也可以是它自己的祖先)。
示例
示例 1:
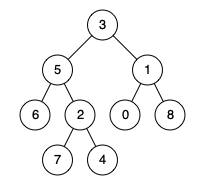
输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1 \texttt{root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1} root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
输出: 3 \texttt{3} 3
解释:结点 5 \texttt{5} 5 和结点 1 \texttt{1} 1 的最近公共祖先是结点 3 \texttt{3} 3。
示例 2:
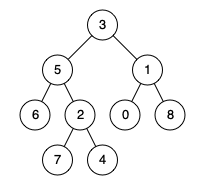
输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4 \texttt{root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4} root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
输出: 5 \texttt{5} 5
解释:结点 5 \texttt{5} 5 和结点 4 \texttt{4} 4 的最近公共祖先是结点 5 \texttt{5} 5。因为根据定义最近公共祖先结点可以为结点本身。
示例 3:
输入: root = [1,2], p = 1, q = 2 \texttt{root = [1,2], p = 1, q = 2} root = [1,2], p = 1, q = 2
输出: 1 \texttt{1} 1
数据范围
- 树中结点数目在范围 [2, 10 5 ] \texttt{[2, 10}^\texttt{5}\texttt{]} [2, 105] 内
- -10 9 ≤ Node.val ≤ 10 9 \texttt{-10}^\texttt{9} \le \texttt{Node.val} \le \texttt{10}^\texttt{9} -109≤Node.val≤109
- 所有 Node.val \texttt{Node.val} Node.val 各不相同
- p ≠ q \texttt{p} \ne \texttt{q} p=q
- p \texttt{p} p 和 q \texttt{q} q 均存在于给定的二叉树中
解法一
思路和算法
二叉树中的每个结点对应一条从根结点到该结点的路径。对于结点 p p p 和 q q q,其对应的路径一定存在重合部分,重合部分的结点都是 p p p 和 q q q 的公共祖先,其中深度最大的公共祖先即为最近公共祖先。
考虑示例 1 和示例 2 使用的二叉树。

示例 1 中, p = 5 p = 5 p=5, q = 1 q = 1 q=1。结点 5 5 5 对应的路径是 [ 3 , 5 ] [3, 5] [3,5],结点 1 1 1 对应的路径是 [ 3 , 1 ] [3, 1] [3,1],唯一的公共祖先是 3 3 3,最近公共祖先是 3 3 3。
示例 2 中, p = 5 p = 5 p=5, q = 4 q = 4 q=4。结点 5 5 5 对应的路径是 [ 3 , 5 ] [3, 5] [3,5],结点 4 4 4 对应的路径是 [ 3 , 5 , 2 , 4 ] [3, 5, 2, 4] [3,5,2,4],公共祖先是 3 3 3 和 5 5 5,最近公共祖先是 5 5 5。
当遍历到一个结点时,即可得到从根结点到该结点的路径,将路径反转之后即可得到从该结点到根结点的路径。对于结点 p p p 和 q q q 分别得到从当前结点到根结点的路径,两条路径相交处的结点即为最近公共祖先。
为了得到反向路径,需要使用哈希表存储每个结点的父结点。对二叉树深度优先搜索,在遍历过程中将每个结点的父结点存入哈希表。遍历结束之后,从结点 p p p 出发,每次移动到当前结点的父结点,直到到达根结点时,即得到从结点 p p p 到根结点的路径。在寻找从结点 p p p 到根结点的路径的过程中,使用哈希集合存储访问过的结点。然后从结点 q q q 出发,每次移动到当前结点的父结点,寻找从结点 q q q 到根结点的路径,第一个遇到的在哈希集合中的结点即为最近公共祖先。
代码
class Solution {Map<TreeNode, TreeNode> parentMap = new HashMap<TreeNode, TreeNode>();Set<TreeNode> visited = new HashSet<TreeNode>();public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {dfs(root);TreeNode node = p;while (node != null) {visited.add(node);node = parentMap.get(node);}TreeNode ancestor = q;while (!visited.contains(ancestor)) {ancestor = parentMap.get(ancestor);}return ancestor;}public void dfs(TreeNode node) {TreeNode left = node.left, right = node.right;if (left != null) {parentMap.put(left, node);dfs(left);}if (right != null) {parentMap.put(right, node);dfs(right);}}
}
复杂度分析
-
时间复杂度: O ( n ) O(n) O(n),其中 n n n 是二叉树的结点数。深度优先搜索访问每个结点一次,需要 O ( n ) O(n) O(n) 的时间,对于结点 p p p 和结点 q q q,寻找从当前结点到根结点的路径的时间不超过 O ( n ) O(n) O(n),因此总时间复杂度是 O ( n ) O(n) O(n)。
-
空间复杂度: O ( n ) O(n) O(n),其中 n n n 是二叉树的结点数。空间复杂度主要是哈希表、哈希集合和栈的空间,哈希表需要 O ( n ) O(n) O(n) 的空间存储每个结点的父结点,哈希集合和栈的空间取决于二叉树的高度,二叉树的高度不超过 O ( n ) O(n) O(n),因此总空间复杂度是 O ( n ) O(n) O(n)。
解法二
思路和算法
考虑二叉树中的每个结点,可能有以下情况。
-
如果 p p p 和 q q q 中的一个结点是当前结点,另一个结点在以当前结点为根结点的子树中,则当前结点即为 p p p 和 q q q 的最近公共祖先。
-
如果 p p p 和 q q q 分别位于当前结点的左子树和右子树中,则当前结点即为 p p p 和 q q q 的最近公共祖先。
-
如果 p p p 和 q q q 位于当前结点的同一个子树中,则 p p p 和 q q q 的最近公共祖先位于当前结点的同一个子树中。
上述情况中的情况 1 和情况 2 为当前结点是 p p p 和 q q q 的最近公共祖先,对于情况 3,需要在子树中继续寻找 p p p 和 q q q 的最近公共祖先,最近公共祖先一定满足情况 1 或情况 2。因此,最近公共祖先可能的情况一共有两种。
为了寻找最近公共祖先,需要从根结点开始深度优先搜索。对于每个结点,在当前子树中寻找 p p p 和 q q q 是否存在,如果 p p p 和 q q q 都存在则返回最近公共祖先,如果 p p p 和 q q q 只存在一个则返回存在的结点。以下将 p p p 和 q q q 统称为「目标结点」。
具体做法如下。
-
如果当前结点为 p p p 或 q q q,则返回当前结点。
-
否则,在当前结点的左子树和右子树中分别寻找 p p p 和 q q q。
-
如果两个子树中都存在目标结点,则 p p p 和 q q q 分别在两个子树中,当前结点即为最近公共祖先。
-
如果只有一个子树中存在目标结点,则在该子树中寻找最近公共祖先。
-
上述过程是一个递归的过程,递归的终止条件是当前结点为 p p p 或 q q q,其余情况则调用递归。
对于每个结点,首先访问其子结点寻找目标结点和公共祖先,然后根据访问子结点的结果得到当前结点的结果。计算结果的顺序是先计算子结点的结果,后计算当前结点的结果,该顺序实质是后序遍历。由于在计算每个结点的结果时,该结点的子结点的结果已知,该结点的结果由子结点的结果决定,因此可以确保结果正确。
代码
class Solution {public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {if (root == p || root == q) {return root;}TreeNode leftAncestor = null, rightAncestor = null;if (root.left != null) {leftAncestor = lowestCommonAncestor(root.left, p, q);}if (root.right != null) {rightAncestor = lowestCommonAncestor(root.right, p, q);}if (leftAncestor != null && rightAncestor != null) {return root;}return leftAncestor != null ? leftAncestor : rightAncestor;}
}
复杂度分析
-
时间复杂度: O ( n ) O(n) O(n),其中 n n n 是二叉树的结点数。每个结点都被访问一次。
-
空间复杂度: O ( n ) O(n) O(n),其中 n n n 是二叉树的结点数。空间复杂度主要是递归调用的栈空间,取决于二叉树的高度,最坏情况下二叉树的高度是 O ( n ) O(n) O(n)。

-核心PPT资料下载)



)






,以及写一个日志模板)






