目录
题目信息
题目分析:
法一:
遍历二维数组(低效)
思路
源码
局限性
法二:
对每一行二分查找(有所提效)
思路
源码
局限性
法三:
利用一切有利条件使用二分查找
思路
源码
局限性
二分查找源码:
题目信息
有一个数字矩阵,矩阵的每行从左到右是递增的,矩阵从上到下是递增的,请编写程序在这样的矩阵中查找某个数字是否存在。
要求:时间复杂度小于O(N);
题目分析:
这道题是什么情况呢?其实就是说,有下面的这样一个满足要求的矩阵:

干脆 , 更直观一点:
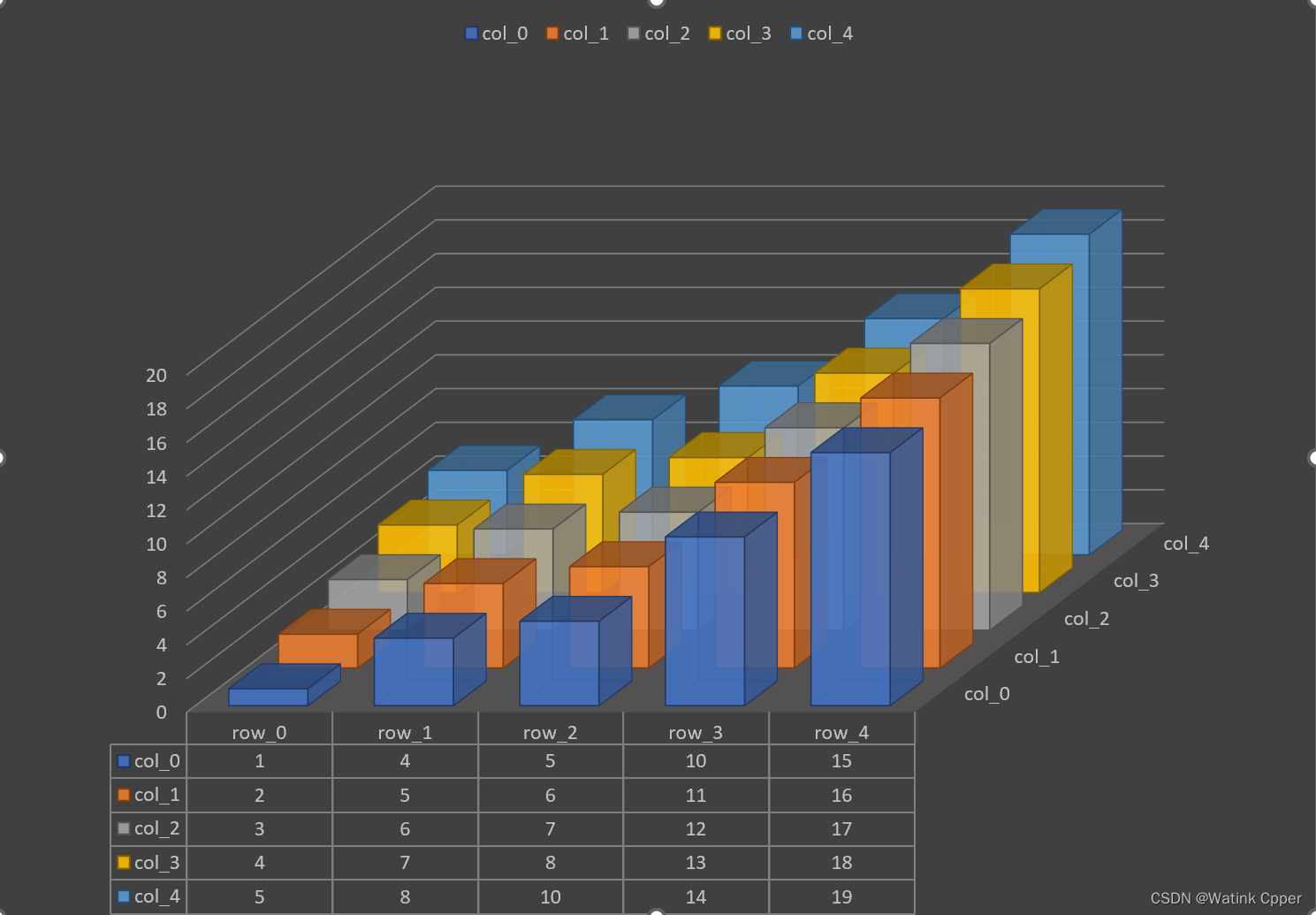
也就是,在这样的矩阵(每一行从左到右递增,每一列从上到下递增)中查找一个特定的元素。
如果找到,确定它的位置;如果找不到,输出 -1 ;
法一:
遍历二维数组(低效)
思路
我们首先最容易想到的,也是最简单的方法,就是遍历数组,一个一个去试一试,看看能不能找到。
源码
#define ROW 5
#define COL 5int main()
{int key;scanf("%d",&key);char arr[ROW][COL] = {{1,2,3,4,5},{4,5,6,7,8},{5,6,7,8,10},{10,11,12,13,14},{15,16,17,18,19}};int i = 0;for(i = 0;i < ROW;i++){int j = 0;for(j = 0;j < COL;j++){if(key ==arr[i][j]){printf("找到了,在%d行%d列\n",i,j);break;}}}return 0;
}
对照一下结果,代码是正确的。
局限性
经过计算,遍历算法的时间复杂度为O(N^2)
虽然遍历算法思路简单易想,这样的时间复杂度太大,不再符合题目要求。
法二:
对每一行二分查找(有所提效)
思路
由于数组的每一行都是有序的,这样就满足了二分查找的使用条件,所以可以直接对每一行二分查找:
直观一点:
源码
#define ROW 5
#define COL 5
#include<stdio.h>
#include<string.h>
int bi_search(int arr[ROW],int sz,int key)
{int f = 0;int left = 0;int right = sz-1;int mid = (left + right)/2;while(left<=right){ mid = (left + right)/2;if(arr[mid] > key){right = mid - 1;}else if(arr[mid] < key){left = mid + 1;}else if(arr[mid] == key){f = 1;return mid;}}if(f == 0){return -1;}
}
int main()
{int key;scanf("%d",&key);int arr[ROW][COL] = {{1,2,3,4,5},{4,5,6,7,8},{5,6,7,8,10},{10,11,12,13,14},{15,16,17,18,19}};int i = 0;int f = 0;for(i = 0;i < ROW;i++){int ret = bi_search(arr[i],COL,key);if(ret != -1){f = 1;printf("找到了,在%d行%d列\n",i,ret);}}if(f == 0){printf("找不到");}return 0;
}
在实际动手写代码时,我也遇到了一些问题,比如刚开始把打印找不到放在循环内,结果出现了这样的结果:
这就挺尴尬的,解决办法是引入判断变量f,然后先假设找不到f初始化为0;如果找到,f置为1,如果直到循环完毕,f都没有被置为1,则就是整个数组都没有key;
局限性
经计算,对每一行进行二分查找算法的时间复杂度为O(N log2(N))
虽然速度有所提升,但是效率仍然达不到题目要求。
法三:
利用一切有利条件使用二分查找
思路
我们可以先对行进行二分查找
假设找9,在比9大的前一个元素前停下,由于行列都是从小到大递增的,所以可以断定后两行没有要找的元素9
对行二分查找
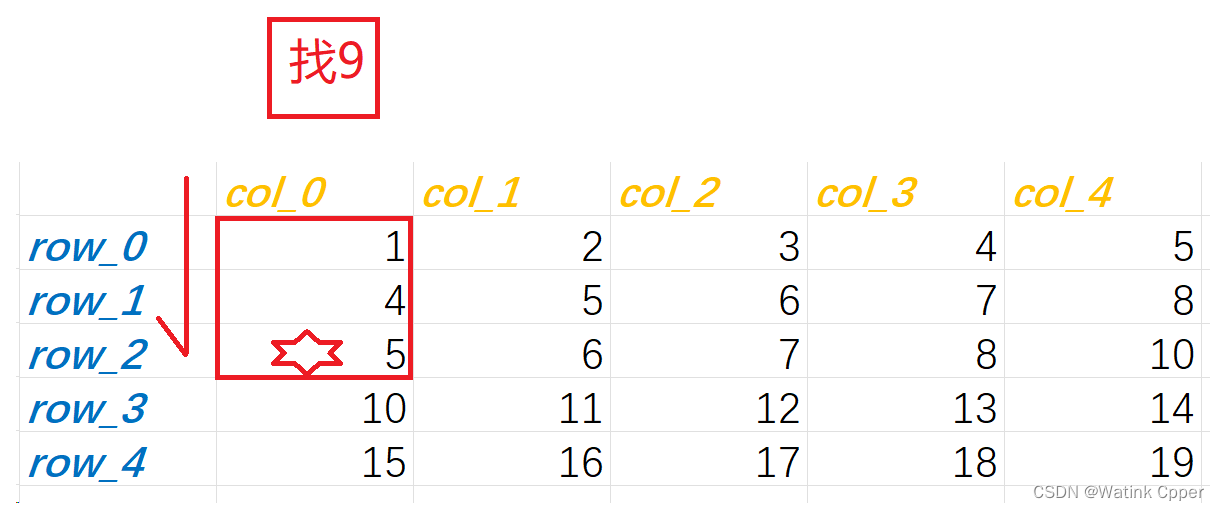
后两行没有9
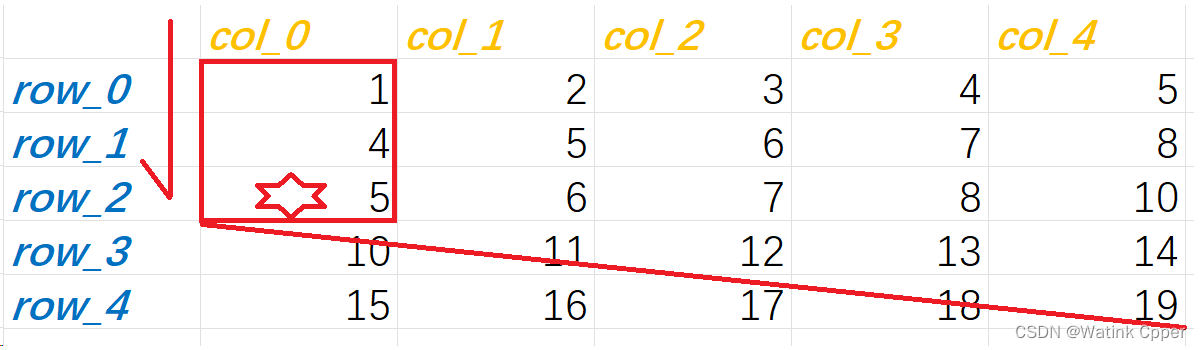
接下来对行进行二分查找,但是我们发现所有的行都小于要查找的key,所以接下来只能对剩下的3行分别二分查找。

在这种n = 5 ,的情况下,我们发现时间复杂度并没有降低多少,我们分析一下:
每一行二分,需要5次;
而先列,进行排除;再行,需要4次;
但是在一般情况下,n可能很大,可能是100000,甚至更大,在这种情况下,程序有很大程度的提效。

时间复杂度N的趋势:
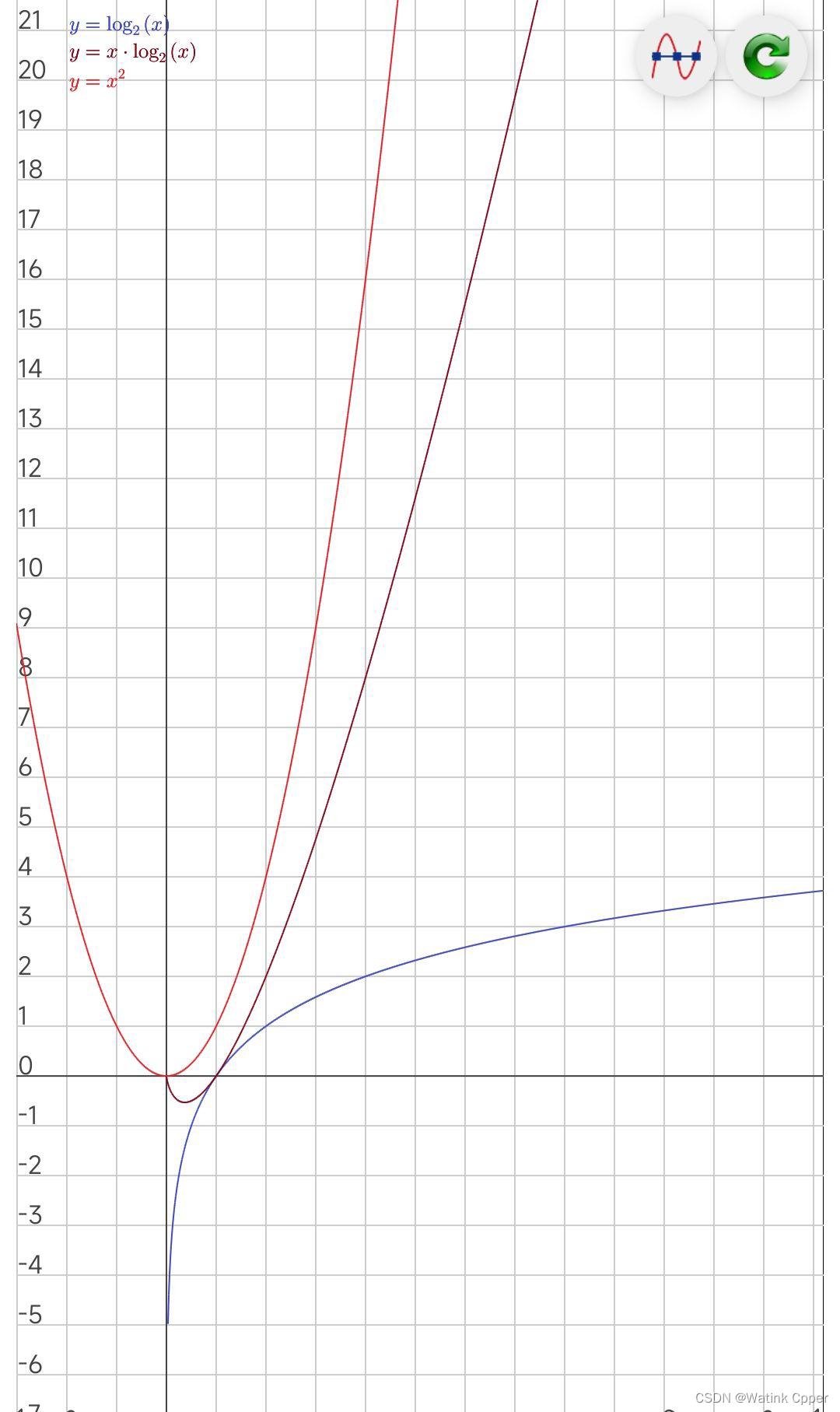
源码
我在写这个代码的时候遇到了一些问题,在对第一列进行二分查找后,在不再次遍历数组的情况下(不再增加时间复杂度),没有办法定位到合适的位置(在这个位置上,数组的后一个元素的大小大于key,数组前一个元素大小小于key,),你可以想一想,私信我交流。
局限性
假设第k个找到合适位置,需要进行两次二分查找,时间复杂度是(log2(N)),剩下每一行都可能会出现key;
但在此处,我选择对排除后的每一行进行二分查找,时间复杂度为(k*log2(k));
则时间复杂度的表达式为:
T = log2(N)+ k*log2(k) (k < N)
最差情况,k == N,时间复杂度O(N* ( log2 (N) ) );
最优解:k == 0,时间复杂度O(1);
其实,我们可以设计更复杂的算法,这样可以进一步提高效率;
提供一种思路:沿着对角线遍历n*n的矩阵,找到合适的停留点,这样又可以排除一部分可能:
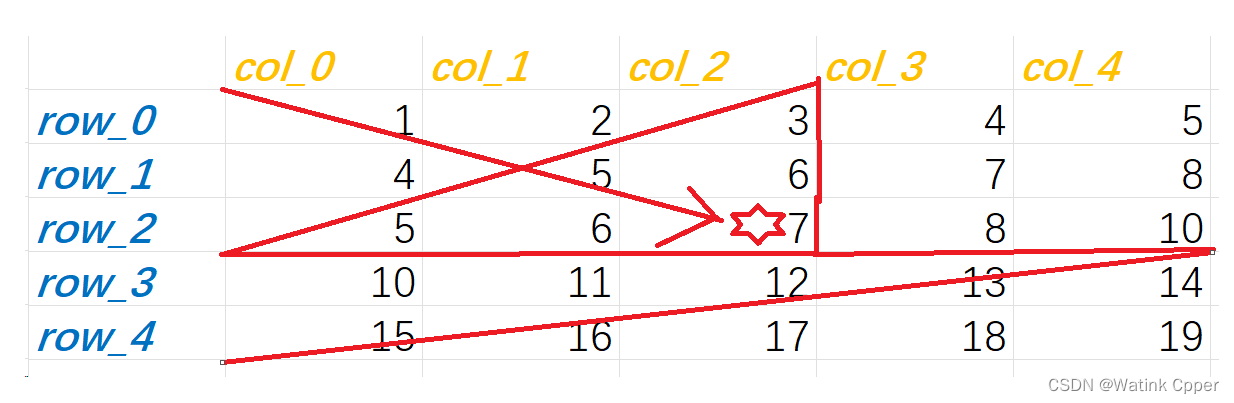
如果你可以巧妙利用题目信息,那么,即使有时间限制,oj题目对你来说一定不在话下!
加油吧!
二分查找源码:
int bi_search(int arr[ROW],int sz,int key)//参数分别是:要查找的行,数组元素的个数,要查找的对象
{int f = 0;int left = 0;int right = sz-1;int mid = (left + right)/2;while(left<=right){ mid = (left + right)/2;if(arr[mid] > key){right = mid - 1;}else if(arr[mid] < key){left = mid + 1;}else if(arr[mid] == key){f = 1;return 1;//如果找到,返回1}}if(f == 0){return -1;//如果找不到,返回-1}
}
完~
未经作者同意禁止转载



)
)










)




