每日一句：你的日积月累终会成为别人的望尘莫及
目录
常数时间的操作
选择排列
冒泡排列
【异或运算】
面试题：
1）在一个整形数组中，已知只有一种数出现了奇数次，其他的所有数都出现了偶数次，怎么找到出现了奇数次的数？（要求时间复杂度O(N),空间复杂度O（1））
2）在一个整形数组中，已知有两种数出现了奇数次，其他的所有数都出现了偶数次，怎么找到这两种数？（要求时间复杂度O(N),空间复杂度O（1））
插入排序
二分法的详解与扩展
1）在一个有序数组中，找某个数是否存在
2）在一个有序数组中，找大于等于某个数最左侧的位置
局部最小值问题
在一个数组中arr无序，且任何两个相邻的数不相等，求局部最小
对数器的概念和使用
递归行为和递归行为时间复杂度的估算
归并排序
小和问题
在一个数组中，每一个数左边比当前数小的数累加起来，叫做这个数组的小和。求一个数组的小和。
例：[1,2,4,3,5]，1左边比1小的数没有；2左边比2小的数，1；4左边比4小的数，1,2；3左边比3小的数，1,2；5左边比5小的数1,2,4,3；
所以小和为1+1+2+1+2+1+2+4+3=17
荷兰国旗问题
问题一
给定一个数组arr,和一个数num，请把小于等于num的数放在数组的左边，大于num的数放在数组的右边.要求额外空间复杂度O（1），时间复杂度O（N）
问题二
给定一个数组arr和一个数num请把小于num的数放在数组的左边，等于num的数放在数组的中间，大于num的数放在数组的右边.要求额外空间复杂度O（1），时间复杂度O（N）.
不改进的快速排序
堆
heapinsert过程
heapify过程
堆排序
已知一个几乎有序的数组，几乎有序是指[如果把数组排好顺序的话，每个元素移动的距离可以不超过K，并且k相对于数组来说比较小]请选择一个合适的排序算法针对这个数据进行排序。
比较器的使用
桶排序思想下的排序
排序算法的稳定性及其汇总
常数时间的操作
一个操作如果和样本的数据量没有关系，每次都是固定时间内完成的操作，叫做常数操作
时间复杂度为一个算法流程中，常数操作数量的一个指标。
常用O(读作bigO)来表示。具体来说，先要对一个算法流程非常熟悉，然后去写出这个算法流程中，发生了多少常数操作，进而总结出常数操作数量的表达式。
在表达式中，只要高阶项，不要低阶项的系数，剩下的部分如果为f(N),那么时间复杂度为O（f(N)）
评价一个算法流程的好坏，先看时间复杂度的指标，然后再分析不同数据样本下的实际运行时间，也就是“常数项时间”
数组、+、-、*、/、位运算是常数操作
链表不是常数操作
额外空间复杂度
指这个流程需要多少额外空间才能支持计算下来
———————————————————————————————————————
选择排列
冒泡排列
相邻比较，谁大谁往右移
【异或运算】
1）0^N=N N^N=0
2) 满足交换、结合律
a^b=b^a (a^b)^c=a^(b^c)
（抖机灵法：不用额外分配一块内存空间）
int a=甲 int b=乙
a=a^b; ——>a=甲^乙 b=乙；
b=a^b; ——>a=甲^乙 b=甲^乙^乙=甲^0=甲；
a=a^b; ——>a=甲^乙^甲=乙^0=乙 b=甲；
前提：a和b在内存里是两块独立的区域，i位置不能等于j位置，否则会异或成0
面试题：
1）在一个整形数组中，已知只有一种数出现了奇数次，其他的所有数都出现了偶数次，怎么找到出现了奇数次的数？（要求时间复杂度O(N),空间复杂度O（1））
———————————————————————————————————————
2）在一个整形数组中，已知有两种数出现了奇数次，其他的所有数都出现了偶数次，怎么找到这两种数？（要求时间复杂度O(N),空间复杂度O（1））
- 先让eor从头异或到尾，结尾时eor=a^b≠0
- a和b一定有一位不一样的，假设第8位因为把整个数组分成2类；第1类：第8位是0；第2类：第8位是1
eor1只异或第8位是1的数；eor1为a或b
3.eor^eor1为另一个a或b
把一个不为0的数最右侧的1，提取出来的操作：int rightone=eor&(~eor+1);
插入排序
时间复杂度O(
),额外空间复杂度O(1)
算法流程按照最差情况来估计时间复杂度
数据状况不同会导致算法流程的时间复杂度不一样
选择排序和冒泡排序算法和数据状况无关
二分法的详解与扩展
1）在一个有序数组中，找某个数是否存在
-
2）在一个有序数组中，找大于等于某个数最左侧的位置
局部最小值问题
在一个数组中arr无序，且任何两个相邻的数不相等，求局部最小
优化方向1）数据状况2）问题标准
对数器的概念和使用
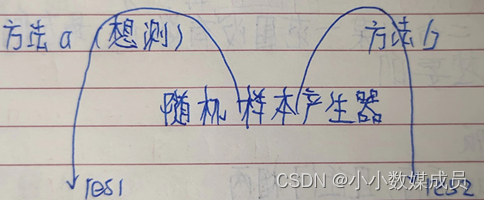
- 有一个你想要测的方法a
- 实现复杂度不好但是容易实现的方法b
- 实现一个随机样本产生器
- 把方法a和方法b跑相同的随机样本，看得到的结果是否一样
- 如果有一个随机样本使得比对结果不一致，打印样本进行人工干预，改对方法a或者方法b
- 当样本数量很多时对比测试依然正确，可以确定方法a已经正确
递归行为和递归行为时间复杂度的估算
用递归方法找一个数组中的最大值，系统上到底怎么做的？
Master公式的使用
T(N)=a*T(Nb
)+O(
)
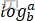>d 复杂度为O(
)
=d 复杂度为O(
)
<d 复杂度为O(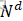
)
中点：mid=L+
=L+(R-L)>>1
归并排序
- 整体就是一个简单递归，左边排好序，右边排好序，让其整体有序
- 让其整体有序的过程用了外排序方法
- 利用master公式来求解时间复杂度
- 归并排序的实质
时间复杂度O（
）,额外空间复杂度O（N）
选择、冒泡、插入O（
）浪费了大量的比较行为
归并排序比较行为没有被浪费
比较行为被留下来了，变成了一个整体有序的部分，信息往下传递
—————————————————————————————————————
归并排序的扩展
小和问题
在一个数组中，每一个数左边比当前数小的数累加起来，叫做这个数组的小和。求一个数组的小和。
例：[1,2,4,3,5]，1左边比1小的数没有；2左边比2小的数，1；4左边比4小的数，1,2；3左边比3小的数，1,2；5左边比5小的数1,2,4,3；
所以小和为1+1+2+1+2+1+2+4+3=17
逆序对问题
在一个数组中，左边的数如果比右边的数大，则这两个数构成一个逆序对，请打印所有逆序对。
例如：数组[3,2,4,5,0],存在逆序对[3,2]、[3,0]、[2,0]、[4,0]、[5,0]
—————————————————————————————————————
荷兰国旗问题
问题一
给定一个数组arr,和一个数num，请把小于等于num的数放在数组的左边，大于num的数放在数组的右边.要求额外空间复杂度O（1），时间复杂度O（N）
问题二
给定一个数组arr和一个数num请把小于num的数放在数组的左边，等于num的数放在数组的中间，大于num的数放在数组的右边.要求额外空间复杂度O（1），时间复杂度O（N）.
—————————————————————————————————————
不改进的快速排序
1）把数组范围中的最后一个数作为划分值，然后把数组通过荷兰国旗问题分成三个部分
左侧<划分值、中间==划分值、右侧>划分值
2）对左侧范围和右侧范围，递归执行
分析：
- 划分值越靠近两侧，复杂度越高；划分值越靠近中间，复杂度越低
- 可以轻而易举的举出最差的例子，所以不改进的快速排序时间复杂度为O（
）
快排额外空间复杂度O（
）
堆
- 堆结构就是用数组实现的完全二叉树结构
- 完全二叉树中如果每棵子树的最大值都在顶部就是大根堆
- 完全二叉树中如果每棵子树的最小值都在顶部就是小根堆
- 堆结构的heapInsert（一路往上走）与heapify（一路往下走）操作
- 堆结构的增大和减少
- 优先级队列结构就是堆结构
heapinsert过程
heapify过程
堆排序
1.先让整个数组都变成大根堆结构，建立堆的过程；
- )从上到下的方法，时间复杂度O（N
）
- 从下到上的方法，时间复杂度O(N)
2．把堆的最大值和堆末尾的值交换，然后减少堆的大小，之后，再去调整堆，一直周而复始，时间复杂度O（N
）
3. 堆的大小减小成0之后，排序完成
堆排序扩展题目
已知一个几乎有序的数组，几乎有序是指[如果把数组排好顺序的话，每个元素移动的距离可以不超过K，并且k相对于数组来说比较小]请选择一个合适的排序算法针对这个数据进行排序。
小根堆在Java中优先级队列意思
PriorityQueue<Integer> heap=new PriorityQueue<>();
1.扩容怎么办？
扩容次数O（
）水平
每次扩容O（N）水平
整体O（
）水平
单位平均下来O（
）水平
2.系统写好的堆，不支持已经实现了的堆用很轻的代价，使某一结构变值，调整自己写的堆
比较器的使用
- 比较器的实质就是重载比较运算符
- 比较器可以很好的应用在特殊标准的排序上
- 比较器可以很好的应用在根据特殊标准排序的结构上
———————————————————————————————————————
不基于比较的排序都是根据数据状况做的排序
桶排序思想下的排序
- 计数排序
- 基数排序
分析
- 桶排序思想下的排序都是不基于比较的排序
- 时间复杂度O（N），额外空间复杂度O（N）
- 应用范围有限，需要样本的数据状况满足桶的划分
排序算法的稳定性及其汇总
同样值的个体之间，如果不因为排序而改变相对次序，就是这个排序是有稳定性的；否则就没有
不具有稳定性的排序：选择排序、快速排序、堆排序；
具备稳定性的排序：冒泡排序、插入排序、归并排序、一切桶排序思想下的排序
[相等的时候不让交换，保持了稳定性]
目前没有找到时间复杂度O（
）,额外空间复杂度O（1），又稳定的排序
选择排序
从0~N-1位置上选一最小值，放0位置上……
冒泡排序
0~1上比较交换，1~2,2~3,3~4,4~5,5位置排好
0~1上比较交换，1~2,2~3,3~4 ,4位置排好
……
插入排序
0~0有序
0~1交换、有序
0~2交换、有序
| 时间复杂度 | 额外空间复杂度 | 稳定性 | |
| 选择 | O（ | O（1） | × |
| 冒泡 | O（ | O（1） | √ |
| 插入 | O（ | O（1） | √ |
| 归并 | O（ | O（N） | √ |
| 快排 | O（ | O（ | × |
| 堆 | O（ | O（1） | × |
）
）
）
）
）
）
）常见的坑
- 归并排序的额外空间复杂度可以变为O（1），但非常难，不需要掌握，有兴趣可以搜“归并排序内部缓存法”
- “原地归并排序”的帖子都是垃圾，会让归并排序的时间复杂度变成O（
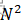） - 快排可以做到稳定性，但非常难，不需要掌握，可以搜“01 stable sort”
- 所有的改进都不重要，因为目前没有找到时间复杂度O（
），额外空间复杂度O（1），又稳定的排序 - 有一道题目是奇数放在数组左边，偶数放在数组右边，还要求原始的相对次序不变，碰到这个问题，可以怼面试官
工程上对排序的改进
- 充分利用O（
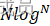）和O（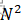
）排序各自的优势 - 稳定性的考虑
| 大样本量时 | 调度 快排 O（ |
| 小样本量时 | 插入 O（ |
）
）
