Yao, Y., Luo, Z., Li, S., Fang, T., Quan, L. (2018). MVSNet: Depth Inference for Unstructured Multi-view Stereo. In: Ferrari, V., Hebert, M., Sminchisescu, C., Weiss, Y. (eds) Computer Vision – ECCV 2018. ECCV 2018. Lecture Notes in Computer Science(), vol 11212. Springer, Cham. https://doi.org/10.1007/978-3-030-01237-3_47

摘要

作者提出了一种端到端深度学习架构，对多视图图像进行深度图推断。在网络中，作者首先提取深度视觉图像特征，然后通过可微分单应性变换在参考相机坐标系上构建三维代价体。接下来，应用三维卷积对初始深度图进行正则化和回归，然后用参考图像进行细化，最终输出推断的深度图。该框架使用基于方差的代价度量灵活地适应任意的n视图输入，该度量将多个特征映射到一个代价特征中。在大规模室内DTU数据集上对MVSNet进行了演示。通过简单的后处理，该方法不仅显著优于以前的最新技术，而且运行速度也快了好几倍。还在复杂的室外坦克和寺庙数据集上评估了MVSNet，在2018年4月18日之前，该方法在没有进行任何微调的情况下排名第一，显示出MVSNet具有很强的泛化能力。

1 引言

多视图立体视觉（MVS, Multi-view stereo）估计重叠图像的密集表示是计算机视觉领域研究了数十年的核心问题。传统的方法使用手工的相似度度量和工程正则化（例如，归一化互相关和半全局匹配）来计算对应的密集和恢复三维点。虽然这些方法在理想的传感器下显示了良好的结果，但它们存在一些共同的局限性。例如，场景的低纹理、镜面和反射区域使密集匹配难以处理，从而导致不完整的重建。在最近的MVS基准测试中报道，尽管目前最先进的算法在精度上表现得很好，但重建的完整性仍然有很大的改进空间。

最近卷积神经网络（CNNs）研究的成功也引发了人们对改进立体重建的兴趣。从概念上讲，基于学习的方法可以引入全局语义信息，如镜面和反射先验，以实现更鲁棒的匹配。有一些尝试在双视图立体匹配上，用基于学习的方式取代手工的相似度量或工程正则化。这些工作已经显示出了良好的结果，并在立体基准测试集中逐渐超过了传统的方法。事实上，立体匹配任务非常适合使用基于CNN的方法，因为图像对被预先纠正，因此问题成为不影响摄像机参数的水平像素级视差估计。

然而，直接将学习到的双视图立体视觉扩展到多视图场景并不简单。虽然可以简单地对所有选择的图像对进行立体匹配，然后将所有成对的重建合并到一个全局点云，但这种方法不能充分利用多视图信息，导致不准确的结果。与立体匹配不同，输入到MVS的图像可能是任意的相机几何形状，这给基于学习的方法带来了一个棘手的问题。

只有少数工作认识到这个问题，并尝试将CNN应用于MVS重建：SurfaceNet预先构造了彩色体素立方体（CVC, Colored Voxel Cubes），它将所有图像像素的颜色和摄像机信息结合到单个体积作为网络的输入。相比之下，基于学习的立体视觉机制（LSM, Learned Stereo Machine）直接利用可微分投影/非投影来实现端到端训练/推理。

然而，这两种方法都利用了规则网格的体积表示。由于3D体积巨大内存消耗的限制，他们的网络很难扩展： LSM只处理低体积分辨率的合成对象，SurfaceNet采用启发式分治策略，需要很长时间进行大规模重建。在2018年4月18日之前，现代MVS基准测试的主流仍被传统的方法所占据。

为此，作者提出了一种用于深度图推理的端到端深度学习架构，它每次计算一个深度图，而不是一次计算整个3D场景。与其它基于深度图的MVS方法类似，MVSNet以一个参考图像和几个源图像作为输入，并推断出参考图像的深度图。这里的关键是可微分单应性变换操作，它隐式地编码网络中的摄像机几何结构，从二维图像特征构建三维代价体，并实现端到端训练。

为了适应输入中任意数量的源图像，我们提出了一个基于方差的度量方法，它将多个特征映射到一个代价体特征中。这个代价体经过多尺度的三维卷积和回归出一个初始深度图。最后，利用参考图像对深度图进行细化，以提高边界区域的精度。

MVSNet和以前基于学习的方法之间有两个主要的区别。首先，为了进行深度图推断，MVSNet的3D代价体是建立在相机的坐标系之上，而不是常规的欧几里得空间。其次，MVSNet将MVS重建解耦到较小的每一个视图深度图估计问题上，这使得大规模重建成为可能。

2 相关基础

2.1 多视图立体视觉重建（MVS Reconstruction）

根据输出表示法，MVS方法可分为1)直接点云重建、2)体素重建、3)深度图重建。基于点云的方法直接基于三维点，通常依靠传播策略逐步强化重建。由于点云的传播是按顺序进行的，这些方法很难被完全并行化，而且通常需要很长的处理时间。基于体素的方法将三维空间划分为规则的网格，然后估计每个体素是否附着在表面上。这种表示方法的缺点是空间离散化误差和高内存消耗。相比之下，深度图是所有表示方式中最灵活的。它将复杂的MVS问题解耦为相对较小的每一幅视图的深度图估计问题，该问题一次只关注一个参考图像和几个源图像。此外，深度图可以很容易地融合到点云或体素重建上。根据最近的MVS基准测试，在2018年4月18日之前最好的MVS算法都是基于深度图的方法。

2.2 基于学习的立体视觉（Learned Stereo）

与使用传统的手工图像特征和匹配度量不同，最近的立体视觉研究使用深度学习技术进行成对的补丁匹配。Han等人首先提出了一个深度网络来匹配两个图像补丁。Zbontar等人和Luo等人使用学习到的特征进行立体匹配和半全局匹配（SGM）进行后处理。除了成对匹配代价外，基于学习的方法也应用于代价正则化。SGMNet学习调整SGM中使用的参数，而CNN-CRF 在网络中整合了条件随机场优化，用于端到端立体视觉学习。在2018年4月18日之前，最先进的方法是GCNet ，它应用3D CNN来规范代价体，并通过soft argmin操作回归视差。在KITTI数据集中有报道，基于学习的立体视觉方法，特别是端到端的学习算法，明显优于传统的立体视觉方法。

2.3 基于学习的多视图的立体视觉（Learned MVS）

在2018年4月18日之前，研究者们对基于学习的MVS方法的尝试较少。哈特曼等人提出了学习到的多补丁相似度来替代传统的MVS重建的代价度量。第一个基于学习的处理MVS问题的算法是SurfaceNet ，它通过复杂的体素级视图选择预先计算代价体，并使用三维CNN进行正则化和推断表面体素。与MVSNet最相关的方法是LSM，其中摄像机参数在网络中被编码为投影操作，以形成代价体，并使用3D CNN对一个体素是否属于某一表面进行分类。然而，由于体素表示的普遍缺点，SurfaceNet和LSM的网络被限制在小规模的重建。它们要么应用分治策略，要么只适用于具有低分辨率输入的合成数据。相比之下，MVSNet专注于每次为一个参考图像生成深度图，这使得MVSNet可以直接自适应地重建一个大型场景。

3 MVSNet

3.1 网络架构

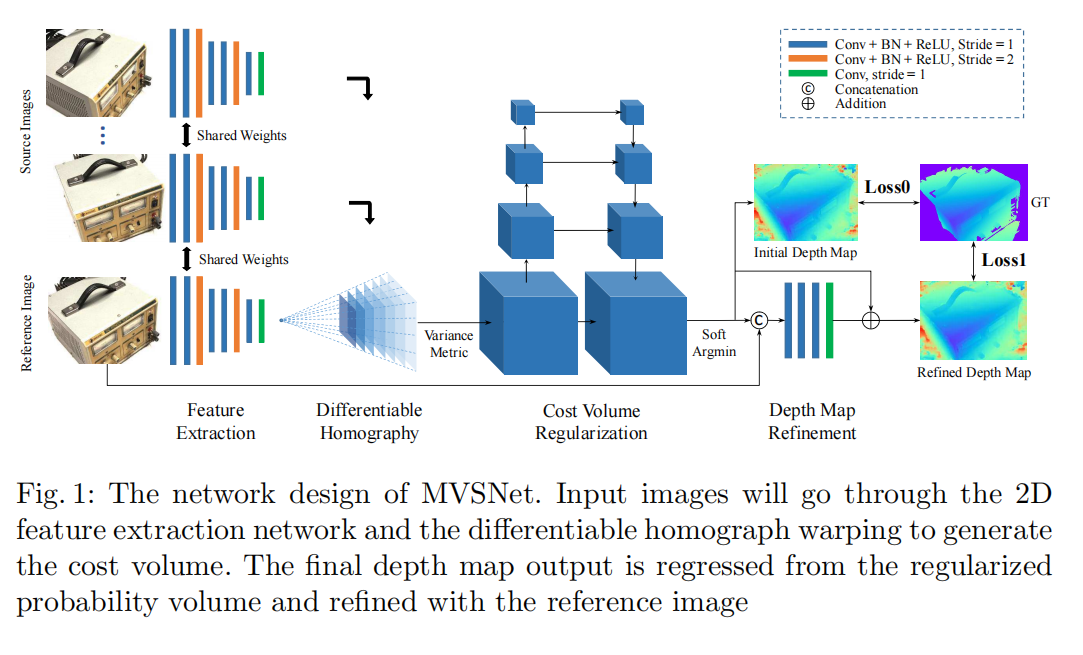
3.2 提取图片特征

MVSNet的第一步是提取N个输入图像的深度特征$(F_i{)}_{i=1}^N$进行密集匹配。采用八层二维CNN，将第3层和第6层的步长设置为2，将特征金字塔划分为三个尺度。在每个尺度内，应用两个卷积层来提取更高级别的图像表示。除了最后一层，每个卷积层之后都是一个批归一化（BN）层和一个校正后的线性单位（ReLU）。此外，类似于常见的匹配任务，参数在所有特征金字塔之间共享，以实现高效学习。二维网络的输出是32通道特征图，与输入图像相比，32通道特征图在各维度上缩小了4个。值得注意的是，虽然特征提取后图像帧缩小，但每个剩余像素的原始相邻信息已经被编码到32通道像素描述符中，防止了密集匹配丢失有用的背景信息。与简单地对原始图像进行密集匹配相比，提取的特征图显著提高了重建质量。

3.3 构建代价体

接下来，从提取的特征图和输入相机中建立1个3D代价体。虽然之前的工作使用规则网格划分空间，对于我们的深度地图推断任务，我们在参考相机坐标系上构造代价体。为简单起见，下面$I_1$表示为参考图像，$(I_i{)}_{i=2}^N$表示源图像，$(K_i，R_i，t_i{)}_{i=1}^N$表示与特征图对应的相机内参、旋转矩阵和平移。

3.4 可微分单应性变换（Differentiable Homography）

将所有特征图转换成参考相机的不同前平行平面，形成N个特征体$(V_i{)}_{i=1}^N$。在深度d下，坐标映射从变换后的特征图$V_i(d)$到$F_i$通过平面变换$x^{\prime }\sim H_i(d)\cdot x$，其中“∼”表示投影等式，$H_i(d)$表示第i个特征图与参考特征图在深度d处的单应性矩阵。设n1为参考相机的主轴，单应性用3×3矩阵表示：
$${\mathbf{H}}_i(d)={\mathbf{K}}_i\cdot {\mathbf{R}}_i\cdot \left(\mathbf{I}-\frac{\left({\mathbf{t}}_1-{\mathbf{t}}_i\right)\cdot {\mathbf{n}}_1^T}{d}\right)\cdot {\mathbf{R}}_1^T\cdot {\mathbf{K}}_1^T(1)$$
不失一般性，参考特征图F1的单应性本身是一个3×3单位矩阵。变换过程类似于经典的平面扫描立体视觉算法，除了可微双线性线性插值用于从特征图$(F_i{)}_{i=1}^N$采样像素而不是图像$(I_i{)}_{i=1}^N$。作为连接二维特征提取和三维正则化网络的核心步骤，以可微的方式实现了变换操作，实现了深度图推理的端到端训练。

3.4 代价度量

接下来，将多个特征体$(V_i{)}_{i=1}^N$聚合为一个代价体C。为了适应任意数量的输入视图，作者提出了一个基于方差的代价度量M用于N视图相似性度量。设W、H、D、F为输入图像的宽度、高度、深度采样数和特征图的通道数，V = W/4·H/4·D·F为特征体大小，成本度量被定义为映射$\mathcal{M}:\underset{N}{\underbrace{{\mathbb{R}}^V\times \cdots \times {\mathbb{R}}^V}}\to {\mathbb{R}}^V$：
$$\mathbf{C}=\mathcal{M}\left({\mathbf{V}}_1,\cdots ,{\mathbf{V}}_N\right)=\frac{{\sum }_{i=1}^N{\left({\mathbf{V}}_i-\overline{{\mathbf{V}}_i}\right)}^2}{N}(2)$$
其中$\overline{{\mathbf{V}}_i}$是所有特征体的平均体，上面所有操作都是按元素个体操作。
大多数传统的MVS方法以启发式的方式聚合参考图像和所有源图像之间的配对代价。相反，MVSNet的度量设计遵循的原则是所有的视图都应该对匹配成本的贡献相同，而不优先考虑参考图像。在2018年4月18日之前的工作应用了多个CNN层的平均操作来推断多补丁相似性。在这里，作者选择了“方差”操作，因为“均值”操作本身没有提供关于特征差异的信息，而且它们的网络需要CNN前层和CNN后层来帮助推断相似性。相比之下，基于方差的代价度量明确地测量了多视图特征的差异。