已知数据集D中有9个数据点,分别是(1,2),(2,3), (2,1), (3,1),(2,4),(3,5),(4,3),(1,5),(4,2)。采用K-Means算法进行聚类,k=2,设初始中心点为(1.1,2.2),(2.3,3.5)。 试模拟K-Means算法的一次迭代过程,即先计算样本点到类中心点的距离,然后把样本点划分到最近的类中,最后更新类中心点的坐标
数据集合D:{(1,2),(2,3),(2,1),(3,1),(2,4),(3,5),(4,3),(1,5),(4,2)} 初始中心点: C1=(1.1,2.2),C2=(2.3,3.5) 计算每个数据点到两个中心点的距离,并将其划分到距离最近的类中。假设我们使用欧氏距离:
数据集合D:{(1,2),(2,3),(2,1),(3,1),(2,4),(3,5),(4,3),(1,5),(4,2)} 初始中心点: C1=(1.1,2.2),C2=(2.3,3.5) 计算每个数据点到两个中心点的距离,并将其划分到距离最近的类中。假设我们使用欧氏距离:
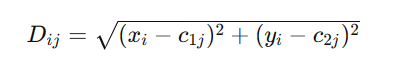
计算每个数据点到两个中心点的距离:

将每个数据点划分到距离最近的类中。这里我们用1和2表示两个类:
C={1,2,1,1,2,2,2,2,2}
更新类中心点的坐标,即计算每个类的均值:
C1=((1+2+3)/3,(2+1+1)/3)≈(2,1.3)
C2=((2+2+3+4+1+4)/6,(3+4+5+3+5+2)/6))≈(2.6,3.6)





:集成SpringBoot)
)
》)


)







![[C/C++]数据结构 链表(单向链表,双向链表)](http://pic.xiahunao.cn/[C/C++]数据结构 链表(单向链表,双向链表))
