Hi,你好。我是茶桁。

上节课，我们讲了多层神经网络的原理，并且明白了，数据量是层级无法超过3层的主要原因。

然后我们用一张图来解释了整个链式求导的过程：

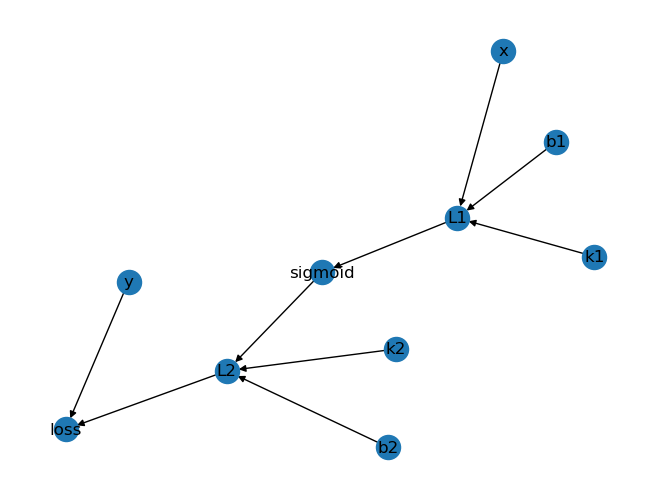
那么，我们如何将这张图里的节点关系来获得它的求导过程呢？

假如我们现在定义一个函数get_output:

def get_output(graph, node):outputs = []for n, links in graph.items():if node == n: outputs += linksreturn outputs
get_output(computing_graph, 'k1')---
['L1']

我们可以根据k1获得l1。

来，让我们整理一下思路，问：如何获得k1的偏导：

1. 获得k1的输出节点
2. 获得k1输出节点的输出节点
3. …直到我们找到最后一个节点

computing_order = []target = 'k1'
out = get_output(computing_graph, target)[0]
computing_order.append(target)while out:computing_order.append(out)out = get_output(computing_graph, out)if out: out = out[0]computing_order---
['k1', 'L1', 'sigmoid', 'L2', 'loss']

我们从k1出发，它可以获得这么一套顺序。那么现在如果要计算k1的偏导，我们的这个偏导顺序就等于从后到前给它求解一遍。

order = ''for i, n in enumerate(computing_order[:-1]):order += '*∂{} / ∂{}'.format(n, computing_order[i+1])order
---
'*∂k1 / ∂L1*∂L1 / ∂sigmoid*∂sigmoid / ∂L2*∂L2 / ∂loss'

现在k1的求导顺序计算机就给它自动求解出来了, 我们把它放到了一个图里面，然后它自动就求解出来了。只不过唯一的问题是现在这个order是反着的，需要把它再反过来。

for i, n in enumerate(computing_order[:-1]):order.append((computing_order[i + 1], n))# order += ' * ∂{} / ∂{}'.format(n, computing_order[i+1])' * '.join(['∂{}/∂{}'.format(a, b) for a, b in order[::-1]])---
'∂loss/∂L2 * ∂L2/∂sigmoid * ∂sigmoid/∂L1 * ∂L1/∂k1'

这个过程用计算机实现之后，我们就可以拿它来看一下其他的参数，比如说b1:

computing_order = []target = 'b1'
out = get_output(computing_graph, target)[0]
computing_order.append(target)while out:computing_order.append(out)out = get_output(computing_graph, out)if out: out = out[0]order = []for i, n in enumerate(computing_order[:-1]):order.append((computing_order[i + 1], n))# order += ' * ∂{} / ∂{}'.format(n, computing_order[i+1])' * '.join(['∂{}/∂{}'.format(a, b) for a, b in order[::-1]])---
'∂loss/∂L2 * ∂L2/∂sigmoid * ∂sigmoid/∂L1 * ∂L1/∂b1'

k2:

...
target = 'k2'
...---
'∂loss/∂L2 * ∂L2/∂k2'

到这里， 我们能够自动的求解各个参数的导数了。

然后我们将其封装一下，然后循环一下每一个参数：

def get_paramter_partial_order(p):...target = p...return ...for p in ['b1', 'k1', 'b2', 'k2']:print(get_paramter_partial_order(p))---
∂loss/∂L2 * ∂L2/∂sigmoid * ∂sigmoid/∂L1 * ∂L1/∂b1
∂loss/∂L2 * ∂L2/∂sigmoid * ∂sigmoid/∂L1 * ∂L1/∂k1
∂loss/∂L2 * ∂L2/∂b2
∂loss/∂L2 * ∂L2/∂k2

到这一步你就能够发现，每一个参数的导数的偏导我们都可以求解了。而且我们还发现一个问题，不管是['b1', 'k1', 'b2', 'k2']中的哪一个，我们都需要求求解∂loss/∂L2。

所以现在如果有一个内存能够记录结果，先把∂loss/∂L2的值求解下来，把这个值先存下来，只要算出来这一个值之后，再算['b1', 'k1', 'b2', 'k2']的时候直接拿过来就行了。

也就是说我们首先需要记录的就是这个值，其次，如果我们把L2和sigmoid的值记下来，求解b1和k1的时候直接拿过来用就行，不需要再去计算一遍，这个时候我们的效率就会提升很多。

首先把共有的一个基础∂loss/∂L2计算了, 第二步,有了∂loss/∂L2，把∂L2/∂sigmoid再记录一遍， 第三个是∂sigmoid/∂L1,然后后面以此就是∂L1/∂b1, ∂L1/∂k1，∂L2/∂b2, ∂L2/∂k2。

现在的问题就是就是怎么样让计算机自动得到这个顺序，计算机得到这个顺序的时候，把这些值都存在某个地方。

这个所谓的顺序就是我们非常重要的一个概念，在计算机科学，算法里面非常重要的一个概念：「拓朴排序」。

那拓朴排序该如何实现呢？来，我们一起来实现一下：

首先，我们定义一个方法，咱们输入的是一个图，这个图的定义方式是一个Dictionary，然后里面有一些节点，里面的很多个连接的点：

def topologic(graph):'''graph: dict{node: [node1, node2, ..., noden]}'''return None

因为我们要把它的结果存在一个变量里边，当我们不断的检查看这个图，看看它是否为空，然后我们来定义两个存储变量：

def topologic(graph):sorted_node = []while graph:all_inputs = []all_outputs = list(graph.keys())return sorted_node

这里的两个变量，all_inputs和all_outputs, 一个是用来存储所有的输入节点，一个是存储所有的输出节点。

我们还记得我们那个图的格式是什么样的吗？

computing_graph = {'k1': ['L1'],'b1': ['L1'],'x': ['L1'],'L1':['sigmoid'],'sigmoid': ['L2'],'k2': ['L2'],'b2': ['L2'],'L2': ['loss'],'y': ['loss']
}

我们看这个数据，那所有的输出节点是不是就是其中的key啊？

打比方说，我们拿一个短小的数据来做示例：

simple_graph = {'a': [1, 2],'b': [3, 4]
}list(simple_graph.keys())---
['a', 'b']

那我们这样就拿到了输出节点，并将其放在了一个列表内。

这里说点其他的，Python 3.9及以上的版本其实都实现了自带拓朴排序，但是如果你的Python版本较低，那还是需要自己去实现。这个也是Python 3.9里面一个比较重要的更新。

那为什么我们的value定义的是一个列表呢？这是因为这个key，也就是输出值可能会输出到好几个函数里面，因为我们现在拿的是一个比较简单的模型，但是在真实场景中，有可能会输出到更多的节点中。

这里，就获得了所有有输入的节点， simple_graph中，a输出给了[1,2], b输出给了[2,3]。

那我们怎么获得所有输入的节点呢？那就应该是value。

list(simple_graph.values())---
[[1, 2], [3, 4]]

这样就获得所有有输入的节点。然后就是怎么样把这两个list合并。可以有一个简单的方法，一个叫做reduce的方法。

reduce(lambda a, b: a+b, list(simple_graph.values()))---
[1, 2, 3, 4]

这样就把它给它连起来了。

那我们还需要找一个，就是只有输出没有输入的节点，这些该怎么去找呢？其实也就是我们的[k1, b1, k2, b2, y]这些值。

来，我们还是拿刚才的simple_graph来举例，但是这次我们改一下里面的内容：

simple_graph = {'a': ['a', 2],'b': ['b', 4]
}a = list(simple_graph.keys())
b = reduce(lambda a, b: a+b, list(simple_graph.values()))print(list(set(b) - set(a)))---
[2, 4]

我们没有用循环，而是将其变成了一个集合，然后利用集合的加减来做。

我们的实际代码就可以这样写：

def topologic(graph):sorted_node = []while graph:all_inputs = reduce(lambda a, b: a+b, list(graph.values()))all_outputs = list(graph.keys())all_inputs = set(all_inputs)all_outputs = set(all_outputs)need_remove = all_outputs - all_inputsreturn sorted_node

那现在我们继续往后，如果找到了这些只有输出没有输入的节点之后，我们做一个判断，然后定义一个节点，用来保存随机选择的节点：

if len(need_remove) > 0:node = random.choice(list(need_remove))

这个时候x, b, k, y都有可能，那么我们随机找一个就行。然后将这个找到的节点从graph给它删除。并且将其插入到sorted_node中去，并且返回出来。

    if ...:node = random.choice(list(need_remove))graph.pop(node)sorted_node.append(node)return sorted_node

然后这里还会出一个小问题，我们还是拿一个示例来说：

simple_graph = {'a': ['sigmoid'],'b': ['loss'],'c': ['loss']
}simple_graph.pop('b')
simple_graph---
{'a': ['sigmoid'], 'c': ['loss']}

看，我们在删除node的时候，其所对应的value也就一起删除了，那这个时候，我们最后的输出列表里会丢失最后一个node。所以，我们在判断为最后一个的时候，需要额外的将其加上, 放在pop方法执行之前。那我们整个代码需要调整一下先后顺序。

def topologic(graph):sorted_node = []while graph:...if len(need_remove) > 0:node = random.choice(list(need_remove))sorted_node.append(node)if len(graph) == 1: sorted_node += graph[node]         graph.pop(node)return sorted_node

现在其实这个代码就已经OK了，我们来再加几句话：

...
if len(need_remove) > 0:...for _, links in graph.items():if node in links: links.remove(node)
else:raise TypeError('This graph has circle, which cannot get topological order.')
...

我们把它的连接关系，例如现在选择了k1，我们要把k1的连接关系从这些里边给它删掉。

遍历一下graph，遍历的时候如果删除的node在它的输出里边，我们就把它删除。

加上else判断，如果图不是空的，但是最终没有找到，也就是这两个集合作减法，但是得到一个空集，没有找到，那我们就来输出一个错误：This graph has circle, which cannot get topological order.

现在我们可以来实验一下了：

x, k, b, linear, sigmoid, y, loss = 'x', 'k', 'b', 'linear', 'sigmoid', 'y', 'loss'
test_graph = {x: [linear],k: [linear],b: [linear],linear: [sigmoid],sigmoid: [loss],y: [loss]
}topologic(test_graph)---
['x', 'b', 'k', 'y', 'linear', 'sigmoid', 'loss']

好， 现在让我们来声明一个class node:

class Node:pass

然后我们先来抽象一下这些节点：

## Our Simple Model Elementsnode_x = Node(inputs=None, outputs=[node_linear])
node_y = Node(inputs=None, outputs=[node_loss])
node_k = Node(inputs=None, outputs=[node_linear])
node_b = Node(inputs=None, outputs=[node_linear])
node_linear = Node(inputs=[node_x, node_k, node_b], outputs=[node_sigmoid])
node_sigmoid = Node(inputs=[node_linear], outputs=[node_loss])
node_loss = Node(inputs=[node_sigmoid, node_y], outputs=None)

现在咱们就把图中每个节点已经给它抽象好了，但是我们发现节点写成这个样子代码是比较冗余。打比方说：node_linear = Node(input=[node_x, node_k, node_b], outputs=[node_sigmoid])， 既然我们已经告诉程序node_linear这个节点的输入是[node_x, node_k, node_b]， 那其实也就是告诉程序这些节点的输出是node_linear。

好，我们接下来要在class Node里定义一个方法:

def __init__(self, inputs, outputs):self.inputs = inputsself.outputs = outputs

现在我们根据上面对代码冗余的分析，可以加上这样简单的一句：

def __init__(self, inputs=[]):self.inputs = inputsself.outputs = []for node in inputs:node.outputs.append(self)

把这句加上之后, 就可以只在里面输入inputs就行了，不用再输入outputs，代码就变得简单多了:

## Our Simple Model Elements
### version - 02
node_x = Node()
node_y = Node()
node_k = Node()
node_b = Node()
node_linear = Node(inputs=[node_x, node_k, node_b])
node_sigmoid = Node(inputs=[node_linear])
node_loss = Node(inputs=[node_sigmoid, node_y])

我们是把每个节点给它做出来了，那么怎么样能够把这个节点给它像串珠子一样串起来变成一张图呢？

其实我们只要去考察所有的边沿节点就可以了，把所有的x，y，k和b这种外层的函数给个变量：

need_expend = [node_x, node_y, node_k, node_b]

咱们再生成一个变量，这个变量是用来通过外沿这些节点，把连接图给生成出来。

computing_graph = defaultdict(list)while need_expend:n = need_expend.pop(0)if n in computing_graph: continuefor m in n.outputs:computing_graph[n].append(m)need_expend.append(m)

while里面，当外沿节点的list不为空的时候，我们就在里面来取一个点，我们就取第一个吧，取出来并删除。

然后如果这个点我们已经考察过了， 那就continue，如果没有，我们对于所有的这个n里边的outputs，插入到computing_graph的n的位置。再插入到外沿节点的list内。因为我们现在多了一个扩充节点，所以我们需要给插入进去。

比方说我们这次找出来了linear，把linear也加到这个需要扩充的点一行，然后就可以从linear再找到sigmoid了。

来，我们看下现在的这个computing_graph:

computing_graph---
defaultdict(list,{<__main__.Node at 0x12053e080>: [<__main__.Node at 0x12053dc30>],<__main__.Node at 0x12053e9b0>: [<__main__.Node at 0x12053ef50>],<__main__.Node at 0x12053d510>: [<__main__.Node at 0x12053dc30>],<__main__.Node at 0x12053c280>: [<__main__.Node at 0x12053dc30>],<__main__.Node at 0x12053dc30>: [<__main__.Node at 0x1202860e0>],<__main__.Node at 0x1202860e0>: [<__main__.Node at 0x12053ef50>]})

这样就获得出来了，其实是把它变成了刚刚的那个图。这样呢，我们就可以应用topologic来进行拓朴排序了。

topologic(computing_graph)---
[<__main__.Node at 0x12053c280>,<__main__.Node at 0x12053d510>,<__main__.Node at 0x12053e080>,<__main__.Node at 0x12053e9b0>,<__main__.Node at 0x12053dc30>,<__main__.Node at 0x1202860e0>,<__main__.Node at 0x12053ef50>]

但是我们打出来的内容都是一些内存地址，我们还需要改一下这个程序。我们在我们的class Node里多增加一个方法，用于return它的名字：

def __init__(self, inputs=[], name=None):...self.name = namedef __repr__(self):return 'Node:{} '.format(self.name)

这样之后，我们还需要改一下节点，在里面增加一个变量name=''。

node_x = Node(name='x')
...
node_loss = Node(inputs=[node_sigmoid, node_y], name='loss')

每一个都需要加上，我用...简化了代码。

然后我们再来看：

topologic(computing_graph)---
[Node:k , Node:x , Node:b , Node:linear , Node:sigmoid , Node:y , Node:loss ]

然后我们来将这段封装起来，变成一个函数：

feed_dict = {node_x: 3, node_y: random.random(),node_k: random.random(),node_b: 0.38
}def convert_feed_dict_to_graph(feed_dict):need_expend = [n for n in feed_dict]...return computing_graph

一般来说，很多大厂在建立代码的时候，x, y, k, b这种东西会被称为placeholder， 我们创建的need_expend会被称为是feed_dict。所以我们做了这样一个修改，将need_expend拿到方法里取重新获取。

这些节点刚开始的时候没有值，那我们给它一个初始值，我这里的值都是随意给的。

这样，就不仅把最外沿的节点给找出来了，而且还把值给他送进去了，相对来说就会更简单一些。所有定义出来的节点，我们都可以把它变成图关系。

topologic(convert_feed_dict_to_graph(feed_dict))---
[Node:k , Node:y , Node:b , Node:x , Node:linear , Node:sigmoid , Node:loss ]

咱们现在再定一个点，我们用一个变量存起来:

sorted_nodes = topologic(convert_feed_dict_to_graph(feed_dict))

那么咱们现在来模拟一下它的计算过程，模拟神经网络的计算过程。

class Node:...def fowward(self):print('I am {}, I calculate myself value!!!'.format(self.name))for node in sorted_nodes:node.forward()---
I am y, I calculate myself value!!!
I am x, I calculate myself value!!!
I am b, I calculate myself value!!!
I am k, I calculate myself value!!!
I am linear, I calculate myself value!!!
I am sigmoid, I calculate myself value!!!
I am loss, I calculate myself value!!!

我们在Node里定义了一个方法forward，从前往后运算，这个时候我们在每个里面加一个向前运算。

这个就是拓朴排序的作用，经过排序之后，那需要在后面计算的节点，就一定会放在后面再进行计算。

好，那我们现在需要区分两个内容，一个是被赋值的内容，一个是需要计算的内容。

刚才我们说过，在大厂的这些地方，x,y,k,b这种东西都被定义为占位符，那我们来修改一下代码：

class Node:def __init__(self, inputs=[], name=None):...def forward(self):print('I am {}, 我需要自己计算自己的值。'.format(self.name))...class Placeholder(Node):def __init__(self, name=None):Node.__init__(self, name = name)def forward(self):print('I am {}, 我已经被人为赋值了。'.format(self.name))def __repr__(self):return 'Node:{} '.format(self.name)### version - 02
node_x = Placeholder(name='x')
node_y = Placeholder(name='y')
node_k = Placeholder(name='k')
node_b = Placeholder(name='b')
node_linear = Node(inputs=[node_x, node_k, node_b], name='linear')
node_sigmoid = Node(inputs=[node_linear], name='sigmoid')
node_loss = Node(inputs=[node_sigmoid, node_y], name='loss')

我们创建了一个Placeholder类，继承了Node, 然后我们取修改初始化方法，它是是没有input的，只有一个name。

然后forward我们改一下，改成打印已经被赋值的语句。父类Node里的forward也改一下，改成需要自己计算自己的值。

那我们这个时候将赋值的四个节点改成调用Placeholder。

接下来，我们需要修改convert_feed_dict_to_graph方法了：

def convert_feed_dict_to_graph(feed_dict):...while need_expend:...if isinstance(n, Placeholder): n.value = feed_dict[n]......

我们来检查这个节点是否是Placeholder，如果是的话，将当前的feed_dict赋值给n.value。来看下结果：

for node in sorted_nodes:node.forward()---
I am b, 我已经被人为赋值了。
I am x, 我已经被人为赋值了。
I am k, 我已经被人为赋值了。
I am y, 我已经被人为赋值了。
I am linear, 我需要自己计算自己的值。
I am sigmoid, 我需要自己计算自己的值。
I am loss, 我需要自己计算自己的值。

好，到现在为止，咱们只是打了一段文字，问题是对于linear, sigmoid和loss, 到底是怎么计算的呢？

这个问题，咱们放到下一节课里面去讲，现在咱们这篇文章已经超标了，目测应该超过万字了吧。

好，下节课记得来看咱们具体如何在实现拓朴排序后将计算加进去。