455.分发饼干

题目：

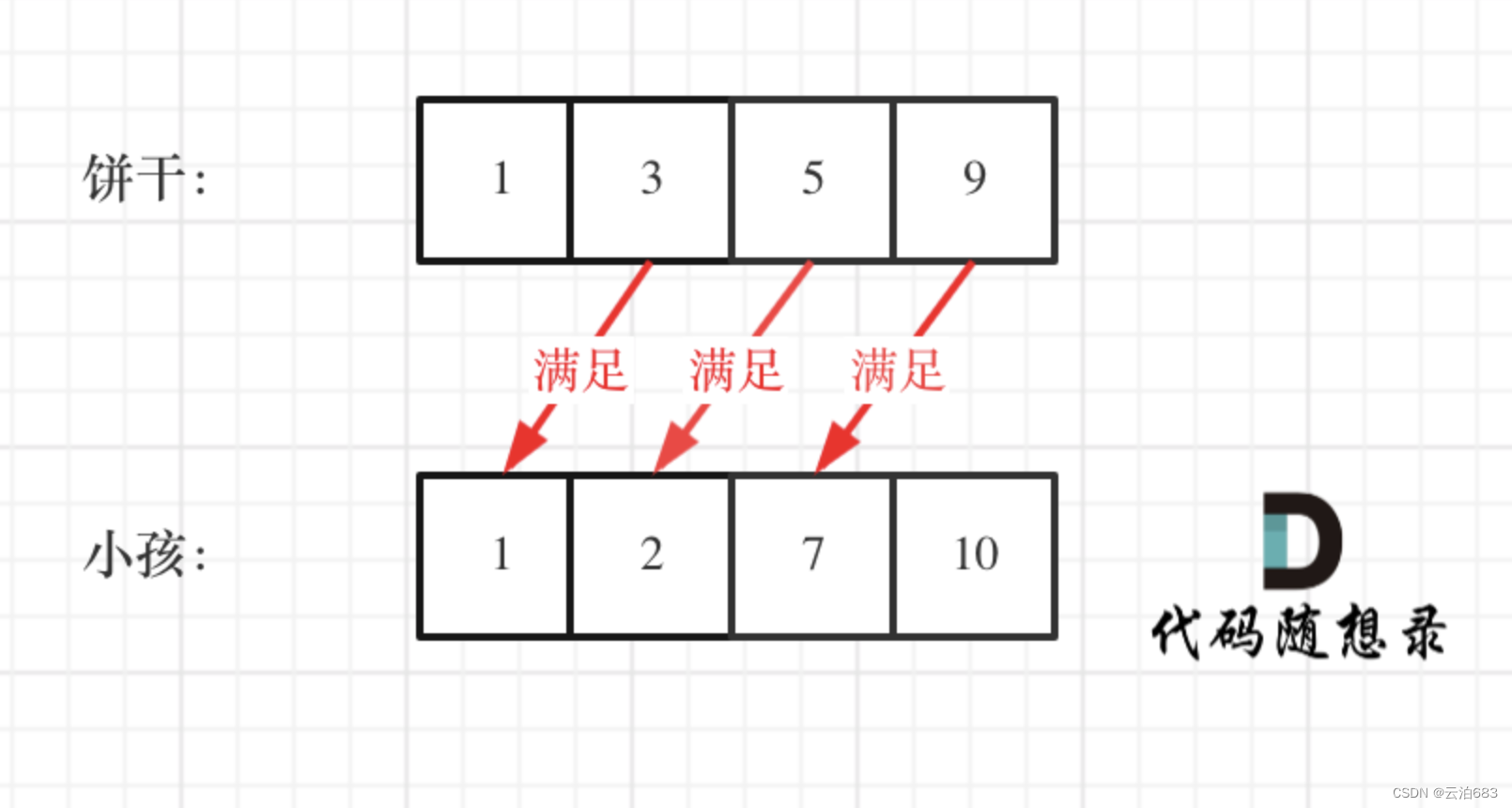
小朋友胃口值数组g[i]，饼干尺寸数组 s[j]，当饼干尺寸s[j]大于等于g[i]的时候，对应小朋友被满足，小朋友每一个最多一块饼干 ，求给定条件下最多被满足的小朋友数量。

思路：

局部最优：尺寸最大的饼干先分给胃口最大的小朋友

全局最优：然后不断饼干第二大尺寸，胃口第二大小朋友，不能一次吃饱的不给吃，达成全局最优

具体做法就是饼干数组和小孩数组排序，然后从后向前遍历小孩数组，用大饼干优先满足胃口大的，并统计满足小孩数量。

class Solution {
public:int findContentChildren(vector<int>& g, vector<int>& s) {sort(g.begin(), g.end());sort(s.begin(), s.end());int index = s.size() - 1; // 饼干数组的下标int result = 0;for (int i = g.size() - 1; i >= 0; i--) { // 遍历胃口if (index >= 0 && s[index] >= g[i]) { // 遍历饼干result++;index--;}}return result;}
};

 如果饼干尺寸大于等于胃口，结果+1，饼干向小尺寸继续遍历，胃口向小胃口小孩继续遍历。

如果饼干尺寸小于胃口，那么胃口继续向小胃口小孩遍历（胃口和饼干都经过排序）

也就是从大到小尺寸饼干满足胃口从大到小排序的小孩，饼干没满足小孩了，就下一个小孩，没小孩了就返回结果。