P1941 飞扬的小鸟

Description

Flappy Bird 是一款风靡一时的休闲手机游戏。玩家需要不断控制点击手机屏幕的频率来调节小鸟的飞行高度，让小鸟顺利通过画面右方的管道缝隙。如果小鸟一不小心撞到了水管或者掉在地上的话，便宣告失败。

为了简化问题，我们对游戏规则进行了简化和改编:

游戏界面是一个长为 $n$，高为 $m$ 的二维平面，其中有 $k$ 个管道（忽略管道的宽度）。

小鸟始终在游戏界面内移动。小鸟从游戏界面最左边任意整数高度位置出发，到达游戏界面最右边时，游戏完成。

小鸟每个单位时间沿横坐标方向右移的距离为 $1$，竖直移动的距离由玩家控制。如果点击屏幕，小鸟就会上升一定高度 $x$，每个单位时间可以点击多次，效果叠加；如果不点击屏幕，小鸟就会下降一定高度 $y$。小鸟位于横坐标方向不同位置时，上升的高度 $x$ 和下降的高度 $y$ 可能互不相同。

小鸟高度等于 $0$ 或者小鸟碰到管道时，游戏失败。小鸟高度为 $m$ 时，无法再上升。

现在,请你判断是否可以完成游戏。如果可以，输出最少点击屏幕数；否则，输出小鸟最多可以通过多少个管道缝隙。

Input

第 $1$ 行有 $3$ 个整数 $n,m,k$，分别表示游戏界面的长度，高度和水管的数量，每两个整数之间用一个空格隔开；

接下来的 $n$ 行，每行 $2$ 个用一个空格隔开的整数 $x$ 和 $y$，依次表示在横坐标位置 $0\sim n-1$ 上玩家点击屏幕后，小鸟在下一位置上升的高度 $x$，以及在这个位置上玩家不点击屏幕时，小鸟在下一位置下降的高度 $y$。

接下来 $k$ 行，每行 $3$ 个整数 $p,l,h$，每两个整数之间用一个空格隔开。每行表示一个管道，其中 $p$ 表示管道的横坐标，$l$ 表示此管道缝隙的下边沿高度，$h$ 表示管道缝隙上边沿的高度（输入数据保证 $p$ 各不相同，但不保证按照大小顺序给出）。

Output

共两行。

第一行，包含一个整数，如果可以成功完成游戏，则输出 $1$，否则输出 $0$。

第二行，包含一个整数，如果第一行为 $1$，则输出成功完成游戏需要最少点击屏幕数，否则，输出小鸟最多可以通过多少个管道缝隙。

Sample #1

Sample Input #1

10 10 6 
3 9  
9 9  
1 2  
1 3  
1 2  
1 1  
2 1  
2 1  
1 6  
2 2  
1 2 7 
5 1 5 
6 3 5 
7 5 8 
8 7 9 
9 1 3

Sample Output #1

1
6

Sample #2

Sample Input #2

10 10 4 
1 2  
3 1  
2 2  
1 8  
1 8  
3 2  
2 1  
2 1  
2 2  
1 2  
1 0 2 
6 7 9 
9 1 4 
3 8 10

Sample Output #2

0
3

Hint

如下图所示，蓝色直线表示小鸟的飞行轨迹，红色直线表示管道。

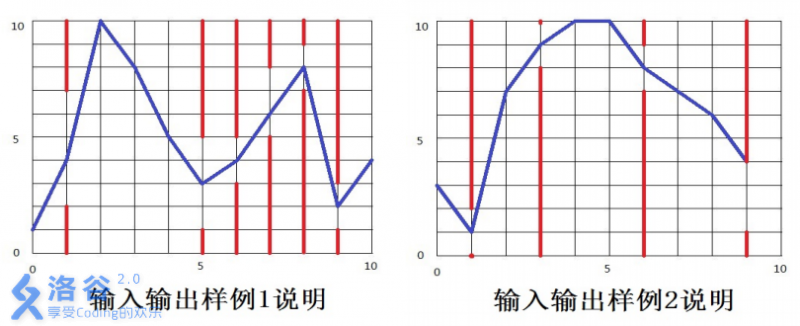
Constraints

对于 $30\%$ 的数据：$5\le n\le 10,5\le m\le 10,k=0$，保证存在一组最优解使得同一单位时间最多点击屏幕 $3$ 次；

对于 $50\%$ 的数据：$5\le n\le 20,5\le m\le 10$，保证存在一组最优解使得同一单位时间最多点击屏幕 $3$ 次；

对于 $70\%$ 的数据：$5\le n\le 1000,5\le m\le 100$；

对于 $100\%$ 的数据：$5\le n\le 10000$，$5\le m\le 1000$，$0\le k<n$，$0<x,y<m$，$0<p<n$，$0\le l<h\le m$， $l+1<h$。

---

Solution

对于此题，分为 $2$ 种情况：

1. 对于位置 $i$ 不按上升键，此时会下降 $y_i$
2. 对于位置 $i$ 按 $k$ 次上升键，此时会上升 $k\cdot x_i$

故，可以由 $01$ 背包 与 完全背包 融合来解决。

考虑设计状态 $f_{i,j}$ 表示在第 $i$ 个位置，高度为 $j$ 的最小操作次数

$70\mathrm{pts}$ 做法

转移分为两种情况（如下）：
$$f_{i,j}=\{\begin{array}{llc}& f_{i-1,j+y_i}& j+y_i\le m\\ & f_{i-1,j-k\cdot x_i}+k& j-k\cdot x_i\ge 1\end{array}$$
若在 $i$ 位置一次不按，则从 $i-1$ 位置到 $i$ 位置，会下降 $y_i$ 个单位，对应着 $i-1$ 位置的高度比当前会高 $y_i$ 个单位。

若在 $j$ 位置按 $k$ 次，则从 $i-1$ 位置到 $i$ 位置，会上升 $k\cdot x_i$ 个单位，对应着 $i-1$ 位置的高度比当前高度会低 $k\cdot x_i$ 个高度。

时间复杂度：$O(n{m}^2)$

---

$100pts$ 做法

对于上述式子采取与完全背包优化方式类似的方法来优化：

将式子展开：
$$f_{i,j}=\{\begin{array}{ll}& f_{i-1,j+y_i}\\ & f_{i-1,j-x_i}+1,f_{i-2,j-2\cdot x_i}+2,f_{i-3,j-3\cdot x_i}+3,\dots \end{array}$$
在观察 $f_{i,j-x_i}$ 的式子：
$$f_{i,j-x_i}=\{\begin{array}{ll}& f_{i-1,j-x_i+y_i}\\ & f_{i-2,j-2\cdot x_i}+1,f_{i-3,j-3\cdot x_i}+2,\dots \end{array}$$
此时，我们会发现第 $2$ 种情况的式子惊奇的相似，只是少了一项 $f_{i-1,j-x_i}$，且每一项都少了一个 $1$，故考虑借用数组 $g_{i,j}$ 表示 $\min (f_{i-1,j-x_i},f_{i-1,j-2\cdot x_i,\dots })$

由上面可得出 $g$ 数组的转移方程：
$$g_{i,j}=\min (g_{i-1,j-x_i}+1,f_{i-1,j-x_i}+1)$$
含义就是用 $f_{i,j-x_i}$ 的第 $2$ 种情况 $+1$，再补上少了的一部分 $f_{i-1,j-x_i}+1$

这样对于 $f_{i,j}$ 转移如下：$f_{i,j}=\min (f_{i-1,j+y_i},g_{i,j})$

时间复杂度：$O(nm)$

---

空间优化

由于观察发现 $g$ 数组只用到了坐标 $i$，所以这一维可以去掉

---

细节点播

对于 $f_{i,m}$ 需要特殊处理，因为 小鸟高度为 $m$ 时，无法再上升，所以会停留在 $m$，故这个位置可以有 $i-1$ 位置上的任何一个高度转移而来。

即：$f_{i,m}=\min (f_{i-1,j}+\lceil \frac{m-j}{x_i}\rceil )$

但是特别注意 $j=m$ 时，而 $\lceil \frac{m-j}{x_i}\rceil$ 会是 $0$，如果是 $0$ 那么还是会掉下去的，所以要特殊处理 $j=m$ 的情况：$f_{i,m}=f_{i-1,m}+1$

或者是不特殊处理：$f_{i,m}=\min (f_{i-1,j}+\max (1,\lceil \frac{m-j}{x_i}\rceil ))$

$\mathrm{Attention}:$ 只有当上面没有管道的时候，才需要处理。

---

结果输出

枚举所有的 $j$，取 $f_{n,j}$ 的最小值。

如果无法到达，则 $i$ 总大到小枚举，枚举 $j$ 确定是否可以到达，如果可以，统计前方有多少个管子输出即可。

---

Code

#include <iostream>
#include <cstring>
#define int long longusing namespace std;typedef pair<int, int> PII;const int SIZE = 1e4 + 10, INF = 0x3f3f3f3f3f3f3f3f;int N, M, K;
int X[SIZE], Y[SIZE];
int L[SIZE], H[SIZE];
int F[SIZE][SIZE], G[SIZE];signed main()
{cin.tie(0);cout.tie(0);ios::sync_with_stdio(0);cin >> N >> M >> K;for (int i = 1; i <= N; i ++)cin >> X[i] >> Y[i];int Pos, l, h;while (K --){cin >> Pos >> l >> h;L[Pos] = l, H[Pos] = h;}memset(F, 0x3f, sizeof F);for (int i = 1; i <= M; i ++)F[0][i] = 0;for (int i = 1; i <= N; i ++){memset(G, 0x3f, sizeof G);for (int j = 1; j <= M; j ++){if (j > X[i]) G[j] = min(G[j - X[i]], F[i - 1][j - X[i]]) + 1;if (!H[i] || j > L[i] && j < H[i]){F[i][j] = G[j];if (j + Y[i] <= M) F[i][j] = min(F[i][j], F[i - 1][j + Y[i]]);}}if (!H[i])for (int j = 1; j <= M; j ++)F[i][M] = min(F[i][M], F[i - 1][j] + max(1ll, (M - j + X[i] - 1) / X[i]));}int Result = INF;for (int j = 1; j <= M; j ++)Result = min(Result, F[N][j]);if (Result < INF)cout << 1 << endl << Result << endl;else{cout << 0 << endl;for (int i = N; i >= 0; i --){bool Flag = false;for (int j = 1; j <= M; j ++)if (F[i][j] < INF){int Count = 0;for (int k = 0; k <= i; k ++)if (H[k])Count ++;cout << Count << endl;Flag = true;break;}if (Flag) break;}}return 0;
}