题目

给定 n 个区间 [ai,bi] 和 n 个整数 ci。

你需要构造一个整数集合 Z，使得 ∀i∈[1,n]，Z 中满足 ai≤x≤bi 的整数 x 不少于 ci 个。

求这样的整数集合 Z 最少包含多少个数。

输入格式

第一行包含整数 n。

接下来 n 行，每行包含三个整数 ai,bi,ci。

输出格式

输出一个整数表示结果。

数据范围

1 ≤ n ≤ 50000
0 ≤ ai,bi ≤ 50000
0 ≤ ci ≤ bi − ai + 1

输入样例：

5
3 7 3
8 10 3
6 8 1
1 3 1
10 11 1

输出样例：

6

思路

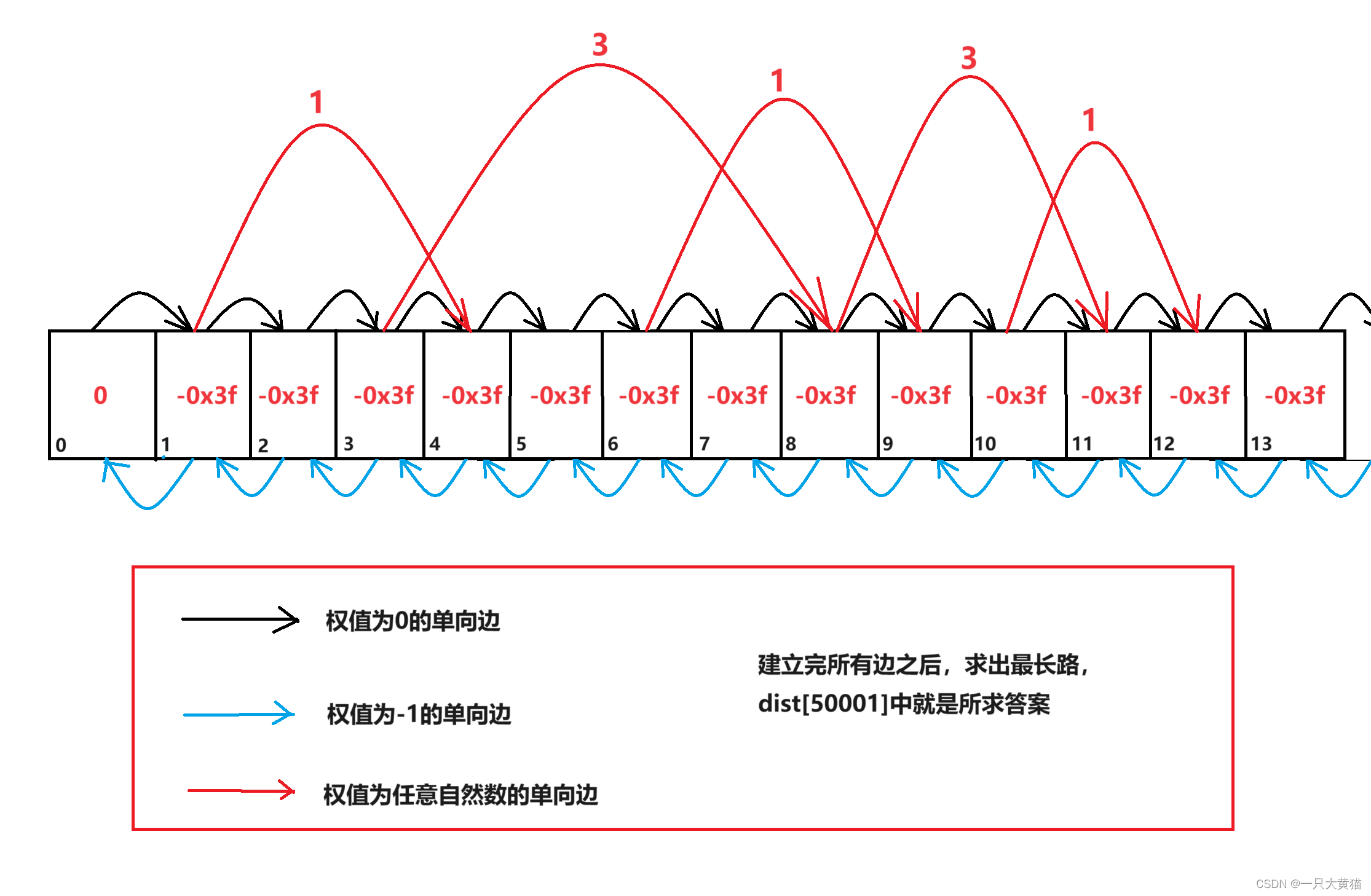
按照样例，我们可以得到一张图。

 差分约束：

（1）求不等式组的可行解

                源点需要满足条件：从原点出发，一定可以走到所有边。

步骤：

【1】先将每个不等式 xi <= xj + ck，转化为一条从xj走到xi的，长度为ck的一条边。

【2】找一个超级源点，使得该源点一定可以遍历到所有的边。

【3】从源点求一遍单源最短路

        结果1：如果存在负环，则原不等式组一定无解。

        结果2：如果没有负环，则dist[ i ]就是原不等式组的一个可行解。

（2）如何求最大值或者最小值，这里的最值指的是每个变量的最值

        结论：如果求的是最小值，则应该是求最长路；如果求的是最大值，则应该是求最短路。

        问题：如何转化x1 <= c，其中一个是常数这类不等式。

        方法：建立一个超级源点，然后建立0 -> i，长度是c的边即可。

代码 

#include<bits/stdc++.h>
using namespace std;
const int N = 200000;
int n;
int h[N],e[N],ne[N],w[N],idx;
int dist[N];
bool st[N];void add(int a,int b,int c)
{ne[idx] = h[a],e[idx] = b,w[idx] = c,h[a] = idx ++;
}void spfa()
{queue<int> q;dist[0] = 0;q.push(0);st[0] = true;while(!q.empty()){int t = q.front();q.pop();st[t] = false;for(int i = h[t]; ~i ; i = ne[i]){int j = e[i];if(dist[j] < dist[t] + w[i]){dist[j] = dist[t] + w[i];if(!st[j]){st[j] = true;q.push(j);}}}}
}int main()
{memset(dist,-0x3f,sizeof dist);memset(h,-1,sizeof h);cin >> n;for(int i = 1; i <= 50001; i ++){add(i-1,i,0);add(i,i-1,-1);}for(int i = 1; i <= n; i ++){int a,b,c;cin >> a >> b >> c;add(a,b + 1,c);}spfa();cout << dist[50001] << endl;return 0;
}

题目来自：https://www.acwing.com/