文章目录
- 0 代码仓库
- 1 Dijkstra算法
- 2 Dijkstra算法的实现
- 2.1 设置距离数组
- 2.2 找到当前路径的最小值 curdis,及对应的该顶点cur
- 2.3 更新权重
- 2.4 其他接口
- 2.4.1 判断某个顶点的连通性
- 2.4.2 求源点s到某个顶点的最短路径
- 3使用优先队列优化-Dijkstra算法
- 3.1 设计内部类node
- 3.2 入队
- 3.3 记录路径
- 3.4 整体
- 4 Bellman-Ford算法
- 4.1 松弛操作
- 4.2 负权环
- 4.3 算法思想
- 4.4 进行V-1次松弛操作
- 4.5 判断负权环
- 4.6 整体
- 5 Floyed算法
- 5.1 设置记录两点最短距离的数组,并初始化两点之间的距离
- 5.2 更新两点之间的距离
0 代码仓库
https://github.com/Chufeng-Jiang/Graph-Theory/tree/main/src/Chapter11_Min_Path
1 Dijkstra算法
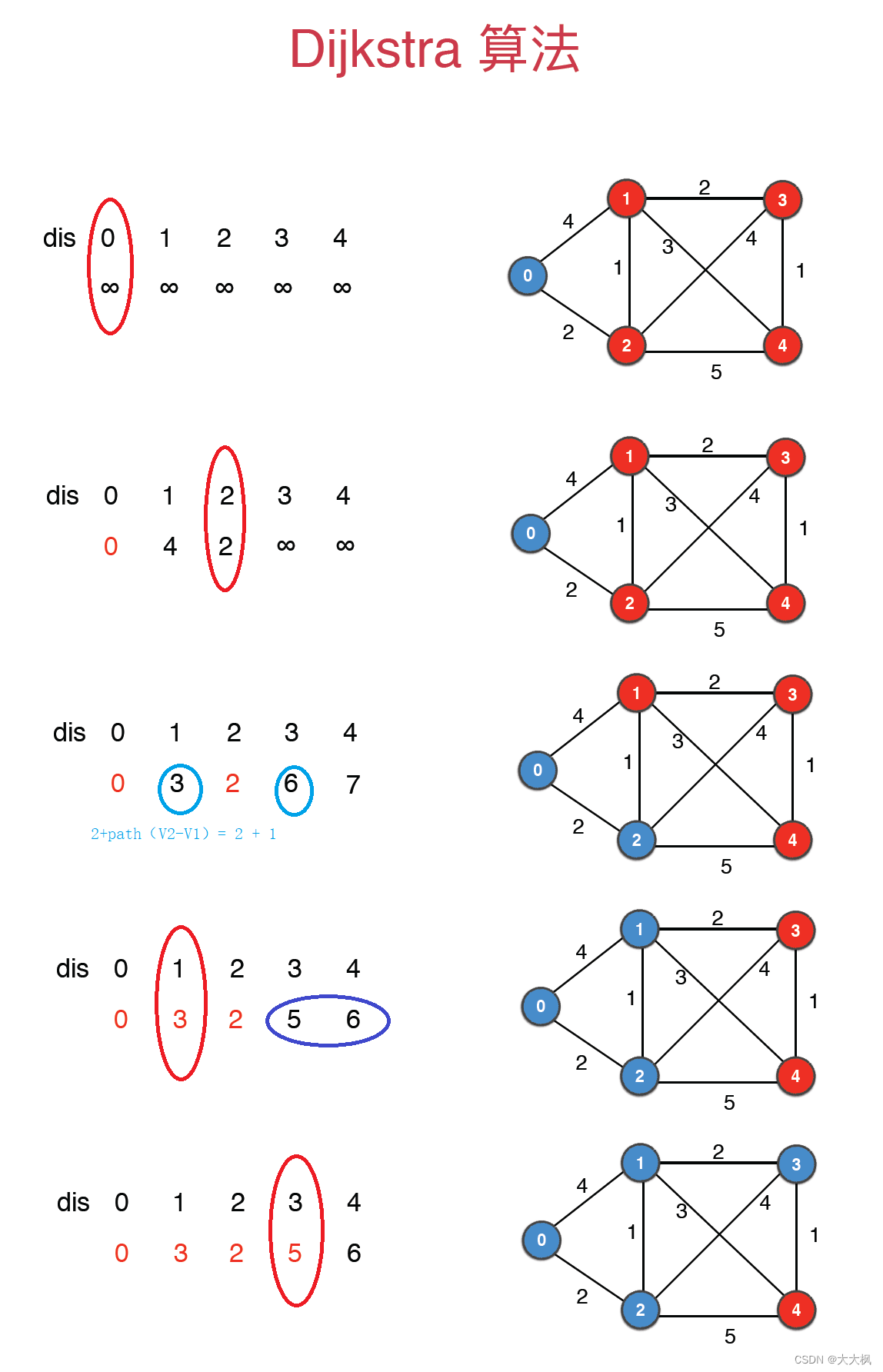
2 Dijkstra算法的实现
2.1 设置距离数组
//用于存储从源点到当前节点的距离,并初始化
dis = new int[G.V()];
Arrays.fill(dis, Integer.MAX_VALUE);
dis[s] = 0;
2.2 找到当前路径的最小值 curdis,及对应的该顶点cur
int cur = -1, curdis = Integer.MAX_VALUE;for(int v = 0; v < G.V(); v ++)if(!visited[v] && dis[v] < curdis){curdis = dis[v];cur = v;}
2.3 更新权重
visited[cur] = true;
for(int w: G.adj(cur))if(!visited[w]){if(dis[cur] + G.getWeight(cur, w) < dis[w])dis[w] = dis[cur] + G.getWeight(cur, w);}
2.4 其他接口
2.4.1 判断某个顶点的连通性
public boolean isConnectedTo(int v){G.validateVertex(v);return visited[v];
}
2.4.2 求源点s到某个顶点的最短路径
public int distTo(int v){G.validateVertex(v);return dis[v];
}
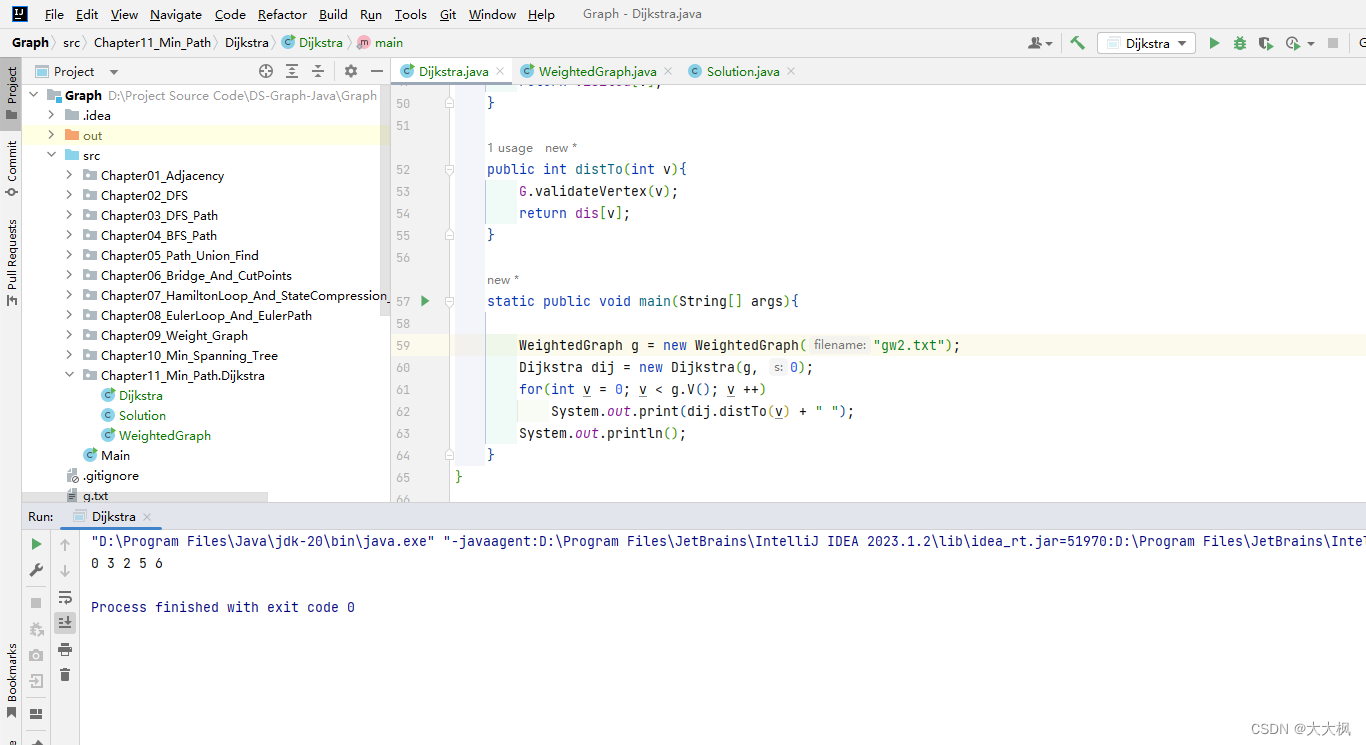
3使用优先队列优化-Dijkstra算法
3.1 设计内部类node
存放节点编号和距离
private class Node implements Comparable<Node>{public int v, dis;public Node(int v, int dis){this.v = v;this.dis = dis;}@Overridepublic int compareTo(Node another){return dis - another.dis;}}
3.2 入队
PriorityQueue<Node> pq = new PriorityQueue<Node>();pq.add(new Node(s, 0));
这里的缺点就是,更新node时候,会重复添加节点相同的node,但是路径值不一样。不影响最后结果。
while(!pq.isEmpty()){int cur = pq.remove().v;if(visited[cur]) continue;visited[cur] = true;for(int w: G.adj(cur))if(!visited[w]){if(dis[cur] + G.getWeight(cur, w) < dis[w]){dis[w] = dis[cur] + G.getWeight(cur, w);pq.add(new Node(w, dis[w]));pre[w] = cur;}}
}
3.3 记录路径
private int[] pre;
- 更新pre数组
for(int w: G.adj(cur))if(!visited[w]){if(dis[cur] + G.getWeight(cur, w) < dis[w]){dis[w] = dis[cur] + G.getWeight(cur, w);pq.add(new Node(w, dis[w]));pre[w] = cur;}}
- 输出路径
public Iterable<Integer> path(int t){ArrayList<Integer> res = new ArrayList<>();if(!isConnectedTo(t)) return res;int cur = t;while(cur != s){res.add(cur);cur = pre[cur];}res.add(s);Collections.reverse(res);return res;}
3.4 整体
package Chapter11_Min_Path.Dijkstra_pq;import java.util.ArrayList;
import java.util.Arrays;
import java.util.Collections;
import java.util.PriorityQueue;public class Dijkstra {private WeightedGraph G;private int s;private int[] dis;private boolean[] visited;private int[] pre;private class Node implements Comparable<Node>{public int v, dis;public Node(int v, int dis){this.v = v;this.dis = dis;}@Overridepublic int compareTo(Node another){return dis - another.dis;}}public Dijkstra(WeightedGraph G, int s){this.G = G;G.validateVertex(s);this.s = s;dis = new int[G.V()];Arrays.fill(dis, Integer.MAX_VALUE);pre = new int[G.V()];Arrays.fill(pre, -1);dis[s] = 0;pre[s] = s;visited = new boolean[G.V()];PriorityQueue<Node> pq = new PriorityQueue<Node>();pq.add(new Node(s, 0));while(!pq.isEmpty()){int cur = pq.remove().v;if(visited[cur]) continue;visited[cur] = true;for(int w: G.adj(cur))if(!visited[w]){if(dis[cur] + G.getWeight(cur, w) < dis[w]){dis[w] = dis[cur] + G.getWeight(cur, w);pq.add(new Node(w, dis[w]));pre[w] = cur;}}}}public boolean isConnectedTo(int v){G.validateVertex(v);return visited[v];}public int distTo(int v){G.validateVertex(v);return dis[v];}public Iterable<Integer> path(int t){ArrayList<Integer> res = new ArrayList<>();if(!isConnectedTo(t)) return res;int cur = t;while(cur != s){res.add(cur);cur = pre[cur];}res.add(s);Collections.reverse(res);return res;}static public void main(String[] args){WeightedGraph g = new WeightedGraph("g.txt");Dijkstra dij = new Dijkstra(g, 0);for(int v = 0; v < g.V(); v ++)System.out.print(dij.distTo(v) + " ");System.out.println();System.out.println(dij.path(3));}
}4 Bellman-Ford算法
4.1 松弛操作
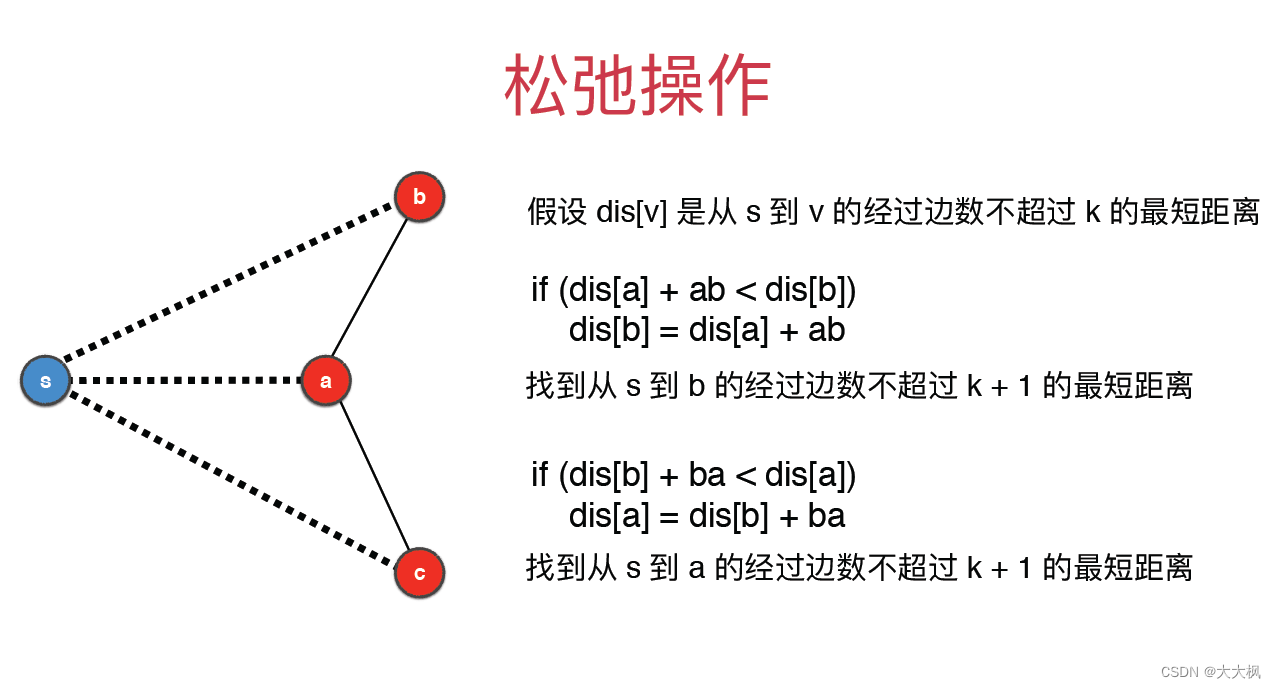
4.2 负权环
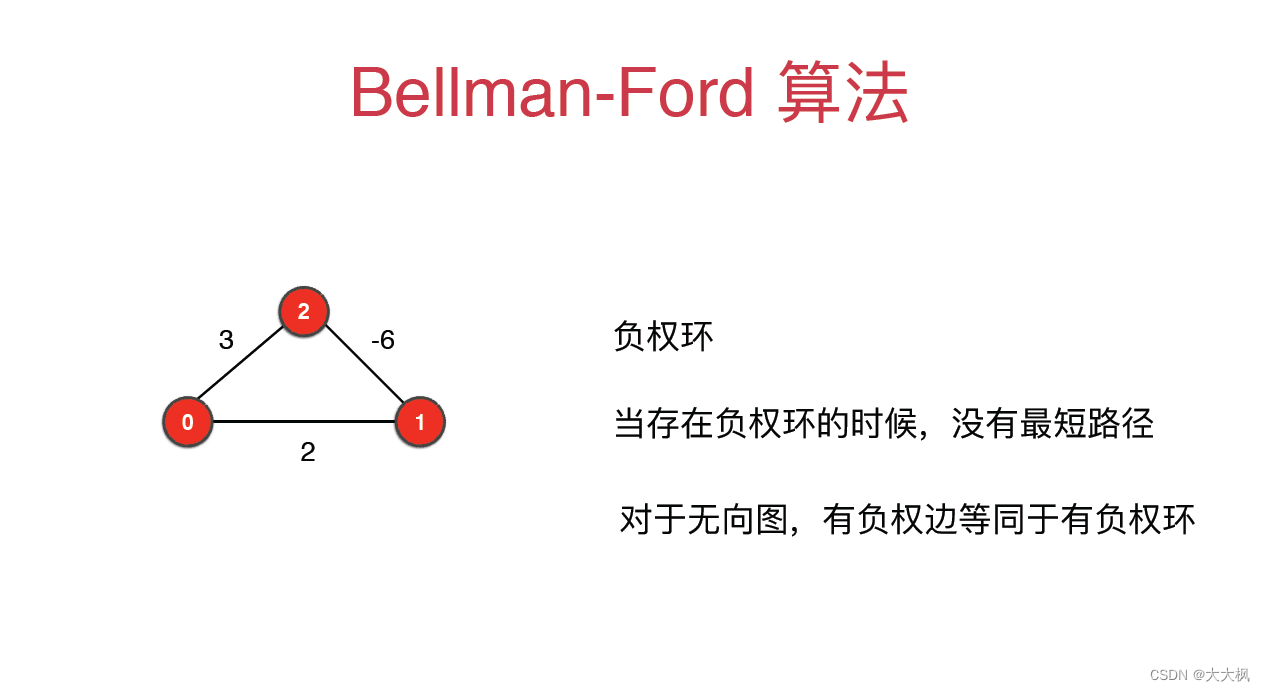
4.3 算法思想

4.4 进行V-1次松弛操作
// 进行V-1次松弛操作
for(int pass = 1; pass < G.V(); pass ++){for(int v = 0; v < G.V(); v ++)for(int w: G.adj(v))if(dis[v] != Integer.MAX_VALUE && // 避免对无穷值的点进行松弛操作dis[v] + G.getWeight(v, w) < dis[w]){dis[w] = dis[v] + G.getWeight(v, w);pre[w] = v;}
}
4.5 判断负权环
// 多进行一次操作,如果还有更新,那么存在负权换
for(int v = 0; v < G.V(); v ++)for(int w : G.adj(v))if(dis[v] != Integer.MAX_VALUE &&dis[v] + G.getWeight(v, w) < dis[w])hasNegCycle = true;
4.6 整体
package Chapter11_Min_Path.BellmanFord;import java.util.ArrayList;
import java.util.Arrays;
import java.util.Collections;public class BellmanFord {private WeightedGraph G;private int s;private int[] dis;private int[] pre;private boolean hasNegCycle = false;public BellmanFord(WeightedGraph G, int s){this.G = G;G.validateVertex(s);this.s = s;dis = new int[G.V()];Arrays.fill(dis, Integer.MAX_VALUE);dis[s] = 0;pre = new int[G.V()];Arrays.fill(pre, -1);// 进行V-1次松弛操作for(int pass = 1; pass < G.V(); pass ++){for(int v = 0; v < G.V(); v ++)for(int w: G.adj(v))if(dis[v] != Integer.MAX_VALUE && // 避免对无穷值的点进行松弛操作dis[v] + G.getWeight(v, w) < dis[w]){dis[w] = dis[v] + G.getWeight(v, w);pre[w] = v;}}// 多进行一次操作,如果还有更新,那么存在负权换for(int v = 0; v < G.V(); v ++)for(int w : G.adj(v))if(dis[v] != Integer.MAX_VALUE &&dis[v] + G.getWeight(v, w) < dis[w])hasNegCycle = true;}public boolean hasNegativeCycle(){return hasNegCycle;}public boolean isConnectedTo(int v){G.validateVertex(v);return dis[v] != Integer.MAX_VALUE;}public int distTo(int v){G.validateVertex(v);if(hasNegCycle) throw new RuntimeException("exist negative cycle.");return dis[v];}public Iterable<Integer> path(int t){ArrayList<Integer> res = new ArrayList<Integer>();if(!isConnectedTo(t)) return res;int cur = t;while(cur != s){res.add(cur);cur = pre[cur];}res.add(s);Collections.reverse(res);return res;}static public void main(String[] args){WeightedGraph g = new WeightedGraph("gw2.txt");BellmanFord bf = new BellmanFord(g, 0);if(!bf.hasNegativeCycle()){for(int v = 0; v < g.V(); v ++)System.out.print(bf.distTo(v) + " ");System.out.println();System.out.println(bf.path(3));}elseSystem.out.println("exist negative cycle.");WeightedGraph g2 = new WeightedGraph("g2.txt");BellmanFord bf2 = new BellmanFord(g2, 0);if(!bf2.hasNegativeCycle()){for(int v = 0; v < g2.V(); v ++)System.out.print(bf2.distTo(v) + " ");System.out.println();}elseSystem.out.println("exist negative cycle.");}
}5 Floyed算法

5.1 设置记录两点最短距离的数组,并初始化两点之间的距离
private int[][] dis;
- 初始化两点之间的距离
for(int v = 0; v < G.V(); v ++){dis[v][v] = 0;for(int w: G.adj(v))dis[v][w] = G.getWeight(v, w);
}
5.2 更新两点之间的距离
第一重循环:测试两点之间经过点t是否存在更短的路径。
for(int t = 0; t < G.V(); t ++)for(int v = 0; v < G.V(); v ++)for(int w = 0; w < G.V(); w ++)if(dis[v][t] != Integer.MAX_VALUE && dis[t][w] != Integer.MAX_VALUE&& dis[v][t] + dis[t][w] < dis[v][w])dis[v][w] = dis[v][t] + dis[t][w];