【每日一题】区域和检索

文章目录

Tag
题目来源
解题思路
- 方法一：分块
- 方法二：线段树
- 方法三：树状数组
写在最后

Tag

【树状数组】【线段树】【分块】【前缀和】【设计类】【2023-11-13】

题目来源

307. 区域和检索 - 数组可修改

解题思路

使用前缀和解决不行吗？

前缀和超时，设计类的题目时间复杂度如何分析？我认为是各个部分调用次数乘上部分代码的时间复杂度。

本题中，初始化的时间复杂度为 $O (n)$ ， $n$ 为数组 nums 的长度，调用类一次就初始化一次。update 的时间复杂度为 $O (mn)$ ， $m$ 为 update 的调用次数。sumRange 的时间复杂度为 $O (k)$ ， $k$ 为 sumRange 的调用次数。因此，前缀和方法总的时间复杂度为 $O (n) + O (mn) + O (kn)$ ，按照题目中的最大数据量来计算总的执行次数达到 $\times10^8$ 接近 $10^9$ ，力扣设置的执行次数上限约为 $10^8$ ，所以前缀和方法超时。

官方题解中给出了两种方法：

分块；
线段树。

接下来具体看一看这两种方法。

方法一：分块

首先根据官方题解中的复杂度分析来看一下分块方法总的时间复杂度：

$\sqrt{n})$

其中， $n$ 为数组 nums 的长度， $m$ 为 update 的调用次数， $k$ 为 sumRange 的调用次数。总的数据规模（执行次数）达到 $10^6$ ，不会超时。

接下来就跟着官方题解来学习一下分块思想的解决方法。

将数组 nums 分成多个块，每个块的大小为 size， $\sqrt{n}$ ， $n$ 为数组 nums 的长度。维护一个数组 sum 来保存每个块中的元素和。

构造函数：
计算块 size 的大小，并初始化 sum。
update 函数
根据下标 idx 更新数组 nums 以及数组 sum。
sumRange 函数
首先计算出 left 所在的块 b1，right 所在的块 b2 以及 left 和 right 在对应块中的索引 i1 和 i2：
- 如果 b1 = b2，那么直接返回 b1 块中区间 [i1, i2] 中的元素和；
- 否则分三部分计算区间 [left, right] 中的和，第一部分是 b1 块中区间 [i1, size-1] 的元素和 sum1，第二部分是 b2 块中区间 [0, i2] 的元素和 sum2，第三部分是块区间 [b1+1, b2-1] 中的元素总和，此时返回 sum1 + sum2 + sum3。

实现代码

class NumArray {
private:int size;   // 块大小vector<int> sum;vector<int>& nums;
public:NumArray(vector<int>& nums): nums(nums) {int n = nums.size();size = sqrt(n);sum.resize((n + size - 1) / size);for (int i  = 0; i < n; ++i) {sum[i / size] += nums[i];}}void update(int idx, int val) {sum[idx / size] += val - nums[idx];nums[idx] = val;}int sumRange(int left, int right) {int b1 = left / size, b2 = right / size;int i1 = left % size, i2 = right % size;// 情况一if (b1 == b2) {return accumulate(nums.begin() + b1*size + i1, nums.begin() + b1*size + i2 + 1, 0);}int sum1 = accumulate(nums.begin() + b1 * size + i1, nums.begin() + b1 * size + size, 0);int sum2 = accumulate(nums.begin() + b2 * size, nums.begin() + b2 * size + i2 + 1, 0);int sum3 = accumulate(sum.begin() + b1 + 1, sum.begin() + b2, 0);return sum1 + sum2 + sum3;}
};/*** Your NumArray object will be instantiated and called as such:* NumArray* obj = new NumArray(nums);* obj->update(index,val);* int param_2 = obj->sumRange(left,right);*/

复杂度分析

时间复杂度：构造函数的时间复杂度为 $O (n)$ ，update 函数的时间复杂度为 $O (1)$ ，sumRange 函数的时间复杂度为 $O (n)$ 。对于 sumRange 函数，我们最多遍历两个块以及 sum 数组，因此时间复杂度为 $\times 10 + \sqrt{n}$ ，渐进时间复杂度为 $O(\sqrt{n})$ 。

空间复杂度： $O(\sqrt{n})$ ，因为数组 sum 需要 $O(\sqrt{n})$ 的空间。

方法二：线段树

线段树的每个节点可以保存数组 nums 在区间 [s, e] 上的最小值、最大值或者总和的信息。本题正好是有关数组区间和的问题，可以使用线段树来解决。

线段树可以使用数组来实现。具体地，根节点的为 0，对应的是数组 nums 中所有元素的和；如果某一个节点在数组中的下标为 node，那么它的左子节点下标为 node * 2 + 1，右子节点下标为 node * 2 + 2。

本题中的线段树需要以下几种方法：

建树的 build 函数
在节点 node 中保存数组 nums 在区间 [s, e] 的总和：
- s = e 时，节点 node 是叶子节点，它保存的值为 nums[s]；
- s < e 时，节点 ndoe 的左子结点保存的是区间 $\lfloor{\frac{s+e}{2}\rfloor}]$ 的总和，右子节点保存的是区间 $[\lfloor{\frac{s+e}{2}\rfloor} + 1, e]$ 的总和，节点 node 保存的值就等于它的两个子节点保存的值之和。
单点修改 change 的函数
当我们需要修改 nums[idx] 的值时，我们找到对应区间 [idx, idx] 的叶子节点，直接修改叶子节点的值为 val，然后自下而上递归地更新父节点的值。
范围求和 range 函数
给定区间 [left, right] 时，我们将区间 [left, right] 拆分成多个节点对应的区间：
- 如果 node 对应的区间与 [left, right] 相同，可以直接返回该节点的值；
- 否则，我们从根节点开始递归地拆分区间计算 [left, right] 范围和。

实现代码

class NumArray {
private:vector<int> segmentTree;int n;// 节点node是segmentTree数组中的下标，下标对应的值为nums数组中区间[s, e]的元素和void build(int node, int s, int e, vector<int>& nums) {if (s == e) {segmentTree[node] = nums[s];return;}int m = s + (e - s) / 2;build(node * 2 + 1, s, m, nums);build(node * 2 + 2, m + 1, e, nums);segmentTree[node] = segmentTree[node * 2 + 1] + segmentTree[node * 2 + 2];}// 找到idx对应的叶子结点更改叶子节点的值，自下而上更改线段树void change(int idx, int val, int node, int s, int e) {if (s == e) {segmentTree[node] = val;return;}int m = s + (e - s) / 2;if (idx <= m) {change(idx, val, node * 2 + 1, s, m);}else {change(idx, val, node * 2 + 2, m+1, e);}segmentTree[node] = segmentTree[node * 2 + 1] + segmentTree[node * 2 + 2];}// 自上而下锁定区间int range(int left, int right, int node, int s, int e) {if (left == s && right == e) {return segmentTree[node];}int m = s + (e - s) / 2;if (right <= m) {return range(left, right, node * 2 + 1, s, m);}else if (left > m) {return range(left, right, node * 2 + 2, m + 1, e);}else {return range(left, m, node * 2 + 1, s, m) + range(m+1, right, node * 2 + 2, m+1, e);}}public:NumArray(vector<int>& nums): n(nums.size()), segmentTree(nums.size() * 4) {build(0, 0, n-1, nums);}void update(int index, int val) {change(index, val, 0, 0, n-1);}int sumRange(int left, int right) {return range(left, right, 0, 0, n-1);}
};/*** Your NumArray object will be instantiated and called as such:* NumArray* obj = new NumArray(nums);* obj->update(index,val);* int param_2 = obj->sumRange(left,right);*/

复杂度分析

时间复杂度：构造函数时间复杂度为 $O (n)$ ，update 函数时间复杂度为 $O (l o g n)$ ，sumRange 函数的时间复杂度为 $O (l o g n)$ 。根据本题的数据量，最大数据规模（执行次数）为 $10^5$ 。

空间复杂度： $O (n)$ ，保存 setmentTree 需要的空间。

方法三：树状数组

初学树状数组，试着来分析一下树状数组的原理与使用。

首先，先来看一个位运算的代码：

int lowBit(int x) {return x & -x
}

WTF? 这是在干啥，我们来一点点分析。在不理解某一段代码是用来干啥的时候，最好的办法是找几个数带入代码，顺着代码走走人为执行一下，看看最后会输出什么。我们把 x = 6 带入函数中执行看一看。

进行与运算，我们要先把整型数字 6 装化成二进制数，计算机中存储的是补码，正数的原码、反码、补码都是一样的，8 位二进制位 0000 0110；-6 的原码为 1000 0110（最高位的 1 表示负数），反码为 1111 1001，补码为反码 +1 即为1111 1010；6 & (-6) = 0000 0010 对应的整型数字为 2。再举几个例子就会发现 x & (-x) 计算得到的 x 对应二进制数的最低位的 1 所在的位置。

在树状数组中就是移动 lowBit 函数来找节点 x 对应的父节点。树状数组（Fenwick Tree）是一种用于维护前缀和的数据结构，主要用于快速计算数组区间的和。它的主要优势在于更新和查询操作的时间复杂度都是 $O (l o g N)$ ，其中 $N$ 是数组的大小。

树状数组维护的是累加和数组 tree，如图 1 所示（树状数组题解中的所有图均来自 [树状数组] 详解树状数组, 包含更新查询图解, 秒懂lowbit含义(JAVA 65ms, 68.6MB)），经过 add 函数之后，tree 数组在结构上是一种形如 “树” 的结构。通过维护的累计和数组 tree，我们就可以查询任意区间的元素和。

图1

add 函数

add 函数是一种类似于树自下而上的更新 tree 的操作，其实现代码为：

void add(int index, int val) {while (index < tree.size()) {tree[index] += val;index += lowBit(index);}}

比如现在有一个数组 nums 长度为 8，先将 nums[0] 记为 n1 更新到 tree[1] 中，并更新到 tree[x + lowBit(x)] 中，如图 2 3 4 所示将数组 nums 中的值加到 tree 中，时间复杂度为 $O (n l o g n)$ ， $n$ 为数组 nums 的长度。

图 2

图 3

图 4

查询函数

查询树状数组使使用 x -= lowBit(x) 来寻找小于 x 的下一个区间，如图 5 所示：

图 5

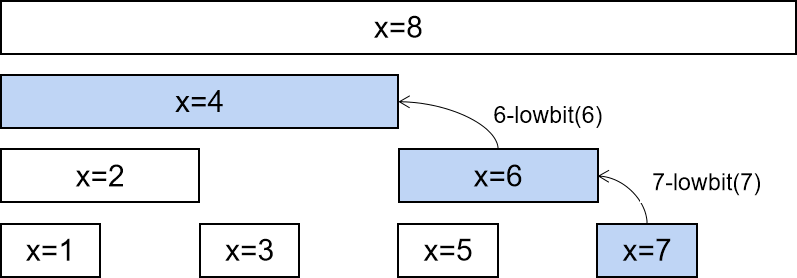
本题可以使用树状数组解决的一个重要的原因是可以使用树状数组中的 add 函数来修改区间，时间复杂度为 $O (l o g n)$ 。

实现代码

class NumArray {
private:vector<int> tree;vector<int>& nums;int lowBit(int x) {return x & -x;}void add(int idx, int val) {while (idx < tree.size()) {tree[idx] += val;idx += lowBit(idx);}}int prefixSum(int idx) {int sum = 0;while (idx > 0) {sum += tree[idx];idx -= lowBit(idx);}return sum;}public:NumArray(vector<int>& nums) : nums(nums), tree(nums.size() + 1) {for (int i = 0; i < nums.size(); ++i) {add(i+1, nums[i]);}}void update(int idx, int val) {add(idx + 1, val - nums[idx]);nums[idx] = val;}int sumRange(int left, int right) {return prefixSum(right + 1) - prefixSum(left);}
};/*** Your NumArray object will be instantiated and called as such:* NumArray* obj = new NumArray(nums);* obj->update(index,val);* int param_2 = obj->sumRange(left,right);*/

复杂度分析

时间复杂度：构造函数的时间复杂度为 $O (n l o g n)$ ， $n$ 是数组 nums 的大小，因为 add 函数的时间复杂度为 $O (l o g n)$ ，需要调用 add $n$ 次。update 函数的时间复杂度为 $O (l o g n)$ ，因为调用了一次 add 函数。sumRange 函数的时间复杂度为 $O (l o g n)$ ，因为调用了两次时间复杂度为 $O (l o g n)$ 的 prefixSum 函数。根据本题的数据量，最大数据规模（执行次数）为 $10^5$ 。