【混合本质】
如果了解骨骼动画就知道,某一时刻角色的Pose是通过两个邻近关键帧依次对所有骨骼插值而来,换句话说就是由两个关键帧混合而来。
那么可不可以由多个关键帧混合而来呢?当然可以。
更多的关键帧可以来自不同的动画片段(AnimationClip),混合时给予每个动画片段的权重不同,但权重之和仍然为1。
我们可以预先指定混合时需要哪些动画片段,通过混合算法在运行时计算每个动画片段的权重。
通过混合可以用有限个动画片段混合出多种角色状态,进而减少动画片段的制作。
混合一般用于角色运动locomotion。
【一维线性插值混合】
一维线性插值混合要求不同动画片段只有一个属性不同,例如角色运动的速度和朝向不同。
以速度为例,有五个动画片段,速度分别是1 2 3 4 5m/s,将不同动画片段按照属性的大小从左到右排成一行。
那么该BlendTree有五个AnimationClip,记录了每个AnimationClip的属性,自身有一个属性参数speed。
运行时角色的运动速度会变化,角色速度的值即为该BlendTree的Speed属性当前的值。
可以从五个AnimationClip中找到当前速度邻近的两个,这样就找到了运行时需要参与混合的动画片段。
(注意,当前速度小于动画片段的最小值,或者大于最大值,那么邻近的动画片段只有1个了,不用混合了)
接下来需要确定两个动画片段的权重分别是多少。显然根据两个动画片段的速度值和当前的速度值,可以确定不同动画的权重。(如何这里看不懂怎么确定的,请先了解下线性插值)
【二维双线性插值混合】
双线性插值需要四个点,Q11、Q21、Q12、Q22。
有一个插值系数a1,让Q11和Q21完成线性插值得到R1,Q12和Q22同样用a2完成线性插值得到R2。
有另一个插值系数a2,让R1和R2完成线性插值得到P

在动画混合中,四个点就表示四个动画片段,X轴和Y轴表示角色运动的两个属性,以速度和朝向为例,a1和a2是运行时根据角色当前的速度和朝向,以及动画片段的属性计算出来的。这个坐标系叫做参数空间parameter space
其中,因为存在公用a1和a2的问题,假设a1对应速度属性,a2对应朝向属性。则要求动画片段Q11和Q12、Q21和Q22相互间速度属性不同,Q11和Q12、Q21和Q22相互间朝向属性不同。
也即,两个属性的两个不同值,对应4个动画片段。
如果两个属性分别由N、M个不同的值,则对应N*M个动画片段。
在实际运行时,需要先根据属性值知道四个动画片段,分两次找,每次找的方式与一维线性插值混合找的方式相同,然后进行双线性插值,得到最后的角色Pose
【二维三角形插值混合】
线性插值是用两个已知点插值计算出一个未知点。当然也可以用三个已知点插值计算出一个未知点。
y = a * y1 + b* y2 + c* y3。一般的,a + b + c = 1.
因此,要计算出插值结果,需要先算出两个未知数a和b。
这恰好可以通过三角形的重心坐标算出:二维坐标系中三个已知点可以组合出来三个向量,向量点乘算出面积,面积之比算出未知数。
在动画混合中,三个点代表三个不同的动画片段,点的坐标是动画片段的属性值。
如果有很多个动画呢?如同二维双线性插值混合中的做法,先找到要参与混合的三个动画片段。
如何找?
我们通常假设在坐标原点附近(最好就是在坐标原点)有一个中心动画片段,这个片段一般为类似Idle的动画片段,叫做中心点。
中心点和所有其他点(也叫采样点)都有一个连线,通过判断运行时传过来的两个属性值构成的点(也叫目标点)位于哪两条连线形成的夹角之间即可。
如何判断?向量叉乘可以判断点在直线的左侧还是右侧。
【更复杂的插值混合】
上述三种混合算法都是比较容易想到、容易理解的算法,真正进行混合时,实际参与混合的动画片段为2或3个。如何希望有更多的动画片段参与混合,那么如何给定每个参数的权重值?
这实质上是一个离散数据插值问题,这里有一个基本假设,假设某个采样点对目标点的影响因子为h,所有采样点影响和为H,那么采样点的权重w = h/H。
注意如果H = 1,那么影响因子就是权重了。
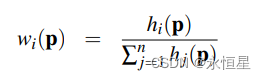
我们只需要找到如何计算影响因子h即可,前面三种简单的方式也是如此,插值方法如下:
- 反距离权重插值Inverse Distance Weighted Interpolation
- 自然邻近插值Natural Neighbors Interpolation
- 径向基函数插值Radial Basis Function Interpolation
- K邻近插值K-Nearest-Neighbors Interpolation
- 梯度带插值Gradient Band Interpolation
【反距离权重插值】
计算所有采样点到目标点的距离,影响因子为距离的倒数 h= 1/distance(s,p)
可以看到距离目标点越近的采样点影响因子越大。
为了减少计算量,可以
1.限制有点的影响距离D,超过该距离,认为不会产生影响
2.不算距离,取距离的平方
【自然邻近插值】
自然邻近插值基于面积(area-based),首先要算出每个采样点的影响面积,采用维诺图算法计算。
随后计算加入目标点后,目标点与周围点形成的维诺图
目标点维诺图和周围点维诺图的重叠面积即为影响因子,如图所示:
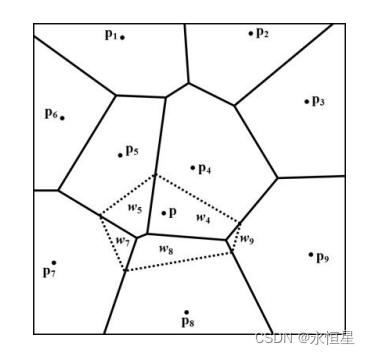
这种方式计算量大,不适合实时计算。
【径向基函数插值】
学过线性代数,我们知道,在向量空间中,任意一个向量都可以用一组基向量的线性组合表示,二维向量空间的基向量个数为2,三维向量空间的基向量个数为3,N维向量空间的基向量个数为N
在函数空间中,任意一个函数都可以用一组基函数的线性组合表示。
径向基函数是取值仅依赖于到原点距离的实值函数。仅依赖表示函数只有一个自变量,为该点到原点的距离,注意原点不是坐标系的原点,原点是我们自己选的。到原点的距离一般指欧式距离,也即我们常用的计算两个点距离的方法。
基本的径向基函数有:

在动画混合中,目标点就是原点,根据其他点到原点的距离以及径向基函数可以计算出来影响因子的值。
【K邻近插值】
类似反距离权重插值,这里只选择距离目标点最近的K个采样点参与实际的混合,第K个采样点的权重为0,更远的采样点的权重也为0。影响因子的计算与反距离权重插值相同。
【梯度带插值】
有三个点O、A、B,在一维线性插值混合中,他们在一条直线上,通过判断O点到A点、O点到B点的距离来计算每个点的影响因子,那么A点和B点的影响因子分别为(此时权重值等于影响因子的值)
h(A) =1 - OA/AB h(B) =1 - OB/AB。
注意如果O在A点左边,那么A的影响因子为1,B的影响因子为0。反之亦然。
如果O点不在AB所在的直线呢?
这时计算距离,要多一个O到AB所在直线的距离。这一项对A点和B点一样,可以抵消掉。我们只要得到O点分别到A点和B点的水平距离即可,用同样的公式可以得到A和B对O的影响。
这个距离如何求?可以看到这实际上是在求向量OA在向量AB上的投影长度。(不知道怎么计算投影长度可以先学习下),随后可以得到h(A)、h(B)
h(A)即为相对于B点,A点对O点的梯度值。如果还有C、D、E点,可以求出相对于这些点,A点对O点的梯度值。
从这些梯度值中,找到最小值,即为在所有采样点中,A点对目标点的影响因子,用公式表示为:
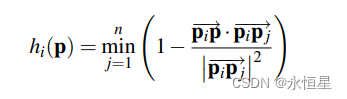
对于已经给定的采样点,如果目标点是未知数,可以计算得到某个采样点关于目标点的梯度值分布(即梯度带),如下图所示:
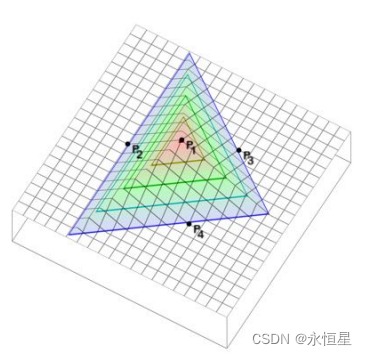
可以看到P1在紫色三角形的顶点附近,仍然存在一定的影响,对含有速度的混合而言,可能不希望受到P1的影响。
这时需要在计算影响因子时考虑角度。角度时目标点P与某个采样点A所在向量的夹角,夹角越小,影响越大。
同样的,如果原点为O,如果点P在直线OA左侧,采样点B在直线OA右侧,那么A点的权重应该为1。
如何综合距离和角度计算影响因子?参考极坐标系的方式,建立一个速度和角度的坐标系,求出目标点和采样点在该坐标系中的位置,再做基于距离的梯度带差值。也即,修改向量的坐标表示方式,如下图所示,其中α是控制因子。
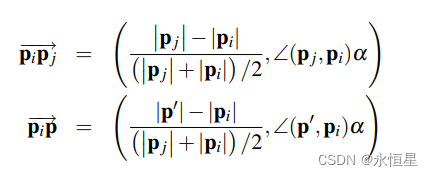
【动画混合中权重算法的评价标准】
- 准确性:如果目标点与某个采样点重合,那么其权重必须为1,其他采样点权重为0。实际上,如果目标点靠近采样点的某个小范围内,那么将目标点和采样带你视为重合。这样做的目的是保留动画师愿意的原始动作。而在回归分析中,会通过统计方法估计出一个最佳的拟合值。
- 累加和:所有权重累加和必须为1
- 连续性:权重函数要具有C0连续性,目标点小的变化只能使权重的变化小,否则会引起混合动作的抖动
- 有界性:所有权重都要在0和1之间,否则会混合出不可预测和不理想的结果
- 局部性:只有目标的附近一定范围内的采样点的权重会大于0,其他采样点的权重为0,这可以提高混合效率。
- 单调性: 每个权重函数应该从其全局最大值递减到全局最小值。严格来说,权重函数不应该有局部最小值。例如,一个奔跑动作的权重应该随着速度从奔跑速度降低到行走速度而从1递减到0。
- 密度不变性:对分布均匀和不均匀的采样点有同样的效果,不应该对附近采样点多的地方比同样邻近的单个采样点更大的权重
【参考】
Unity - Manual: 2D Blending
《游戏引擎架构》
Automated Semi‐Procedural Animation for Character Locomotion





)



)



)


)


