平板光波导中导模的(注意不是泄露模)传播常数β的matlab计算(验证了是对的)

参照的是导波光学_王建(清华大学)的公式(3-1-2、3-1-3)，算的参数是这本书的图3-3的。


function []=PropagationConstantsMain()
clear;clc;close all
lambda0=1.55;%真空或空气中的入射波长，单位um
k0=2*pi/lambda0;
m=3;%导模阶数(需要人为指定)
n1=1.62;%芯区的折射率
n2=1.515;%衬底的折射率
n3=1;%包层的折射率
w=5;%芯区厚度，单位um
TEorTM='TE';%选定极化
beta0=linspace(k0*n2+1e-5,k0*n1-1e-5,500);%导模的传播常数范围(根据公式自动得出)%=================%
Fun=@(x)EigEq(x,k0,n1,n2,n3,m,w,TEorTM);
%=================%figure
y=arrayfun(Fun,beta0);
plot(beta0,y,'ro','MarkerSize',2)
hold on
plot(beta0,zeros(1,length(beta0)),'k--')
hold off
axis tight
xlabel('\beta')if strcmp(TEorTM,'TE')==1%TEtitle('TE')
elseif strcmp(TEorTM,'TM')==1%TMtitle('TM')
endop=fzero(Fun,[beta0(1),beta0(end)]);
disp([TEorTM,'极化下',num2str(m),'阶导模的传播常数为:',num2str(op),'   (注意单位)'])endfunction [oup]=EigEq(beta,k0,n1,n2,n3,m,w,TEorTM)
%beta未知
%m是导模阶数
%w是膜(芯区)厚
k=((k0*n1)^2-beta^2)^(1/2);
P=(beta^2-(k0*n2)^2)^(1/2);
q=(beta^2-(k0*n3)^2)^(1/2);if strcmp(TEorTM,'TE')==1%TEoup=k*w-m*pi-atan(P/k)-atan(q/k);elseif strcmp(TEorTM,'TM')==1%TMoup=k*w-m*pi-atan(P/k*((n1/n2)^2))-atan(q/k*((n1/n3)^2));
endend

做了笔记的PDF图书：https://petmask.lanzoub.com/i9x3W13pnore
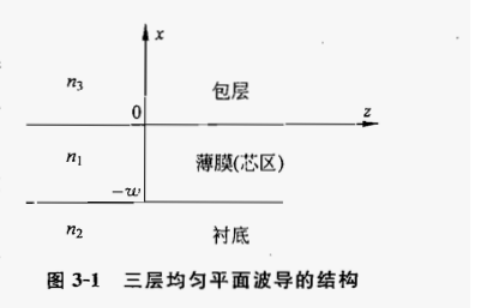
在这里插入图片描述
在这里插入图片描述

注意波导沿着光波传播方向(z向)是无限长的。

Slab waveguide的色散图的计算(未详细验证正确性)


function []=SlabWaveguideDispersionMain()
clear;clc;close all
c_const=299792458;%m/s
lambda0=linspace(0.9,2,1000);%真空或空气中的入射波长范围(人为指定)，单位um
k0=2*pi./lambda0;%行数组
w0=c_const.*k0;%行数组
%m=3;%导模阶数(需要人为指定)
n1=2;%芯区的折射率
n2=1;%衬底的折射率
n3=1;%包层的折射率
w=0.75;%芯区厚度，单位um
TEorTM='TE';%选定极化%============%
figure%限定了导模的范围
plot(w0,n2.*k0,'k--')
hold on
plot(w0,n1.*k0,'k--')
hold on
%============%m0sto=zeros(length(k0),1);%列数组
m1sto=zeros(length(k0),1);%列数组
m2sto=zeros(length(k0),1);%列数组
m3sto=zeros(length(k0),1);%列数组
m4sto=zeros(length(k0),1);%列数组
k0=k0.';%列数组
parfor jj=1:length(k0)Mark=jj/length(k0)K0=k0(jj,1);beta0=linspace(K0*n2+1e-5,K0*n1-1e-5,500).';%导模的传播常数范围(根据公式自动得出)%=================%
m=0;
Fun=@(x)EigEq(x,K0,n1,n2,n3,m,w,TEorTM);
if sign(EigEq(beta0(1),K0,n1,n2,n3,m,w,TEorTM))==sign(EigEq(beta0(end),K0,n1,n2,n3,m,w,TEorTM))m0sto(jj,1)=0;elsem0sto(jj,1)=fzero(Fun,[beta0(1),beta0(end)]);
end
%=================%%=================%
m=1;
Fun=@(x)EigEq(x,K0,n1,n2,n3,m,w,TEorTM);
if sign(EigEq(beta0(1),K0,n1,n2,n3,m,w,TEorTM))==sign(EigEq(beta0(end),K0,n1,n2,n3,m,w,TEorTM))m1sto(jj,1)=0;elsem1sto(jj,1)=fzero(Fun,[beta0(1),beta0(end)]);
end
%=================%%=================%
m=2;
Fun=@(x)EigEq(x,K0,n1,n2,n3,m,w,TEorTM);
if sign(EigEq(beta0(1),K0,n1,n2,n3,m,w,TEorTM))==sign(EigEq(beta0(end),K0,n1,n2,n3,m,w,TEorTM))m2sto(jj,1)=0;elsem2sto(jj,1)=fzero(Fun,[beta0(1),beta0(end)]);
end
%=================%%=================%
m=3;
Fun=@(x)EigEq(x,K0,n1,n2,n3,m,w,TEorTM);
if sign(EigEq(beta0(1),K0,n1,n2,n3,m,w,TEorTM))==sign(EigEq(beta0(end),K0,n1,n2,n3,m,w,TEorTM))m3sto(jj,1)=0;elsem3sto(jj,1)=fzero(Fun,[beta0(1),beta0(end)]);
end
%=================%%=================%
m=4;
Fun=@(x)EigEq(x,K0,n1,n2,n3,m,w,TEorTM);
if sign(EigEq(beta0(1),K0,n1,n2,n3,m,w,TEorTM))==sign(EigEq(beta0(end),K0,n1,n2,n3,m,w,TEorTM))m4sto(jj,1)=0;elsem4sto(jj,1)=fzero(Fun,[beta0(1),beta0(end)]);
end
%=================%endM0=[w0.',m0sto];M0(M0(:,2)==0,:)=[];
M1=[w0.',m1sto];M1(M1(:,2)==0,:)=[];
M2=[w0.',m2sto];M2(M2(:,2)==0,:)=[];
M3=[w0.',m3sto];M3(M3(:,2)==0,:)=[];
M4=[w0.',m4sto];M4(M4(:,2)==0,:)=[];scatter(M0(:,1),M0(:,2),10,'ro');
hold on
scatter(M1(:,1),M1(:,2),10,'ko');
hold on
scatter(M2(:,1),M2(:,2),10,'bo');
hold on
scatter(M3(:,1),M3(:,2),10,'yo');
hold on
scatter(M4(:,1),M4(:,2),10,'kd');
hold off
legend('','','m0','m1','m2','m3','m4')if strcmp(TEorTM,'TE')==1%TEtitle('TE')
elseif strcmp(TEorTM,'TM')==1%TMtitle('TM')
end
xlabel('\omega_{0}')
ylabel('\beta')
axis tight
%disp([TEorTM,'极化下',num2str(m),'阶导模的传播常数为:',num2str(op),'   (注意单位)'])%============%
figure%限定了导模的范围
plot(lambda0,n2.*k0,'k--')
hold on
plot(lambda0,n1.*k0,'k--')
hold on
%============%
M0=[lambda0.',m0sto];M0(M0(:,2)==0,:)=[];
M1=[lambda0.',m1sto];M1(M1(:,2)==0,:)=[];
M2=[lambda0.',m2sto];M2(M2(:,2)==0,:)=[];
M3=[lambda0.',m3sto];M3(M3(:,2)==0,:)=[];
M4=[lambda0.',m4sto];M4(M4(:,2)==0,:)=[];scatter(M0(:,1),M0(:,2),10,'ro');
hold on
scatter(M1(:,1),M1(:,2),10,'ko');
hold on
scatter(M2(:,1),M2(:,2),10,'bo');
hold on
scatter(M3(:,1),M3(:,2),10,'yo');
hold on
scatter(M4(:,1),M4(:,2),10,'kd');
hold off
legend('','','m0','m1','m2','m3','m4')if strcmp(TEorTM,'TE')==1%TEtitle('TE')
elseif strcmp(TEorTM,'TM')==1%TMtitle('TM')
end
xlabel('\lambda_{0}(um)')
ylabel('\beta')
axis tightendfunction [oup]=EigEq(beta,k0,n1,n2,n3,m,w,TEorTM)
%beta未知
%m是导模阶数
%w是膜(芯区)厚
k=((k0*n1)^2-beta^2)^(1/2);
P=(beta^2-(k0*n2)^2)^(1/2);
q=(beta^2-(k0*n3)^2)^(1/2);if strcmp(TEorTM,'TE')==1%TEoup=k*w-m*pi-atan(P/k)-atan(q/k);elseif strcmp(TEorTM,'TM')==1%TMoup=k*w-m*pi-atan(P/k*((n1/n2)^2))-atan(q/k*((n1/n3)^2));
endend

第一个代码加了算有效折射率的


function []=PropagationConstantsMain()
clear;clc;close all
lambda0=9.608016155617717;%真空或空气中的入射波长，单位um
k0=2*pi/lambda0;
m=0;%导模阶数(需要人为指定)
n1=3;%芯区的折射率
n2=1;%衬底的折射率
n3=1;%包层的折射率
w=0.27;%芯区厚度，单位um
TEorTM='TE';%选定极化
beta0=linspace(k0*n2+1e-5,k0*n1-1e-5,500);%导模的传播常数范围(根据公式自动得出)%=================%
Fun=@(x)EigEq(x,k0,n1,n2,n3,m,w,TEorTM);
%=================%figure
y=arrayfun(Fun,beta0);
plot(beta0,y,'ro','MarkerSize',2)
hold on
plot(beta0,zeros(1,length(beta0)),'k--')
hold off
axis tight
xlabel('\beta')if strcmp(TEorTM,'TE')==1%TEtitle('TE')
elseif strcmp(TEorTM,'TM')==1%TMtitle('TM')
endop=fzero(Fun,[beta0(1),beta0(end)]);
disp([TEorTM,'极化下',num2str(m),'阶导模的传播常数为:',num2str(op),'   (注意单位)'])
disp([TEorTM,'极化下',num2str(m),'阶导模的有效折射率为:',num2str(op/k0)])endfunction [oup]=EigEq(beta,k0,n1,n2,n3,m,w,TEorTM)
%beta未知
%m是导模阶数
%w是膜(芯区)厚
k=((k0*n1)^2-beta^2)^(1/2);
P=(beta^2-(k0*n2)^2)^(1/2);
q=(beta^2-(k0*n3)^2)^(1/2);if strcmp(TEorTM,'TE')==1%TEoup=k*w-m*pi-atan(P/k)-atan(q/k);elseif strcmp(TEorTM,'TM')==1%TMoup=k*w-m*pi-atan(P/k*((n1/n2)^2))-atan(q/k*((n1/n3)^2));
endend

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.mzph.cn/news/13925.shtml

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

网络知识点之-路由

网络知识点之-路由

本文章收录至《网络》专栏，点击右上角专栏图标可访问本专栏！ 路由（routing）是指分组从源到目的地时，决定端到端路径的网络范围的进程。路由工作在OSI参考模型第三层——网络层的数据包转发设备。路由器通过转发数据包来…
阅读更多...
MySQL数据库配置及创建用户和授权

MySQL数据库配置及创建用户和授权

注意： 都是基于MySQL8.0以上版本 1、检查是否安装过sql [rootlocalhost ~]# rpm -[qa](https://so.csdn.net/so/search?qqa&spm1001.2101.3001.7020) | grep mysql[rootlocalhost ~]# rpm -qa | grep [mariadb](https://so.csdn.net/so/search?qmariadb&…
阅读更多...
Spark（37）：Streaming DataFrame 和 Streaming DataSet 创建

Spark（37）：Streaming DataFrame 和 Streaming DataSet 创建

目录 0. 相关文章链接 1. 概述 2. socket source 3. file source 3.1. 读取普通文件夹内的文件 3.2. 读取自动分区的文件夹内的文件 4. kafka source 4.1. 导入依赖 4.2. 以 Streaming 模式创建 Kafka 工作流 4.3. 通过 Batch 模式创建 Kafka 工作流 5. Rate Source…
阅读更多...
随笔03 考研笔记整理

随笔03 考研笔记整理

图源：文心一言 上半年的博文整理，下半年依然会更新考研类的文章，有需要的小伙伴看向这里~~🧩🧩 另外，这篇文章可能是我上半年的努力成果之一，因此仅关注博主的小伙伴能够查看它~~&#x1f9e…
阅读更多...
嵌入式系统中的GPIO控制：从理论到实践与高级应用

嵌入式系统中的GPIO控制：从理论到实践与高级应用

本文将探讨嵌入式系统中的GPIO（通用输入输出）控制，着重介绍GPIO的原理和基本用法。我们将使用一个实际的示例项目来演示如何通过编程配置和控制GPIO引脚。将基于ARM Cortex-M微控制器，并使用C语言进行编写。 GPIO是嵌入式系统中最常见且功能最强大的接口之一。它允许硬件工…
阅读更多...
基于RK3588+FPGA+AI算法定制的智慧交通与智能安防解决方案

基于RK3588+FPGA+AI算法定制的智慧交通与智能安防解决方案

随着物联网、大数据、人工智能等技术的快速发展，边缘计算已成为当前信息技术领域的一个热门话题。在物联网领域，边缘计算被广泛应用于智慧交通、智能安防、工业等多个领域。因此，基于边缘计算技术的工业主板设计方案也受到越来越多人的关注。…
阅读更多...
linux 指令 第3期

linux 指令 第3期

cat cat 指令： 首先我们知道一个文件内容属性 我们对文件操作就有两个方面：对文件内容和属性的操作 扩展：echo 指令 直接打印echo后面跟的字符串 看： 这其实是把它打印到了显示器上，我们也可以改变一下它的打印位置…
阅读更多...
网络层中一些零碎且易忘的知识点

网络层中一些零碎且易忘的知识点

异构网络：指传输介质、数据编码方式、链路控制协议以及数据单元格式和转发机制不同，异构即物理层和数据链路层均不同RIP、OSPF、BGP分别是哪一层的协议： -RIPOSPFBGP所属层次应用层网络层应用层封装在什么协议中UDPIPTCP 一个主机可以有多个I…
阅读更多...
Bootloader

Bootloader

Bootloader 一段有下载和引导功能的程序 下载应用程序引导使MCU运行在应用程序中，只在有更新请求或者APP无效的时候才会激活 APP和Bootloader都存在Flash中Flash Driver用来擦除APP，下载临时存放在RAM中，下载完成后复位释放。一般随用随下&a…
阅读更多...
Pytorch个人学习记录总结 玩俄罗斯方块の深度学习小项目

Pytorch个人学习记录总结 玩俄罗斯方块の深度学习小项目

目录 前言 模型成果演示 训练过程演示 代码实现 deep_network tetris test train 前言 当今，深度学习在各个领域展现出了惊人的应用潜力，而游戏开发领域也不例外。俄罗斯方块作为经典的益智游戏，一直以来深受玩家喜爱。在这个项目中&…
阅读更多...
Python web实战 | 用 Flask 框架快速构建 Web 应用【实战】

Python web实战 | 用 Flask 框架快速构建 Web 应用【实战】

概要 Python web 开发已经有了相当长的历史，从最早的 CGI 脚本到现在的全栈 Web 框架，现在已经成为了一种非常流行的方式。 Python 最早被用于 Web 开发是在 1995 年（90年代早期），当时使用 CGI 脚本编写动态 Web 页面…
阅读更多...
spring启动流程 (6完结) springmvc启动流程

spring启动流程 (6完结) springmvc启动流程

SpringMVC的启动入口在SpringServletContainerInitializer类，它是ServletContainerInitializer实现类(Servlet3.0新特性)。在实现方法中使用WebApplicationInitializer创建ApplicationContext、创建注册DispatcherServlet、初始化ApplicationContext等。 SpringMVC…
阅读更多...
68. 文本左右对齐

68. 文本左右对齐

题目链接：力扣 解题思路：遍历单词数组，确定每一行的单词数量， 之后就可以得到每一个需要补充的空格数量。从而得到单词之间需要补充的空格数量。具体算法如下： 确定每一行的单词数量 初始值： num 0&…
阅读更多...
【JavaWeb】正则表达式

【JavaWeb】正则表达式

🎄欢迎来到边境矢梦的csdn博文，本文主要讲解Java 中正则表达式 的相关知识🎄 🌈我是边境矢梦，一个正在为秋招和算法竞赛做准备的学生🌈 🎆喜欢的朋友可以关注一下🫰🫰&am…
阅读更多...
2023年的深度学习入门指南(22) - 百川大模型13B的运行及量化

2023年的深度学习入门指南(22) - 百川大模型13B的运行及量化

2023年的深度学习入门指南(22) - 百川大模型13B的运行及量化 不知道上一讲的大段代码大家看晕了没有。但是如果你仔细看了会发现，其实代码还是不全的。比如分词器我们就没讲。 另外，13B比7B的改进点也没有讲。 再有，对于13B需要多少显存我们…
阅读更多...
ios 查看模拟器沙盒的路径

ios 查看模拟器沙盒的路径

打一个断点运行程序，在xcode consol底部控制台输入： po NSHomeDirectory() 复制路径粘帖到前往文件夹打开沙盒缓存文件夹
阅读更多...
golang pprof

golang pprof

pprof是一个用于分析数据的可视化和分析工具，由谷歌公司的开发团队使用go语言编写成的。一般用于对golang资源占用进行分析。不是原创，参考：https://juejin.cn/post/7122473470424219656 1. 通过页面查看golang运行情况 访问 http://127.0.0…
阅读更多...
ppt怎么压缩到10m以内？分享好用的压缩方法

ppt怎么压缩到10m以内？分享好用的压缩方法

PPT是一种常见的演示文稿格式，有时候文件过大，我们会遇到无法发送、上传的现象，这时候简单的解决方法就是压缩其大小，那怎么才能将PPT压缩到10M以内呢？ PPT文件大小受到影响的主要因素就是以下几点： 1、图…
阅读更多...
Keepalived 在CentOS安装

Keepalived 在CentOS安装

下载 有两种下载方式，一种为yum源下载，另一种通过源代码下载，本文章使用源代码编译下载。 官网下载地址：https://www.keepalived.org/download.html wget https://www.keepalived.org/software/keepalived-2.0.20.tar.gz --no-…
阅读更多...
CNN卷积详解

CNN卷积详解

转载自：https://blog.csdn.net/yilulvxing/article/details/107452153 仅用于自己学习过程中经典文章讲解的记录，防止原文失效。 1：单通道卷积 以单通道卷积为例，输入为（1,5,5），分别表示1个通道…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023