独立集问题：安排互不冲突的个体

四个斜眼枪手

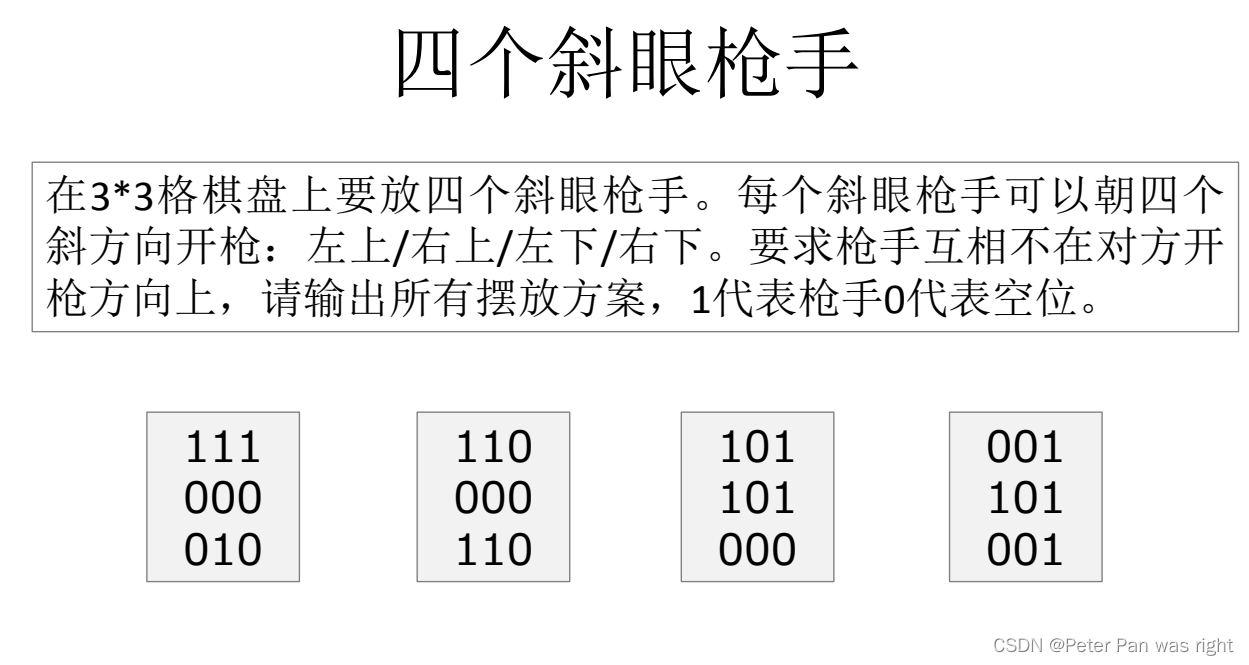
bool valid(int x,int y){for(int i=1;i<=min(x,y);i++)if(f[x-i][y-i]) return 0;for(int i=1;i<=min(x,N-1-y);i++)if(f[x-i][y+i]) return 0;return 1;
}

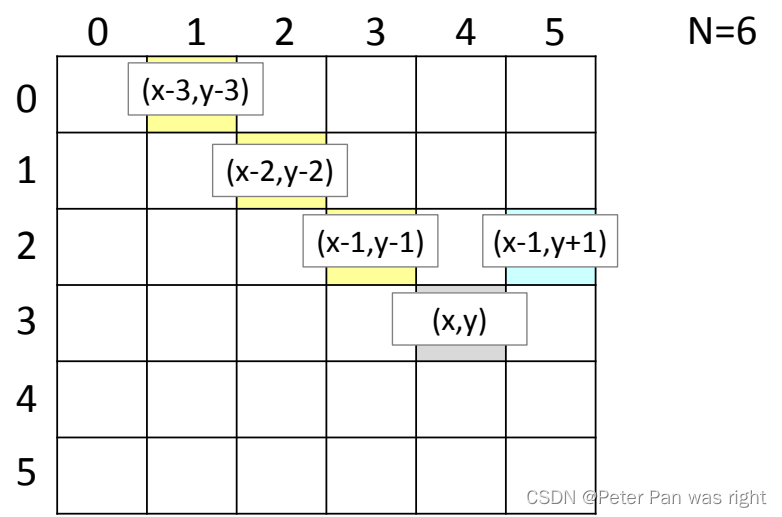
void dfs(int x,int y,int c){if(c==GUNS){ans++;print();return;}if(x==N) return;int nx=(y==N-1?x+1:x);//计算下一格 int ny=(y==N-1?0:y+1);if(valid(x,y)){//判断(x,y)是否能放新的枪手 f[x][y]=1;dfs(nx,ny,c+1);//从(nx,ny)继续枚举，已经放了c+1个枪手 f[x][y]=0;}dfs(nx,ny,c);//(nx,ny)继续枚举，已经放了c个枪手 
}

大家看我注释就看懂了， 此处略去100字……

其实我们可以对他进行剪枝，也就是if((N-1-x)*N+(N-y)+c<=GUNS) return;

八皇后问题

这个问题有两种算法：1、逐格放置 2、逐行放置

逐格放置

和“四个斜眼枪手”差不多

void dfs(int x,int y,int c){if(c==GUNS){ans++;print();return;}if(x==N) return;if((N-1-x)*N+(N-y)+c<=GUNS) return;int nx=(y==N-1?x+1:x);int ny=(y==N-1?0:y+1);if(valid(x,y)){f[x][y]=1;dfs(nx,ny,c+1);f[x][y]=0;}dfs(nx,ny,c);
}

bool valid(int x,int y){for(int i=1;i<=min(x,y);i++)if(f[x-i][y-i]) return 0;for(int i=1;i<=min(x,N-1-y);i++)if(f[x-i][y+i]) return 0;for(int i=0;i<x;i++)if(f[i][y]) return 0;for(int i=0;i<y;i++)if(f[x][i]) return 0;return 1;
}

逐行放置

bool valid(int x,int y){return !clmn[y]&&!d1[x+y]&&!d2[x-y+N-1];
}

为什么呢？我亲自给大家画了三张图，如下

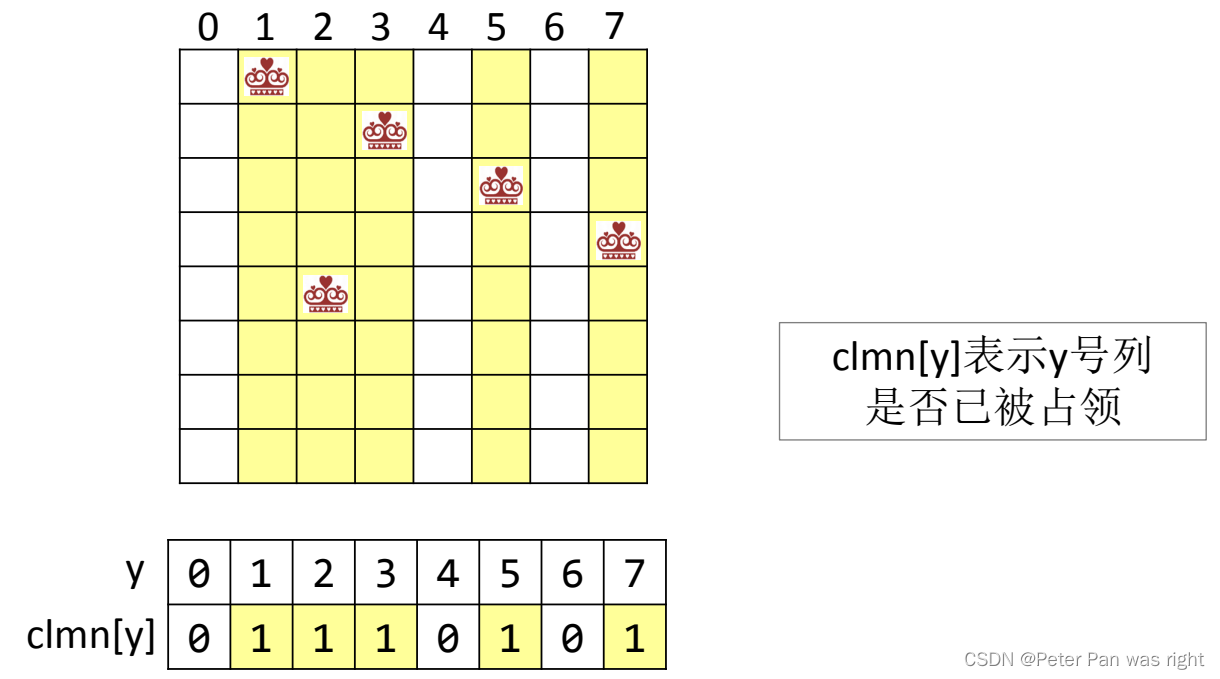
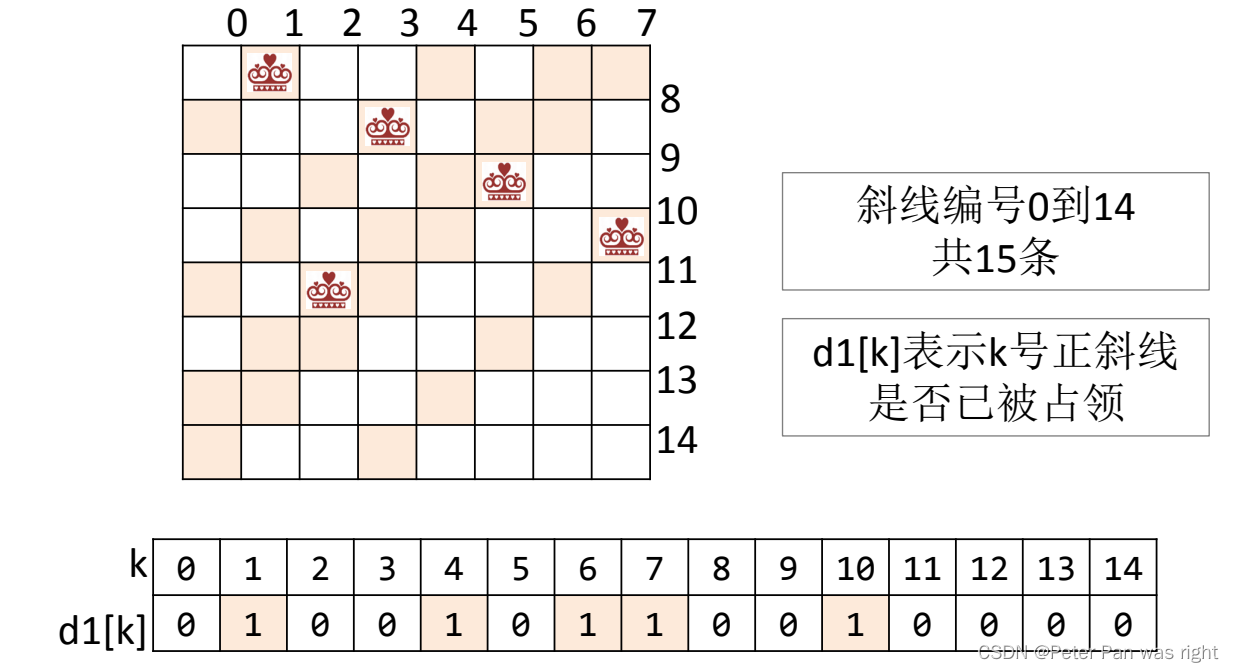
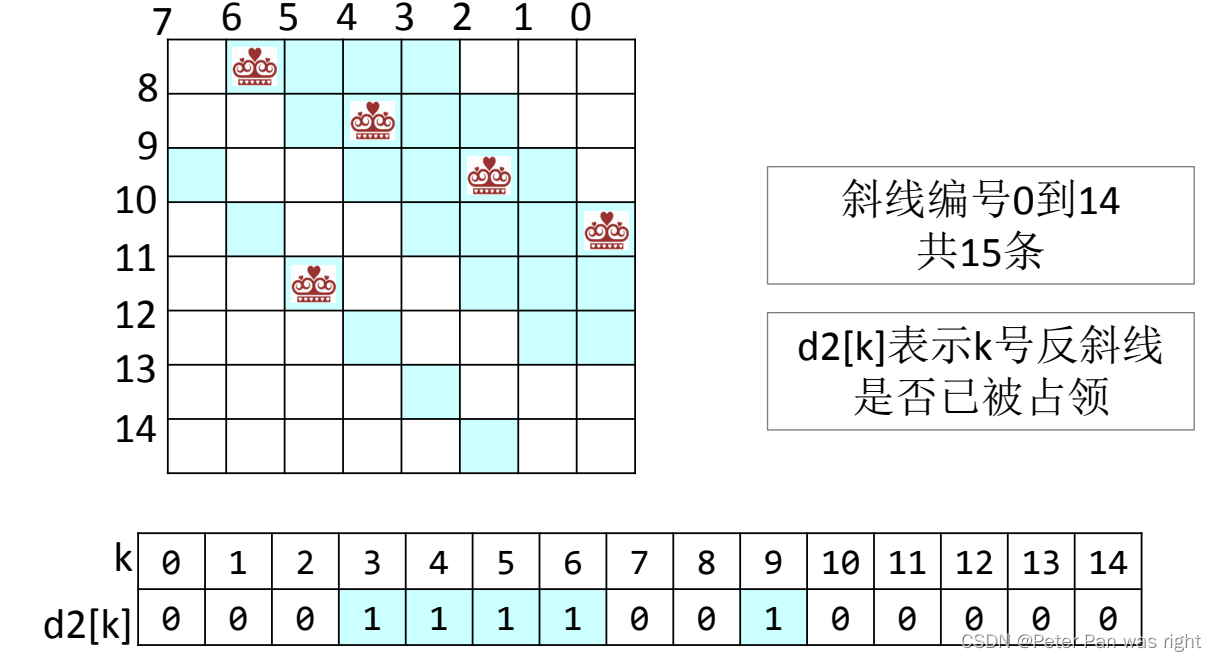  然后再来看dfs函数

void dfs(int x,int y,int c){if(x==N){ans++;print();return;}for(int y=0;y<N;y++)if(valid(x,y)){f[x][y]=clmn[y]=d1[x+y]=d2[x-y+N-1];dfs(x+1);f[x][y]=clmn[y]=d1[x+y]=d2[x-y+N-1];}
}

希望这些对大家有用，三联必回