前言
本文的成就是一个点顺着一个点而来的,成文过程颇有意思
- 首先,如上文所说,我司正在做三大LLM项目,其中一个是论文审稿GPT第二版,在模型选型的时候,关注到了Mistral 7B(其背后的公司Mistral AI号称欧洲的OpenAI,当然 你权且一听,切勿过于当真)
- 而由Mistral 7B顺带关注到了基于其微调的Zephyr 7B,而一了解Zephyr 7B的论文,发现它还挺有意思的,即它和ChatGPT三阶段训练方式的不同在于:
在第二阶段标注排序数据的时候,不是由人工去排序模型给出的多个答案,而是由AI比如GPT4去根据不同答案的好坏去排序
且在第三阶段的时候,用到了一个DPO的算法去迭代策略,而非ChatGPT本身用的PPO算法去迭代策略 - 考虑到ChatGPT三阶段训练方式我已经写得足够完整了(instructGPT论文有的细节我做了重点分析、解读,论文中没有的细节我更做了大量的扩展、深入、举例,具体可以参见《ChatGPT技术原理解析:从RL之PPO算法、RLHF到GPT4、instructGPT》)
而有些朋友反馈到DPO比PPO好用(当然了,我也理解,毕竟PPO那套RL算法涉及到4个模型,一方面是策略的迭代,一方面是价值的迭代,理解透彻确实不容易),所以想研究下DPO - 加之ChatGPT的最强竞品Claude也用到了一个RAILF的机制(和Zephyr 7B的AI奖励/DPO颇有异曲同工之妙),之前也曾想过写来着,但此前一直深究于ChatGPT背后的原理细节,现在也算有时间好好写一写了
综上,便拟定了本文的标题
第一部分 什么是DPO
今年5月份,斯坦福的一些研究者提出了RLHF的替代算法:直接偏好优化(Direct Preference Optimization,简称DPO),其对应论文为《Direct Preference Optimization: Your Language Model is Secretly a Reward Model》
1.1 DPO与RLHF的本质区别
那其与ChatGPT所用的RLHF有何本质区别呢,简言之
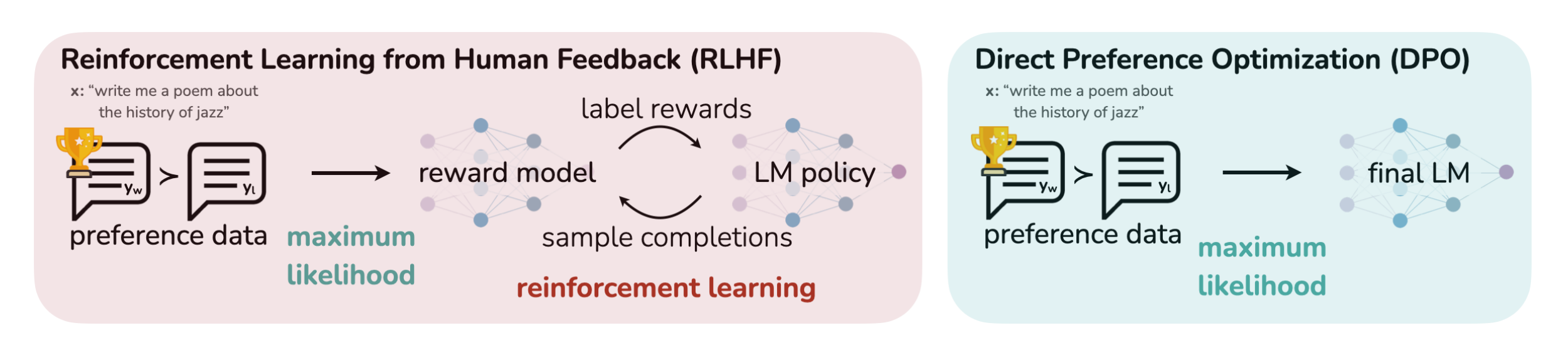
- 在做了SFT之后,RLHF将奖励模型拟合到人类偏好数据集上,然后使用RL方法比如PPO算法优化语言模型的策略
即经典的ChatGPT三阶段训练方式:1) supervised fine-tuning (SFT); 2) preferencesampling and reward learning and 3) reinforcement-learning optimization
虽然RLHF产生的模型具有令人印象深刻的会话和编码能力,但RLHF比监督学习复杂得多,其涉及训练多个LM和在训练循环中从LM策略中采样(4个模型,涉及到经验数据的采集,以及策略的迭代和价值的迭代,如果不太熟或忘了,请参见《ChatGPT技术原理解析》),从而产生大量的计算成本
While RLHF produces models with impressive conversational and coding abilities, the RLHFpipeline is considerably more complex than supervised learning, involving training multiple LMs andsampling from the LM policy in the loop of training, incurring significant computational costs. - 相比之下,DPO通过简单的分类目标直接优化最满足偏好的策略,而没有明确的奖励函数或RL
DPO directly optimizes for the policy best satisfying the preferences with a simple classification objective, without an explicit reward function or RL
更具体而言,DPO的本质在于增加了被首选的response相对不被首选的response的对数概率(increases the relative log probability of preferred to dispreferred responses),但它包含了一个动态的、每个示例的重要性权重,以防止设计的概率比让模型的能力退化(it incorporates a dynamic, per-example importance weight that prevents the model degeneration that we find occurs with a naive probability ratio objective)
与RLHF一样,DPO依赖于理论偏好模型,衡量给定的奖励函数与经验偏好数据的一致性(如果接下来这一段没太看明白,没事 不急,下节1.2节会重点解释,^_^)
- 在SFT阶段,针对同一个prompt
生成答案对
,然后人工标注出
是相对
是更好的答案,接着通过这些偏好数据训练一个奖励模型
那怎么建模偏好损失函数呢,Bradley-Terry(BT)模型是一个常见选择(当然,在可以获得多个排序答案的情况下,Plackett-Luce 是更一般的排序模型)。BT 模型规定人类偏好分布可以表示成
假定我们从上面的分布中采样出来一个数据集
同时,建立我们的奖励模型,然后对其参数做最大似然估计,从而将问题建模为二分类问题,并使用负对数似然损失:
与RLHF类似,其中是logistic函数,
通常从SFT模型
初始化,并在transformer结构的顶部添加一个线性层,该层对奖励值产生单个标量预测
- 接下来,如果是ChatGPT所用的RLHF的话,则是在训练好的奖励模型的指引下迭代策略,其迭代策略的方法是PPO算法
其中,修正项是对奖励函数的修正,避免迭代中的策略
与基线策略
偏离太远
但DPO利用从奖励函数到最优策略的解析映射,这使我们能够将奖励函数上的偏好损失函数转换为策略上的损失函数(our key insight is to leverage an analyticalmapping from reward functions to optimal policies, which enables us to transform a loss functionover reward functions into a loss function over policies)
具体做法是给定人类对模型响应的偏好数据集,DPO使用简单的二元交叉熵目标优化策略,而无需在训练期间明确学习奖励函数或从策略中采样(Given a dataset of human preferences overmodel responses, DPO can therefore optimize a policy using a simple binary cross entropy objective,without explicitly learning a reward function or sampling from the policy during training)
其中
实际上,我们使用 ground-truth 奖励函数的最大似然估计值
,估计配分函数
依然十分困难,这使得这种表示方法在实践中难以利用,那咋办呢?
1.2 DPO的逐步推导:力求清晰易懂
1.2.1 带KL约束奖励的最大化目标的推导(特别是公式3到4)
我们从头到尾梳理一下,且以下第几点则代表公式几
- 公式3:
- 通过上面公式3,可以得到公式4:
————————————————
这一步很关键,是怎么推导出来的呢?
对于公式3,一方面有
还是针对公式3,另一方面,假定在奖励函数下的最优策略为
,公式3的目标自然便是要得到最优策略,因此公式3等价于最小化
与
的KL散度,即有
因此,结合上面针对公式3两个方面的推导,可得
从而有与
正相关,因此不妨设
其中
这个函数只与
和基线策略
有关,而不依赖于策略
,其目的是使得右边满足取值在
,相当于起到一个归一化的效果
- 为了根据其对应的最优策略
、基线策略
和未知的配分函数
,来表示奖励函数
首先对上面公式4
的两边取对数,然后通过一些代数运算得到公式5
假定最优奖励函数下对应的最优模型策略是
,则有
- 考虑到最优策略不确定,因此先用参数化的策略
来表示,相应的奖励函数即可表示为
- 接下来,便可以为策略
构建最大似然目标
类似于奖励建模方法(甚至你可以简单粗暴的认为,即是把上面公式6直接代入进公式2中:)
即最大化偏好答案与非偏好答案奖励的差值,我们的策略目标变为:
完美! 你会发现,如阿荀所说,推导出奖励函数和策略
的联系,就是为了把公式2所示的ranking loss中的
换掉,从而也就完美实现了DPO的目标:根本就不需要训练奖励函数(这一句话便道出了DPO的本质目标,但很多文章不会如此一针见血的指出来)
进一步,上面公式7所表达的目标函数表示的到底啥意思?意思就是
- 当一个答案是好的答案时,我们要尽可能增大其被策略模型生成的概率(且这个的概率尽可能大于被基线模型生成的概率,举个例子,既然是好的,就要比初期更大胆的趋近之)
- 当一个答案是差的答案时,我们要尽可能降低其被策略模型生成的概率(且这个的概率尽可能小于被基线模型生成的概率,换言之,既然是差的,则要比初期尽可能远离之)
还不够直白?OK,我们换个表达方式
由于我们追求的是让目标函数最大(虽说我们一般要求loss最小化,但毕竟整个目标函数的最前面加了个负号),故意味着针对大括号里的这个式子而言
我们希望左边尽可能大,而右边尽可能小,那左边、右边分别意味着什么呢?
- 左半部分代表good response相较于没训练之前的累积概率差值
- 右半部分代表 bad response 相较于没训练之前的累计概率差值
有三种可能的情况
- 左边变大,右边变小,理想情况,good response概率提升,bad response概率下降
- 左边变小,右边更小,good response概率下降,但是bad response概率下降的更多,生成的时候还是倾向于good response
- 左边变的更大,右边只大了一点点,和2) 同理
相当于奖与惩必须越发拉开差距
- 如果是好的,就该被尽可能奖励(即good response对应的奖励应尽可能大),且得到的
比初期更多
- 如果是差的,则要被尽可能惩罚(即 bad response 对应的奖励应尽可能小),且得到的
比初期更小
1.2.2 求解DPO目标函数梯度的推导
为了进一步理解DPO,求解下上述公式7的梯度
- 令
则有
根据sigmoid函数的性质以及
,可得
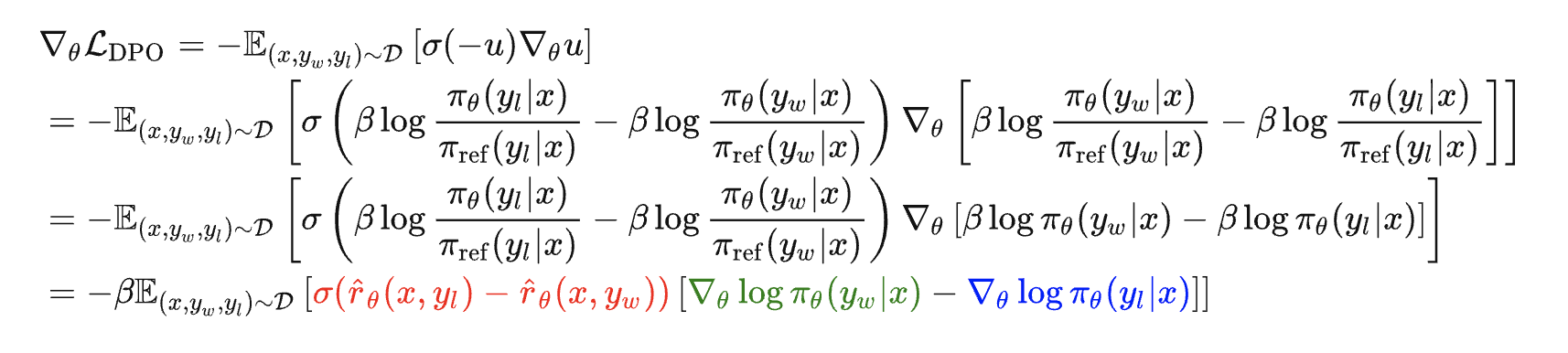
其中
由优化策略和基线策略
定义(在 DPO的论文中,该修正项称为隐式奖励模型)
至于红色部分表示当非偏好答案的奖励大于偏好答案
的奖励时,梯度越大,而损失函数的梯度会增加生成偏好回答
的概率(对应绿色部分),降低非偏好回答
的概率(对应蓝色部分)
// 待更
第二部分 Zephyr 7B:基于Mistral 7B微调且采取AIF + DPO
2.1 7B小模型的基准测试超过70B
机器学习社区hugging face发布了一款名为Zephyr 7B的基座模型,其基于Mistral 7B微调而成,与ChatGPT用的RLHF不太一样的是,它用的是AIF + DPO,最终在一系列基准测试中超越了LLAMA2-CHAT-70B(当然了,基准测试超越不一定就说明代表全方位的超越,要不然国内的都超越GPT4了)

2.2 三步骤训练方式:SFT AIF DPO
如下图所示,便是Zephyr的三步骤训练方式(注意,和ChatGPT的三阶段训练方式有着本质不同,Zephyr的三步骤训练方式中的步骤二只是AI标注数据,不涉及奖励模型的训练)
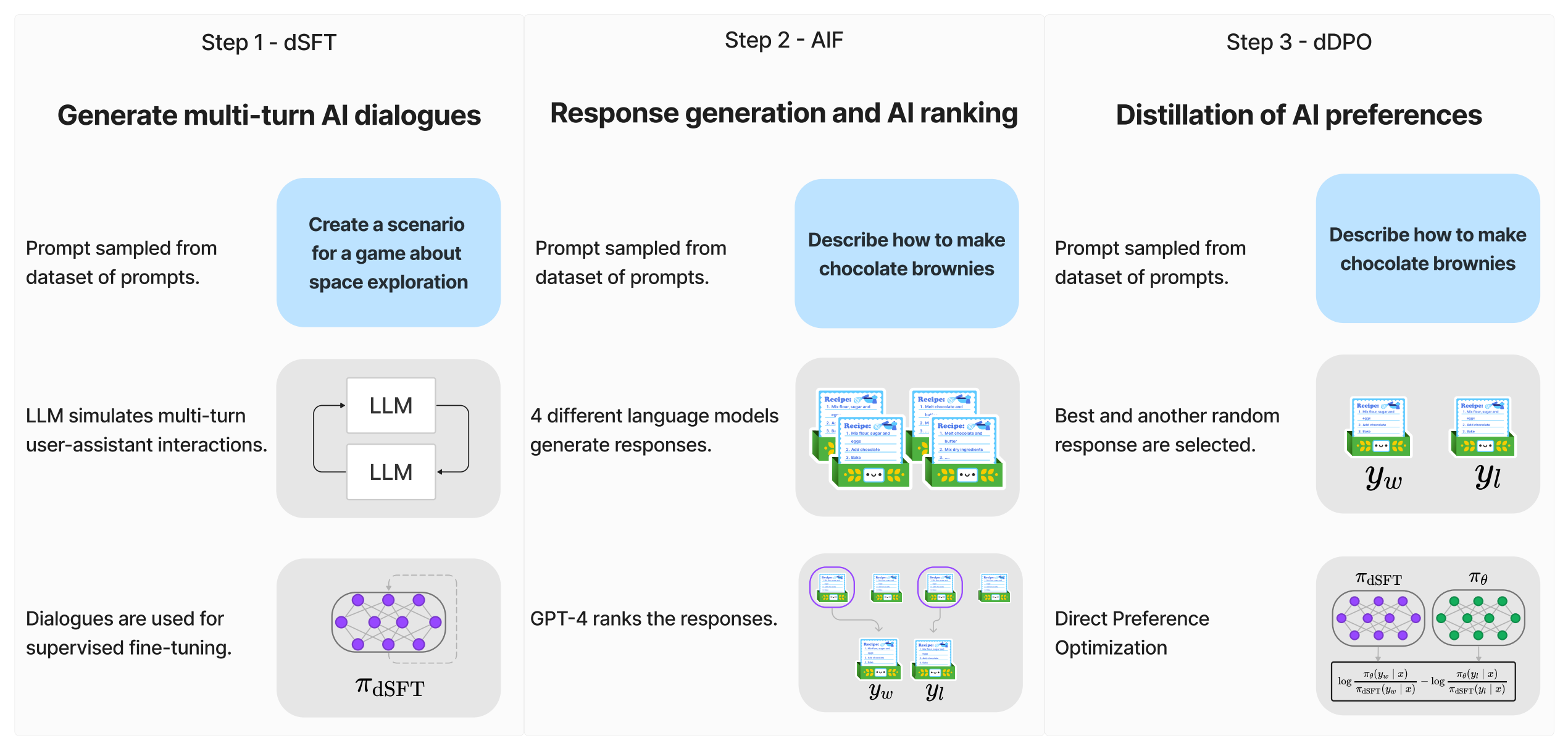
- 通过大规模、自指导式数据集(UltraChat)做精炼的监督微调(dSFT)
large scale, self-instruct-style dataset construction(UltraChat), followed by distilled supervised fine-tuning (dSFT)
注意,UltraChat是一个 self-refinement的数据集,由GPT-3.5-TURBO生成的超过30个主题和20种不同类型的文本材料组成的1.47M多轮对话数据 - 通过集成收集AI反馈(AIF)聊天模型完成情况,然后通过GPT-4(UltraFeedback)进行评分并二值化为偏好
AI Feedback (AIF) collection via an ensemble of chat model completions, followed by scoring by GPT-4 (UltraFeedback) and
binarization into preferences
注意,UltraFeedback由64k的prompts组成,每个prompt都有四个LLM生成的response,GPT-4根据遵循指令、诚实和乐于助人等标准对这些响应进行评级
且通过选择最高平均分数作为“选择”响应,并随机选择其余三个中的一个作为“拒绝”响应,从UltraFeedback构建二元偏好(We construct binary preferences from UltraFeedback by selecting the highest mean score as the “chosen” response and one of the remaining three at random as “rejected”)
我们选择随机选择,而不是选择得分最低的响应,以鼓励多样性并使DPO目标更具挑战性(We opted for random selection instead of selecting the lowest-scored response to encourage diversity and make the DPO objective more challenging)
如上所述,此步骤是离线计算的,不涉及基线模型的任何采样 - 利用反馈数据对dSFT模型进行直接偏好优化(dPO)
distilled direct preference optimization (dPO) of the dSFT model utilizing the feedback data
2.2.1 三步骤训练方式的细节
假定是一系列prompts数据,被构造为代表一组不同的主题域
- Distilled Supervised Fine-Tuning (dSFT)
对于每个, 先对response
进行采样,然后通过采样新指令进行细化:
,最终数据集为:
,通过SFT进行蒸馏
- AI Feedback through Preferences (AIF)
与SFT一样,针对中的每一个prompt x,收集4个不同模型的response(比如Claude、Falcon、LLaMA等,这点与ChatGPT也不太一样,ChatGPT是针对同一个prompt采集同一个模型不同概率下的4个输出):
注意,接下来,便是与ChatGPT不同的地方了(ChatGPT是人工排序),Zephyr会把这些responses给到GPT-4,让GPT4给这些response打分并排序:收集到各个prompt的分数后,将得分最高的response保存为,并随机将一个较低的得分保存为
,最终的反馈数据集是一个个三元组
上述步骤在论文中的描述如下图所示

- Distilled Direct Preference Optimization (dDPO) 第三步是通过最大化偏好模型中首选
而非
的概率来进一步微调SFT模型( The goal of the final step is to refine the πdSFT by maximizing the likelihood of ranking the preferred yw over yl in a preference model )
而这个偏好模型通过利用需要迭代的策略模型的奖励函数
来确定( is determined by a reward function rθ(x, y) which utilizes the student language model πθ )
不同于ChatGPT通过PPO算法去迭代策略(涉及到通过旧策略采集经验数据),直接偏好算法DPO使用更简单的方法,即直接依据静态数据去优化偏好模型( Direct preference optimization (DPO) uses a simpler approach to directly optimize the preference model from the static data )
其中的关键便是根据模型的最优策略与SFT策略推导出最优的奖励函数( The key observation is to derive the optimal reward function in terms of the optimal LLM policy π∗ and the original LLM policy π dSFT )
在合适的偏好模型的情况下,对于常数和配分函数
有
接着将奖励函数插入到偏好模型中,便可以得到目标函数( 发现没有,直接把奖励函数给消掉消没了 )
基于这个目标函数,我们从模型的SFT版本开始,迭代每个AIF下的三元组
1) 根据SFT模型计算和
的概率
2) 根据DPO模型计算和
的概率
3) 优化上述目标函数,然后做反向传播以更新
第三部分 Claude的RAILF
// 待更
参考文献与推荐阅读
- ChatGPT技术原理解析:从RL之PPO算法、RLHF到GPT4、instructGPT
- DPO原始论文:Direct Preference Optimization: Your Language Model is Secretly a Reward Model
- DPO——RLHF 的替代之《Direct Preference Optimization: Your Language Model is Secretly a Reward Model》论文阅读
DPO: Direct Preference Optimization 论文解读及代码实践 - DPO: Direct Preference Optimization训练目标推导,推导简练易懂,推荐
- Zephyr 7B原始论文:ZEPHYR: DIRECT DISTILLATION OF LM ALIGNMENT
创作、修改、完善记录
- 11.6日,写第一部分 什么是DPO
且反复对比介绍DPO的各篇文章,研究如何阐述才是最清晰易懂的 - 11.7日,在一字一句抠完Zephyr 7B的论文之后,开始写本文的“第二部分 Zephyr 7B三步骤训练方式:SFT AIF DPO”
- 11.8日,优化1.2节中关于DPO目标函数的描述,使其描述尽可能清晰、明确、易懂
且部分细节与七月黄老师(阿荀)讨论确认,补充了一些表达上更本质的描述(比如加了很关键的一句话:“推导出奖励函数和策略
的联系,就是为了把公式2所示的ranking loss中的
换掉,从而也就完美实现了DPO的目标:根本就不需要训练奖励函数”)
以及修正了一些不够严谨/精准的描述(比如对于Zephyr 7B而言,表达为三步骤训练方式,比表达为三阶段训练方式更正确) - //..
)




)

)



-CRC校验介绍算法)


)




