目录
一、贝叶斯方法
背景知识
贝叶斯公式
二、朴素贝叶斯原理
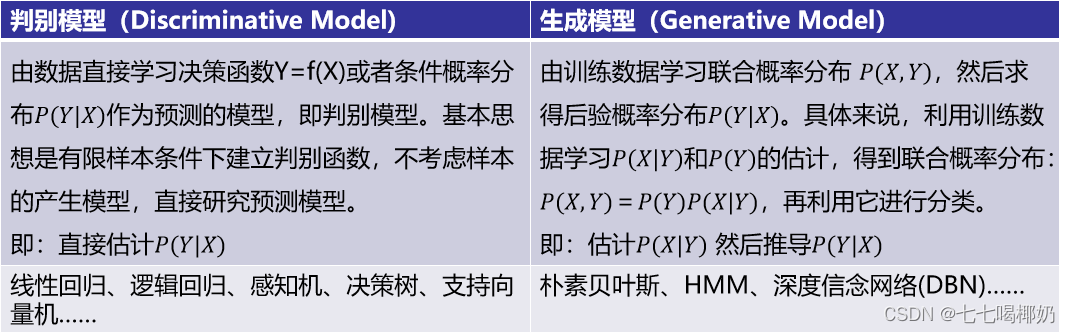
判别模型和生成模型
1.朴素贝叶斯法是典型的生成学习方法
2.朴素贝叶斯法的基本假设是条件独立性
3.朴素贝叶斯法利用贝叶斯定理与学到的联合概率模型进行分类预测
用于文本分类的朴素贝叶斯模型:
三、朴素贝叶斯案例
四、朴素贝叶斯代码实现
一、贝叶斯方法
背景知识
- 贝叶斯分类:贝叶斯分类是一类分类算法的总称,这类算法均以贝叶斯定理为基础,故统称为贝叶斯分类。
- 先验概率:根据以往经验和分析得到的概率。我们用P(Y)来代表在没有训练数据前假设Y拥有的初始概率。
- 后验概率:根据已经发生的事件来分析得到的概率。以P(Y|X)代表假设X 成立的情下观察到Y数据的概率,因为它反映了在看到训练数据X后Y成立的置信度。
- 联合概率:联合概率是指在多元的概率分布中多个随机变量分别满足各自条件的概率。X与Y的联合概率表示为P(X,Y)、 P(XY) 或P(X∩Y) 。假设X和Y都服从正态分布,那么P(X<5,Y<0)就是一个联合概率,表示 X<5,Y<0两个条件同时成立的概率。表示两个事件共同发生的概率。
贝叶斯公式

朴素贝叶斯法是典型的生成学习方法。生成方法由训练数据学习联合概率分布 P(X,Y),然后求得后验概率分布P(Y|X)。
学习联合概率的方法:利用训练数据学习P(X|Y)的估计,与先验的P(Y)相乘,得到 P(X,Y)=P(X|Y) P(Y)
二、朴素贝叶斯原理
判别模型和生成模型
监督学习方法又分 生成方法(Generative approach)和判别方法(Discriminative approach)
所学到的模型分别称为 生成模型(Generative Model)和判别模型(Discriminative Model)。
1.朴素贝叶斯法是典型的生成学习方法
生成方法由训练数据学习联合概率分布 P(X,Y),然后求得后验概率分布P(Y|X)。具体来说,利用训练数据学习P(X|Y)和P(Y)的估计,得到联合概率分布:
概率估计方法可以是极大似然估计或贝叶斯估计。
2.朴素贝叶斯法的基本假设是条件独立性
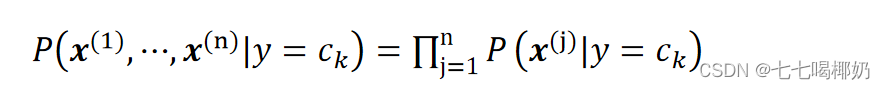
c_k代表类别,k代表类别序号。
这是一个较强的假设。由于这一假设,朴素贝叶斯法的学习与预测大为简化。因而朴素贝叶斯法高效,且易于实现。其缺点是分类的性能不一定很高。
3.朴素贝叶斯法利用贝叶斯定理与学到的联合概率模型进行分类预测
我们要求的是P(Y|X),根据生成模型定义我们可以求P(X,Y)和P(Y)。 这个称作朴素贝叶斯假设条件独立,形式化表示为: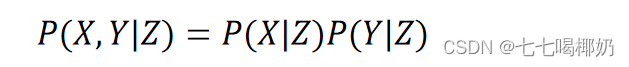 (给定Z的情况下,X、Y条件独立)
(给定Z的情况下,X、Y条件独立)
也可以表示为: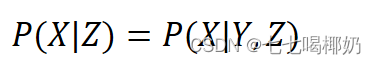
用于文本分类的朴素贝叶斯模型:
首先随机选定了邮件的类型y(垃圾邮件或普通邮件),然后一个人翻遍词典的所有词,依照概率p(x^(i)|y)随机决定一个词是否出现,出现标示为1,否则标示为0 。假设有50000个单词,那么这封邮件的概率可以表示为: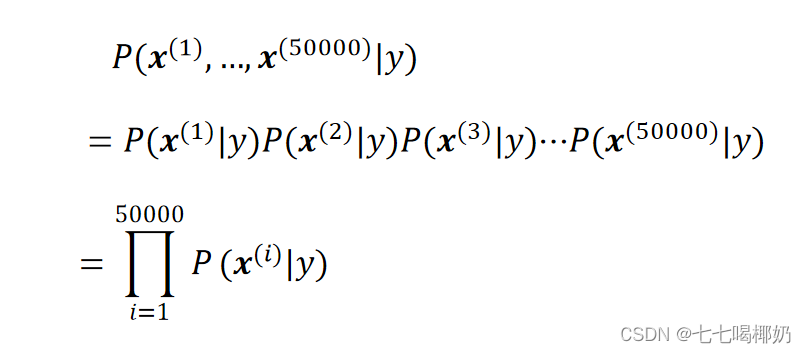
联合概率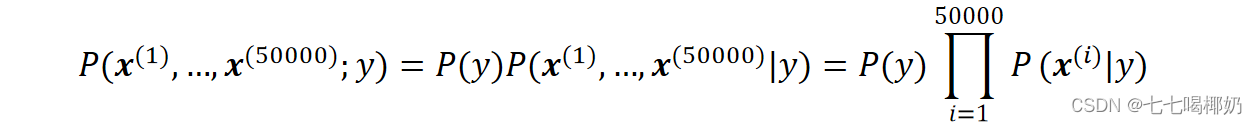 将输入x分到联合概率最大的类 y ̂ :
将输入x分到联合概率最大的类 y ̂ :
三、朴素贝叶斯案例
假设我们正在构建一个分类器,该分类器说明文本是否与运动(Sports)有关。我们的训练数据有5句话: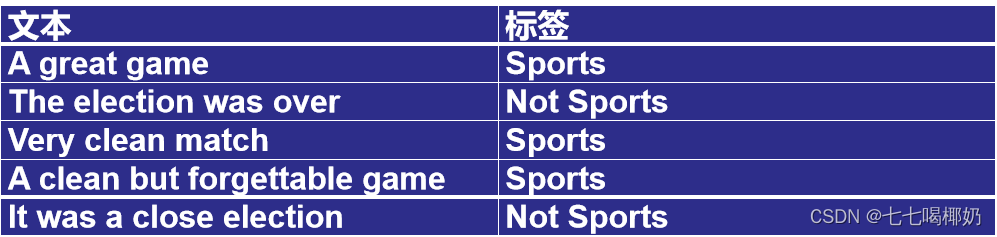
我们想要计算句子“A very close game”是 Sports 的概率以及它不是 Sports 的概率。
P( Sports | a very close game ) 即这个句子的类别是Sports的概率
特征:单词的频率
已知贝叶斯定理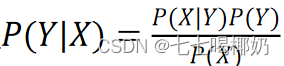 ,则:
,则:
由于我们只是试图找出哪个类别有更大的概率,可以舍弃除数,只是比较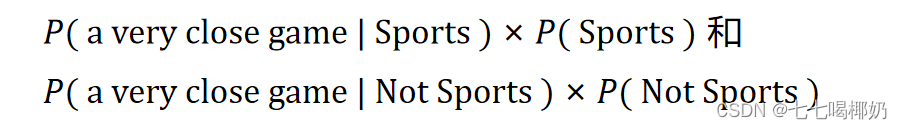 我们假设一个句子中的每个单词都与其他单词无关。
我们假设一个句子中的每个单词都与其他单词无关。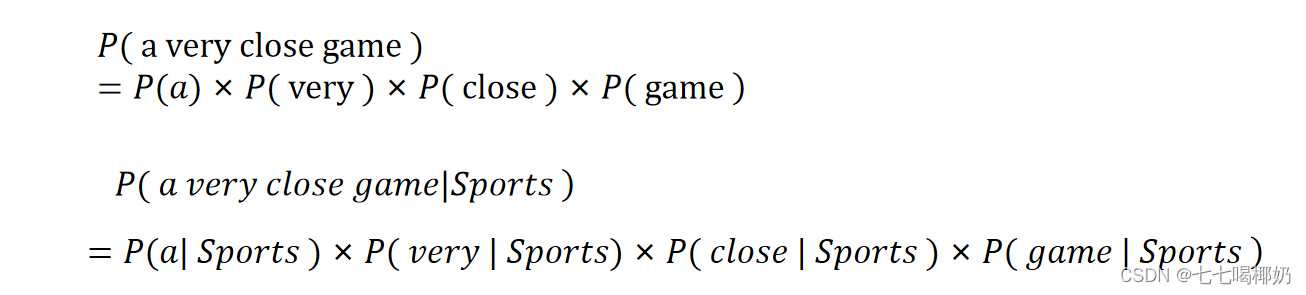
计算每个类别的先验概率:
对于训练集中的给定句子,P(Sports )的概率为⅗。P(Not Sports )是⅖。
然后,再计算P(game│Sports)就是“game”有多少次出现在Sports的样本,然后除以sports为标签的文本的单词总数(3+3+5=11)。
因此,P(game│Sports)=2/11。
“close”不会出现在任何sports样本中!那就是说P(close│Sports)=0。
通过使用一种称为拉普拉斯平滑的方法:我们为每个计数加1,因此它永远不会为零。为了平衡这一点,我们将可能单词的数量添加到除数中,因此计算结果永远不会大于1(且保证了最终和为1的概率性质)。
在这里的情况下,可能单词是['a', 'great', 'very', 'over', 'it', 'but', 'game', 'election', 'clean', 'close', 'the', 'was', 'forgettable', 'match']。
由于可能的单词数是14,因此应用平滑处理可以得到 P( game | sports )=(2+1)/(11+14)
拉普拉斯平滑是一种用于平滑分类数据的技术。引入拉普拉斯平滑法来解决零概率问题,通过应用此方法,先验概率和条件概率可以写为
其中K表示类别数量,A表示a_j中不同值的数量,通常λ=1 加入拉普拉斯平滑之后,避免了出现概率为0的情况,又保证了每个值都在0到1的范围内,又保证了最终和为1的概率性质。


四、朴素贝叶斯代码实现
最常用的GaussianNB是高斯贝叶斯分类器。它假设特征的条件概率分布满足高斯分布:


其他贝叶斯分类器:
- MultinomialNB是多项式贝叶斯分类器,它假设特征的条件概率分布满足多项式分布;
- BernoulliNB是伯努利贝叶斯分类器。它假设特征的条件概率分布满足二项分布。
GaussianNB是高斯朴素贝叶斯分类器的scikit-learn实现。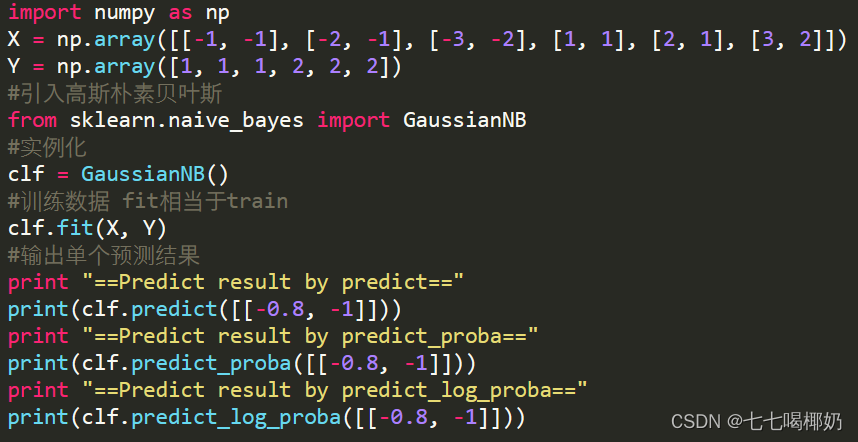
GaussianNB是高斯朴素贝叶斯分类器的Numpy实现。 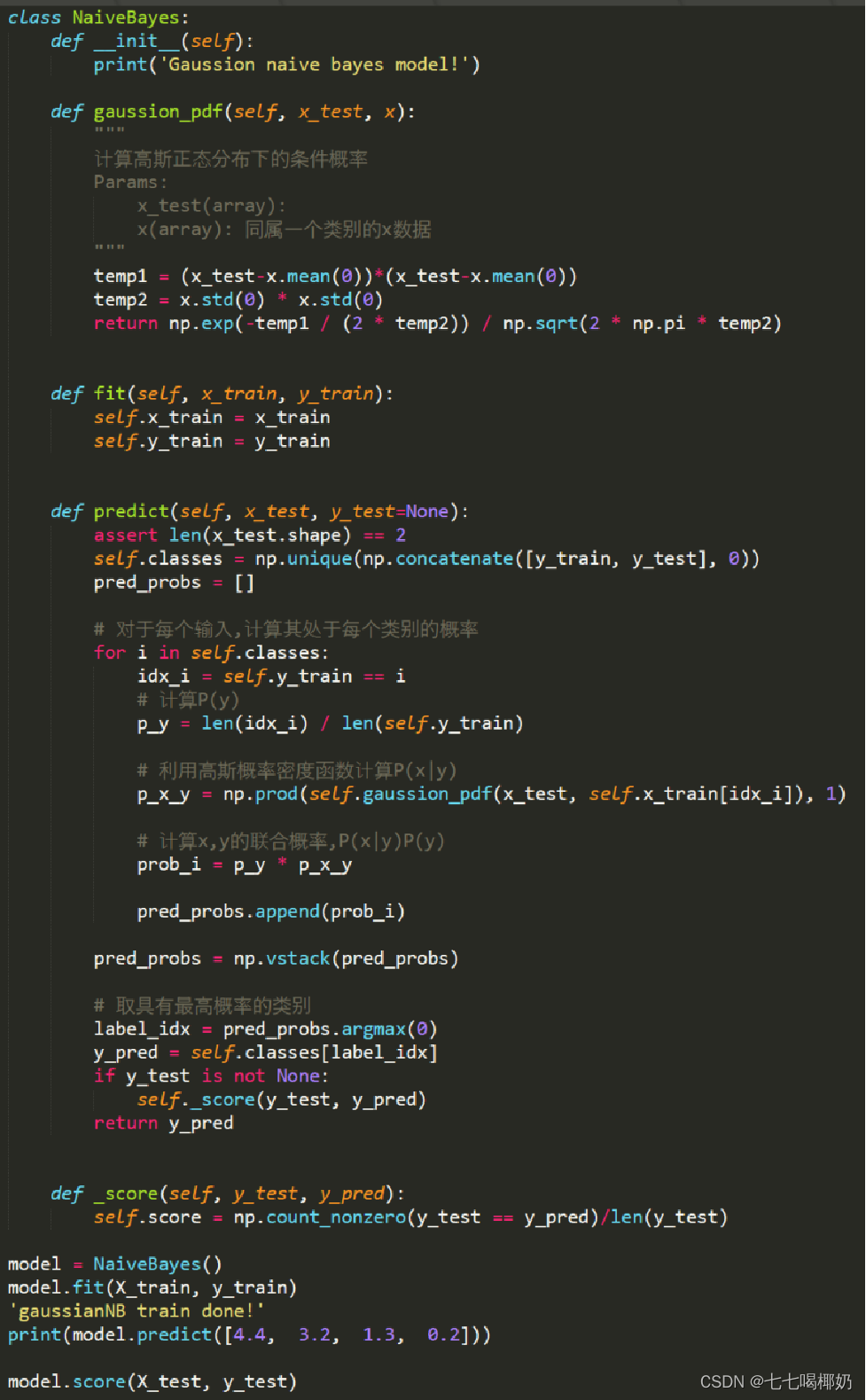
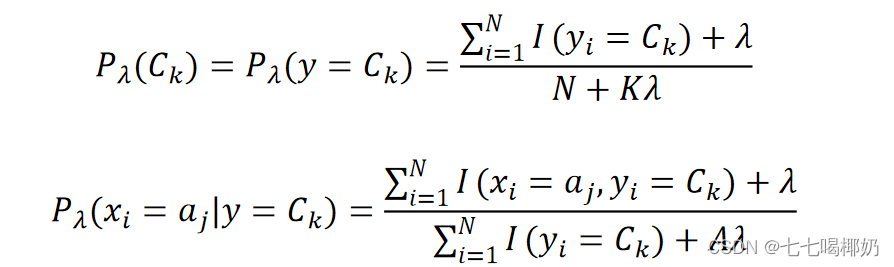







)
![即时通讯技术文集(第22期):IM安全相关文章(Part1) [共13篇]](http://pic.xiahunao.cn/即时通讯技术文集(第22期):IM安全相关文章(Part1) [共13篇])
![用友NC Cloud accept.jsp接口任意文件上传漏洞复现 [附POC]](http://pic.xiahunao.cn/用友NC Cloud accept.jsp接口任意文件上传漏洞复现 [附POC])


![[yarn]yarn异常](http://pic.xiahunao.cn/[yarn]yarn异常)

:用于计算非支配(non-dominated)前沿)

--模板与范型编程)


