AVL树详解

AVL树的概念

旋转的介绍

单旋转

双旋转

旋转演示

具体实现

通过高度判断的实现

通过平衡因子判断的实现

AVL树的概念

AVL树是一种自平衡的平衡二叉查找树，它是一种高效的数据结构，可以在插入和删除节点时保持树的平衡，从而保证树的操作时间复杂度能够达到O(log n)。

所谓平衡就是保证每个节点的左右子树的高度差不能超过1。例如

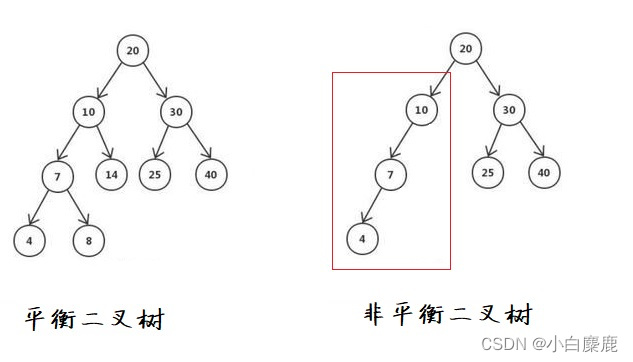
对AVL树进行插入或删除操作时，可能会导致某些节点的高度差超过1，即不再平衡。这时就需要进行旋转操作来恢复AVL树的平衡性。所以，AVL树的核心内容就是旋转。

旋转的介绍

一般来讲，我们将旋转类型分为两大类。左-左、右-右类型的为单旋转，左-右、右-左类型的为双旋转。下面是这四种旋转的操作方式。

单旋转

AVL树的单旋转指的是在树的某个节点上进行的一种旋转操作，通过左旋或右旋使该节点成为旋转后的子树的根节点，并使树保持平衡状态。在单旋转过程中，节点的左右子树高度变化不超过1，旋转操作其实是把子树的位置进行调整，使得整棵树的平衡因子尽可能地符合平衡树的要求。

具体来说，如果在某个节点的左子树中插入了一个新节点导致该节点的左子树高度比右子树高度多2，那么就需要在该节点进行一次右旋转操作。右旋转将该节点的左子节点变为子树的根节点，该节点的原父节点成为子树的新根节点的右子节点，子树的其他节点位置不变。

同理，如果在某个节点的右子树中插入了一个新节点导致该节点的右子树高度比左子树高度多2，那么就需要在该节点进行一次左旋转操作。左旋转将该节点的右子节点变为子树的根节点，该节点的原父节点成为子树的新根节点的左子节点，子树的其他节点位置不变。

具体的图解如下：

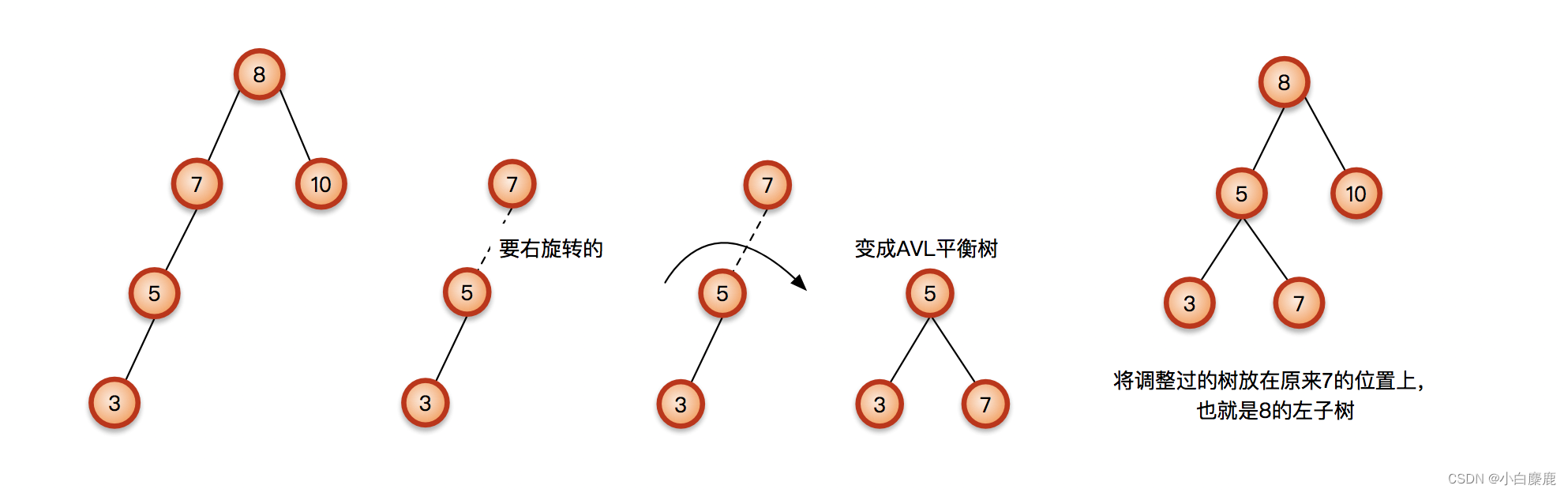
图片出处：AVL树的旋转图解和简单实现_avl树旋转-CSDN博客

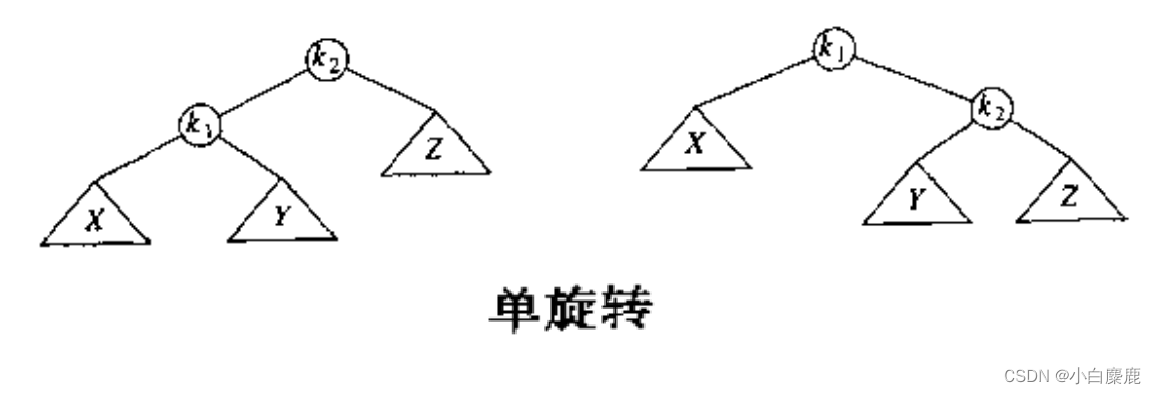
单旋转的过程可以概况为如下的三个步骤（以下图为模型，以单左旋为例）：

1、让k2原本指向k1的指针现在指向k1内侧的节点

2、让k1原本指向内侧的指针现在指向k2

3、让原来指向k2的指针现在改为指向k1，并更新各节点的高度

双旋转

AVL树的双旋转是指在某个节点的子树中进行两次旋转操作以保持平衡的一种树旋转方式。双旋转包含两种情况：左旋-右旋和右旋-左旋。

具体来说，假设在AVL树的某个节点的左子树中插入了一个新节点，导致该节点的左子树高度比右子树高度多2，但是进行一次右旋转不能转换成平衡状态，此时需要进行左旋-右旋操作。该操作可以分解为两步：

对该节点的左子节点进行一次左旋转。

对该节点进行一次右旋转。

左旋转操作会使得该节点的左子节点变为子树的根节点，同时该节点成为新根节点的右子节点，然后对该节点进行右旋转时，子树的根节点发生了变化，新的根节点是之前的左子节点，原本的根节点成为新节点的右子节点，最后使得整棵树重新平衡。

同样的，假如在AVL树的某个节点的右子树中插入了一个新节点，导致该结点的右子树高度比左子树高度多2，但进行一次左旋转不能转换成平衡状态，此时需要进行右旋-左旋操作。该操作可以分成两步：

对该节点的右子节点进行一次右旋转。

对该节点进行一次左旋转。

右旋转操作会使得该节点的右子节点变为子树的根节点，同时该节点成为新根节点的左子节点，然后对该节点进行左旋转时，子树的根节点发生了变化，新的根节点是之前的右子节点，原本的根节点成为新节点的左子节点，最后使得整棵树重新平衡。

具体图解如下：

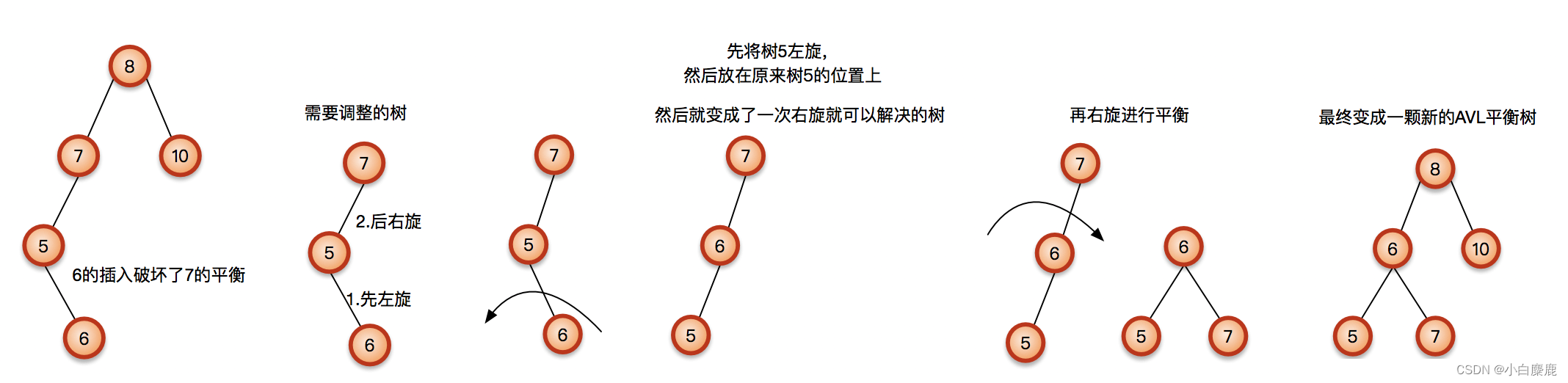
图片出处：AVL树的旋转图解和简单实现_avl树旋转-CSDN博客

双旋转其实就是两次单旋转，先将内侧的节点通过单旋转“移出来”到外侧。然后再用一次单旋转，最终成为我们想要的平衡状态。

旋转演示

AVL树动画演示

也可以自己尝试：

AVL Tree Visualzation (usfca.edu)https://www.cs.usfca.edu/~galles/visualization/AVLtree.html

具体实现

通过高度判断的实现

AVL树一个最直接的方式就是每个节点的信息中增加了一个高度信息(Height)，每个节点在插入后向上回溯到根，进行高度信息的调整更新，并判断是否要进行旋转。这种实现方式比较直观好想，每次判断是否需要进行旋转的时候就直接判断高度差即可。

如下是一种实现方式（C语言实现，以递归的方式进行插入和回溯，每个节点只有左右孩子两个指针，维护平衡条件的信息是节点的高度），仅供参考。

/* 忽略了相关头文件 */typedef char ElementType; //暂定节点内容只有单个字符typedef struct AvlTreeNode
{ElementType Data; int Height;struct AvlTreeNode* Left;struct AvlTreeNode* Right;
}AvlTree; int Height(AvlTree* Node)
{if (Node == NULL)return -1;return Node->Height;
}
AvlTree* SingleLeftRotate(AvlTree* k2) //单左旋，LL旋转（k2的由来详见数据结构与算法分析P94）
{//旋转节点AvlTree* k1 = k2->Left; k2->Left = k1->Right;k1->Right = k2;//更新高度k2->Height = max(Height(k2->Left), Height(k2->Right)) + 1;k1->Height = max(Height(k1->Left), Height(k1->Right)) + 1;//返回return k1;
}
AvlTree* SingleRightRotate(AvlTree* k2) //单右旋，RR旋转（k2的由来详见数据结构与算法分析P94）
{//旋转节点AvlTree* k1 = k2->Right;k2->Right = k1->Left;k1->Left = k2; //更新高度k2->Height = max(Height(k2->Left), Height(k2->Right)) + 1;k1->Height = max(Height(k1->Left), Height(k1->Right)) + 1;//返回return k1;
}
AvlTree* DoubleLRRotate(AvlTree* k3) //双左右旋，LR旋转（k3的由来详见数据结构与算法分析P95）
{/*一次双旋转等于两次单旋转。可以理解为先将需要旋转的移至同一方向（即左左、右右这种），然后再用单旋转的方式处理*/k3->Left = SingleRightRotate(k3->Left); return SingleLeftRotate(k3);  
}
AvlTree* DoubleRLRotate(AvlTree* k3) //双右左旋，RL旋转（k3的由来详见数据结构与算法分析P95）
{/*一次双旋转等于两次单旋转。可以理解为先将需要旋转的移至同一方向（即左左、右右这种），然后再用单旋转的方式处理*/k3->Right = SingleLeftRotate(k3->Left);return SingleRightRotate(k3);
}
AvlTree* InsertElement(AvlTree** root, ElementType data)
{//走到空节点（即插入位置），执行插入操作if ((*root) == NULL){//开辟空间并赋值*root = (AvlTree*)calloc(1, sizeof(AvlTree));//成功开辟空间if ((*root) != NULL)(*root)->Data = data; //开辟空间失败else	puts("heap area is full!");} //根节点无内容（值为0），说明为空树，则直接将data插入到根节点else if ((*root)->Data == 0) {(*root)->Data = data;}//data比节点内容小，在左侧插入else if (data < (*root)->Data) {//向左走，并更新左子树内容(*root)->Left = InsertElement(&(*root)->Left, data);	//判断是否需要旋转if (Height((*root)->Left) - Height((*root)->Right) == 2){//如果data小于左子树的data，说明是data插入到左子树的左节点，符合单旋转的情况（3个节点都在左侧）if (data < (*root)->Left->Data) *root = SingleLeftRotate(*root); //左侧单旋转，并更新节点内容//如果data不小于左子树的data，说明是插入到左子树的右节点，是LR型的双旋转情况else*root = DoubleLRRotate(*root); //左右双旋转，并更新节点内容}}//data比节点内容大，在右侧插入else if (data > (*root)->Data) {//向右走，并更新左子树内容(*root)->Right = InsertElement(&(*root)->Right, data); //判断是否旋转if (Height((*root)->Right) - Height((*root)->Left) == 2) {//如果data大于右子树的data，说明是data插入到右子树的右节点，符合单旋转的情况（3个节点都在右侧）if (data > (*root)->Right->Data) *root = SingleRightRotate(*root);  //右侧单旋转，并更新节点内容//如果data不大于右子树的data，说明是插入到右子树的左节点，是RL型的双旋转情况else*root = DoubleRLRotate(*root);}}//data与节点内容值相同else {  /*暂定如果插入的元素内容相同，则什么都不做*/  }//最后更新节点高度(*root)->Height = max(Height((*root)->Left), Height((*root)->Right)) + 1; //返回return *root;
}

通过平衡因子判断的实现

相比通过高度的直观，平衡因子就有些复杂了。这里的平衡因子指的是右子树的高度减左子树的高度，每个节点都有一个平衡因子信息，初始化为0。每次插入节点后也是向上回溯，进行平衡因子的更新调整与判断是否需要旋转，不过这种方式不一定要走到根，如果更新后的平衡因子信息为0，就说明不用再往上调了。

如下是一种实现方式（C++实现，通过迭代循环的方式进行插入和回溯，为了能够不通过递归进行回溯操作，除了基准的左右儿子指针，这种实现方式为每一个节点还为维护了一个双亲指针，维护平衡条件的信息是平衡因子），仅供参考。

/* 忽略了相关头文件 */// 节点类型
template<typename T>
struct AVLNode
{AVLNode(const T& val): _val(val), _left(nullptr), _right(nullptr), _parent(nullptr), _bf(0){}T _val;  // 数据内容int _bf; // 平衡因子：右高度减左高度AVLNode<T>* _left;AVLNode<T>* _right;AVLNode<T>* _parent;
};// 树的类型
template<typename T>
class AVLtree
{AVLNode<T>* _root = nullptr; // 根节点
public:bool insert(const T& val){/* 初始情况，树为空 */if (_root == nullptr){_root = new AVLNode<T>(val);return true;}/* 一般情况，插入数据 */AVLNode<T>* pre = nullptr;AVLNode<T>* cur = _root;// 先找到对应位置while (cur){// 要插入数据已存在 - 插入失败if (val == cur->_val)return false;// 要插入数据不存在，继续寻找pre = cur;if (val > cur->_val)cur = cur->_right;else if (val < cur->_val)cur = cur->_left;}// cur找到了插入位置，new一个新节点并插入cur = new AVLNode<T>(val);if (val > pre->_val)pre->_right = cur;elsepre->_left = cur;cur->_parent = pre;/* 向上回溯，随之更新平衡因子，并进行旋转调整 */while (pre != nullptr){// 根据cur的位置，更新父节点的平衡因子信息if (cur == pre->_right)pre->_bf++;elsepre->_bf--;// bf为0或者正负2的情况都退出，所以就合并处理了// 因为2这里给限制死了，所以不会出现abs(bf)大于等于3的情况if (abs(pre->_bf) != 1){if (abs(pre->_bf) == 2)rotatenode(pre, cur->_bf);break;}// 没遇到特殊情况，继续向上回溯cur = pre;pre = cur->_parent;}return true;}
private:// 需要旋转节点的情况 - 旋转的4种情况void rotatenode(AVLNode<T>* parent, int cur_bf){if (parent->_bf == 2){if (cur_bf == 1)rotateRR(parent);else if (cur_bf == -1)rotateRL(parent);}else if (parent->_bf == -2){if (cur_bf == 1)rotateLR(parent);else if (cur_bf == -1)rotateLL(parent);}}/* 旋转的4个函数 */// 左左单旋（节点都在左侧的情况）void rotateLL(AVLNode<T>* parent){		// 调整节点位置及父子关系AVLNode<T>* cur = parent->_left;AVLNode<T>* rchild = cur->_right;parent->_left = rchild;if (rchild != nullptr)rchild->_parent = parent;cur->_right = parent;// 进行旋转AVLNode<T>* super = parent->_parent;cur->_parent = super;parent->_parent = cur;AVLNode<T>*& port = super == nullptr ? _root : (super->_left == parent ? super->_left : super->_right);port = cur;// 调节平衡因子cur->_bf = 0;parent->_bf = 0;}// 右右单旋（节点都在右侧的情况）void rotateRR(AVLNode<T>* parent){// 调整节点位置及父子关系AVLNode<T>* cur = parent->_right;AVLNode<T>* lchild = cur->_left;parent->_right = lchild;if (lchild != nullptr)lchild->_parent = parent;cur->_left = parent;// 进行旋转AVLNode<T>* super = parent->_parent;cur->_parent = super;parent->_parent = cur;AVLNode<T>*& port = super == nullptr ? _root : (super->_left == parent ? super->_left : super->_right);port = cur;// 调节平衡因子cur->_bf = 0;parent->_bf = 0;}// 左右双旋void rotateLR(AVLNode<T>* parent){// 先把里面的节点旋出来，再按照单旋转处理AVLNode<T>* cur = parent->_left;AVLNode<T>* sub = cur->_right;int bf = sub->_bf;rotateRR(cur);rotateLL(parent);// 调整平衡因子if (bf == 1)cur->_bf = -1;else if (bf == -1)parent->_bf = 1;}// 右左双旋void rotateRL(AVLNode<T>* parent){// 先把里面的节点旋出来，再按照单旋转处理AVLNode<T>* cur = parent->_right;AVLNode<T>* sub = cur->_left;int bf = sub->_bf;rotateLL(cur);rotateRR(parent);// 调整平衡因子if (bf == 1)parent->_bf = -1;else if (bf == -1)cur->_bf = 1;}
};