【刚体姿态运动学】角速度和欧拉角速率的换算关系的详细推导

0 引言

本文以一种新的角度推导刚体姿态运动学，也即角速度和欧拉角速率之间的换算，不同于相似博文的地方在于，本文旨在从原理上给出直观清晰生动的解释。将详细过程记录于此，便于后续学习科研查找需要。

1 符号

符号	含义
${E\}$	地面坐标系（惯性坐标系，牛顿运动定律严格成立）
${B\}$	随体坐标系（固连在刚体上，且原点位于质心）
$\Phi=[\phi,\theta,\psi]^T$	姿态角，ZYX欧拉角，分别为roll, pitch, yaw
$R_X(\phi),R_Y(\theta),R_z(\psi)$	随体坐标系绕地面坐标系X/Y/Z轴旋转 $\phi/\theta/\psi$ 角度得到的旋转矩阵
$^E_BR$	旋转矩阵，随体坐标系姿态在地面坐标系下的表达
$c, s$	$c$ 表示 $cos$ ， $s$ 表示 $s in$
${\omega_b}=[{\omega_{bx}},{\omega_{by}},{\omega_{bz}}]^T$	刚体相对地面坐标系转动的角速度在 ${B\}$ 系下的表达

2 欧拉角与旋转矩阵

这里我们使用ZYX欧拉角来表达姿态，那么有：
$\begin{equation} \begin{split} ^E_BR&=R_Z(\psi)R_Y(\theta)R_X(\phi)\\ &= \begin{bmatrix} c\psi & -s\psi & 0\\ s\psi & c\psi & 0\\ 0&0&1 \end{bmatrix} \begin{bmatrix} c\theta & 0 & s\theta\\ 0 & 1 & 0\\ -s\theta&0&c\theta \end{bmatrix} \begin{bmatrix} 1 & 0 & 0\\ 0 & c\phi & -s\phi \\ 0 & s\phi &c\phi \end{bmatrix}\\ &=\begin{bmatrix} c\psi c\theta & s\theta s\phi c\psi-c\phi s\psi & s\theta c\phi c\psi + s\psi s\phi\\ s\psi c\theta & s\theta s\phi s\psi+c\phi c\psi & s\theta c\phi s\psi - c\psi s\phi\\ -s\theta & c\theta s\phi & c\theta c\phi \end{bmatrix} \end{split} \end{equation}$
上述旋转矩阵用欧拉角给出，可以理解为：随体坐标系（1）先绕自身的 $\hat Z_B$ 轴旋转 $\psi$ 角度，（2）再绕 $\hat Y_B$ 轴旋转 $\theta$ 角度，（3）最后绕 $\hat X_B$ 轴旋转 $\phi$ 角度。

欧拉角和固定角的区别为：

欧拉角：刚体绕运动轴旋转的角度（内旋Intrinsic rotations）
固定角：刚体绕固定轴旋转的角度（外旋 Extrinsic rotations）

3 机体下的角速度表达与欧拉角的关系

姿态角速率 $\dot \Phi$ 和机体角速度 $\omega_b$ 之间的转换关系为：
在这里插入图片描述

该公式不便于记忆，但是需要知道如何推导，并且最重要的是理解其原理，关键的时候查找即可。我几乎把高赞和高收藏的博客都看了一遍，但是都没能理解作者的意思，写的也有一定模糊性，后来还是自己琢磨才明白的，于是将自己能够理解的推导过程记录如下。

4 推导

假设当前姿态角为 $\Phi=[\phi,\theta,\psi]^T$ ，为了使角速度的表达更直观，这里用 ${\omega_b}=[{\omega_{bx}},{\omega_{by}},{\omega_{bz}}]^T$ 代替上图所示的 ${\omega_b}=[p,q,r]^T$ ，那么:
由偏航角速率 $\dot \psi$ 引起的角速度在最终的 ${B\}$ 系下可以表达为：
$\begin{bmatrix}\omega_{bx}\\ \omega_{by}\\ \omega_{bz}\end{bmatrix}_{\dot\psi}= {^{B_{z,y,x}}_{B_{z}}R}\begin{bmatrix}0\\0\\\dot\psi\end{bmatrix}$
其中，
$\begin{split} ^{B_{z,y,x}}_{B_{z}}R&=R^T_X(\phi)R^T_Y(\theta)\\ {{^{B_{z,y,x}}_{B_{z,y}}}R}&=R^T_X(\phi)\\ {{^{B_{z,y}}_{B_{z}}}R}&=R^T_Y(\theta)\\ \end{split}$
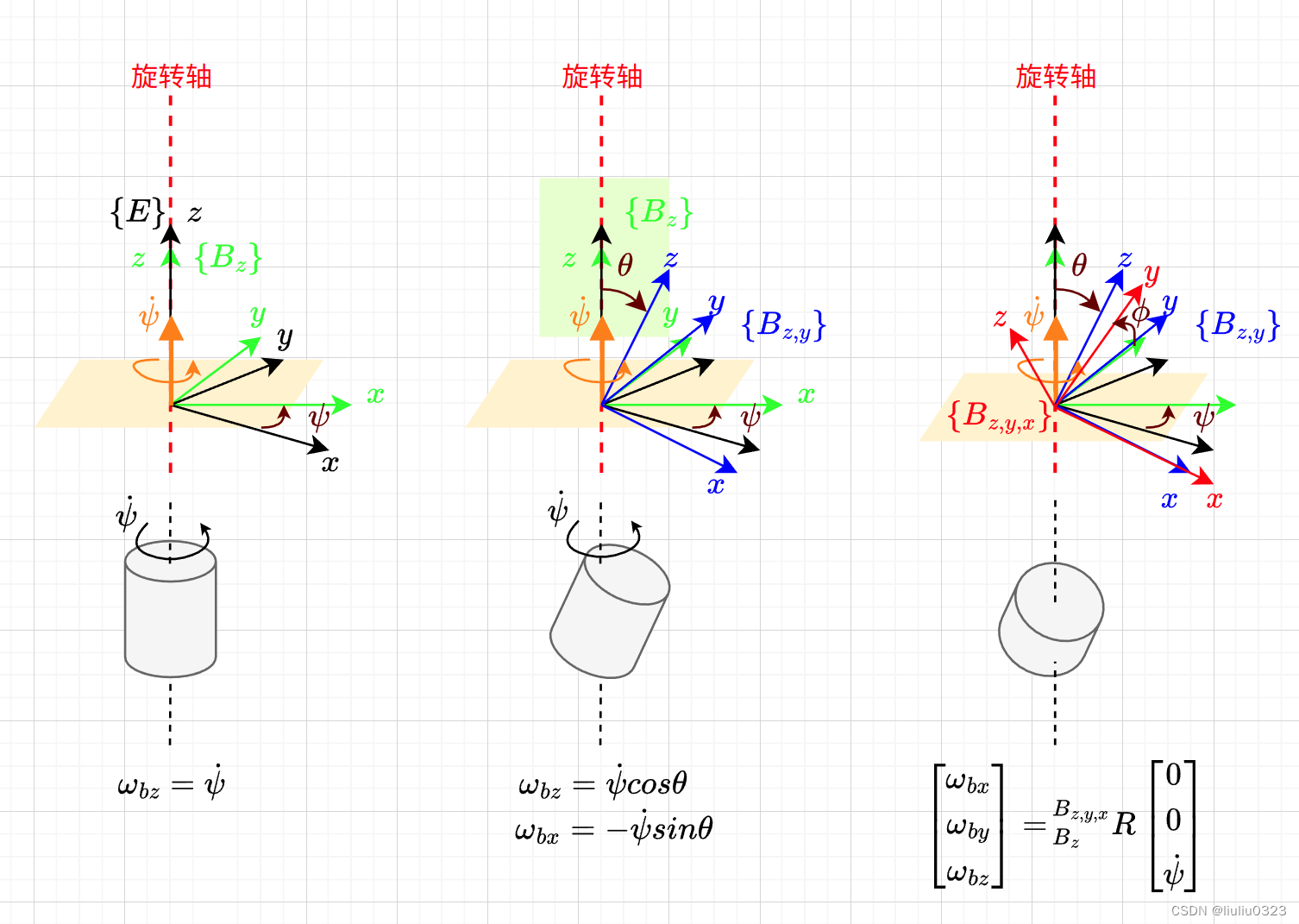
在这里插入图片描述
为了便于理解，我特地画了一个示意图，如上图所示。
这里假设物体有一个预设的姿态角（本文与其他文章最大的不同）：

第一幅图只有绕绿色 $z$ 轴的 $\psi$ 运动，为了与后面的情况作区分，这里 ${B_z\}$ 用下标 $_z$ 表示第一步绕机体 $z$ 轴的运动时的随体坐标系， $\omega_{bz}=\dot \psi$ 。
第二幅图，在第一幅图的基础上，俯仰角 $\theta$ 不为0，虽然引入了 $\theta$ ，但是却没有绕 $y$ 轴的运动，也即此时仍然只有 $\psi$ 变化，请大家想象第二幅图下方的圆柱，在倾斜的情况下，仍然绕“竖直”方向转动，那么显然，在这个时候的随体坐标系 ${B_{z,y}\}$ 下，出现了角速度的 $x$ 轴分量，而不仅仅有 $z$ 轴分量，也即角速度（注意橙色的 $\dot\phi$ 箭头）在新的坐标系下的表达。
同理，第三幅图，引入了 $\phi$ 角，但没有绕 $x$ 轴的运动（ $\dot \phi=0$ ），此时的机体角速度就是 $\dot \psi$ 角速度（注意橙色的 $\dot\phi$ 箭头）在姿态角 $\Phi$ 表示的坐标系下的表达。

类似的，如果 $\dot \theta$ 不为0，则由俯仰角速率 $\dot \theta$ 引起的角速度在最终的 ${B\}$ 系下可以表达为：
$\begin{bmatrix}\omega_{bx}\\ \omega_{by}\\ \omega_{bz}\end{bmatrix}_{\dot\theta}= {^{B_{z,y,x}}_{B_{z,y}}R}\begin{bmatrix}0\\\dot\theta\\0\end{bmatrix}$

由滚转角速率 $\dot \phi$ 引起的角速度在最终的 ${B\}$ 系下就更直接了，就是：
$\begin{bmatrix}\omega_{bx}\\ \omega_{by}\\ \omega_{bz}\end{bmatrix}_{\dot\phi}= \begin{bmatrix}\dot\phi\\0\\0\end{bmatrix}$

以上三个成分相加：
$\begin{split} \begin{bmatrix}\omega_{bx}\\ \omega_{by}\\ \omega_{bz}\end{bmatrix}&= \begin{bmatrix}\omega_{bx}\\ \omega_{by}\\ \omega_{bz}\end{bmatrix}_{\dot\psi}+\begin{bmatrix}\omega_{bx}\\ \omega_{by}\\ \omega_{bz}\end{bmatrix}_{\dot\theta}+\begin{bmatrix}\omega_{bx}\\ \omega_{by}\\ \omega_{bz}\end{bmatrix}_{\dot\phi}\\ &= R^T_X(\phi)R^T_Y(\theta)\begin{bmatrix}0\\0\\\dot\psi\end{bmatrix} +R^T_X(\phi)\begin{bmatrix}0\\\dot \theta\\0\end{bmatrix} +\begin{bmatrix}\dot\phi\\0\\0\end{bmatrix}\\ &= \begin{bmatrix} c\theta & 0 & -s\theta\\ s\theta s\phi & c\phi & c\theta s\phi \\ s\theta c\phi & -s\phi & c\theta c\phi \end{bmatrix} \begin{bmatrix}0\\0\\\dot\psi\end{bmatrix} + \begin{bmatrix} 1 & 0 & 0\\ 0 & c\phi & s\phi\\ 0 & -s\phi & c\phi \end{bmatrix} \begin{bmatrix}0\\\dot \theta\\0\end{bmatrix} +\begin{bmatrix}1&0&0\\0&1&0\\0&0&1\end{bmatrix} \begin{bmatrix}\dot\phi\\0\\0\end{bmatrix}\\ &= \begin{bmatrix} 1& 0& -s\theta \\ 0& c\phi& c\theta s\phi \\ 0&-s\phi& c\theta c\phi \end{bmatrix} \begin{bmatrix} \dot\phi\\\dot\theta\\\dot\psi \end{bmatrix} \end{split}$
也即：
$\begin{bmatrix}\omega_{bx}\\ \omega_{by}\\ \omega_{bz}\end{bmatrix}= \begin{bmatrix} 1& 0& -\text{sin}\theta \\ 0& \text{cos}\phi& \text{cos}\theta \text{sin}\phi \\ 0&-\text{sin}\phi& \text{cos}\theta \text{cos}\phi \end{bmatrix} \begin{bmatrix} \dot\phi\\\dot\theta\\\dot\psi \end{bmatrix}$
上述矩阵的逆，由matlab代码求出：

syms theta phi real
A=[1,0,-sin(theta);0,cos(phi),cos(theta)*sin(phi);0,-sin(phi),cos(theta)*cos(phi)];
A_inv = simplify(inv(A))

在这里插入图片描述
也即：
$\begin{bmatrix} \dot\phi\\\dot\theta\\\dot\psi \end{bmatrix}= \begin{bmatrix} 1 & \text{sin}\phi \text{tan}\theta & \text{cos}\phi \text{tan}\theta\\ 0 & \text{cos}\phi & -\text{sin}\phi \\ 0 & \text{sin}\phi/\text{cos}\theta & \text{cos}\phi/\text{cos}\theta \end{bmatrix} \begin{bmatrix}\omega_{bx}\\ \omega_{by}\\ \omega_{bz}\end{bmatrix}$