NC65 斐波那契数列

题目描述：

分析：
使用递归求解，当输入参数等于1、2时返回整数1

class Solution {
public:int Fibonacci(int n) {if(n == 1 || n == 2){return 1;}return Fibonacci(n-1) + Fibonacci(n-2);}
};

NC103 反转字符串

题目描述：

分析：
使用string迭代器逆向打印存入字符串返回

#include<string>
class Solution {
public:string solve(string str) {string s;string::reverse_iterator rit = str.rbegin();while(rit != str.rend()){s.push_back(*rit);++rit;}return s;}
};

NC141 判断是否为回文字符串

题目描述：

分析：
先找到首字符strat和最后一个字符end的位置
然后进行比较，如果不相等直接返回false
如果相等，则++start，–end
当start大于等于end时，则正常结束，跳出循环，返回true

class Solution {
public:bool judge(string str) {//首字符索引char start = 0;//最后一个字符索引char end = str.size()-1;while(start < end){if(str[start] != str[end]){return false;}++start;--end;}return true;}
};

NC151 最大公约数

题目描述：

分析：
定义一个变量tmp用来存储a，b中较小的数。
然后用a，b对tmp进行取余，如果有余数，则对tmp进行–操作。
直到被a，b两数整除则为a，b的最大公约数。返回该值。

class Solution {
public:int gcd(int a, int b) {int tmp = (a>b)? b:a;while(tmp){if(a%tmp == 0 && b%tmp == 0){return tmp;}--tmp;}return 1;}
};

NC4 判断链表中是否有环

题目描述：

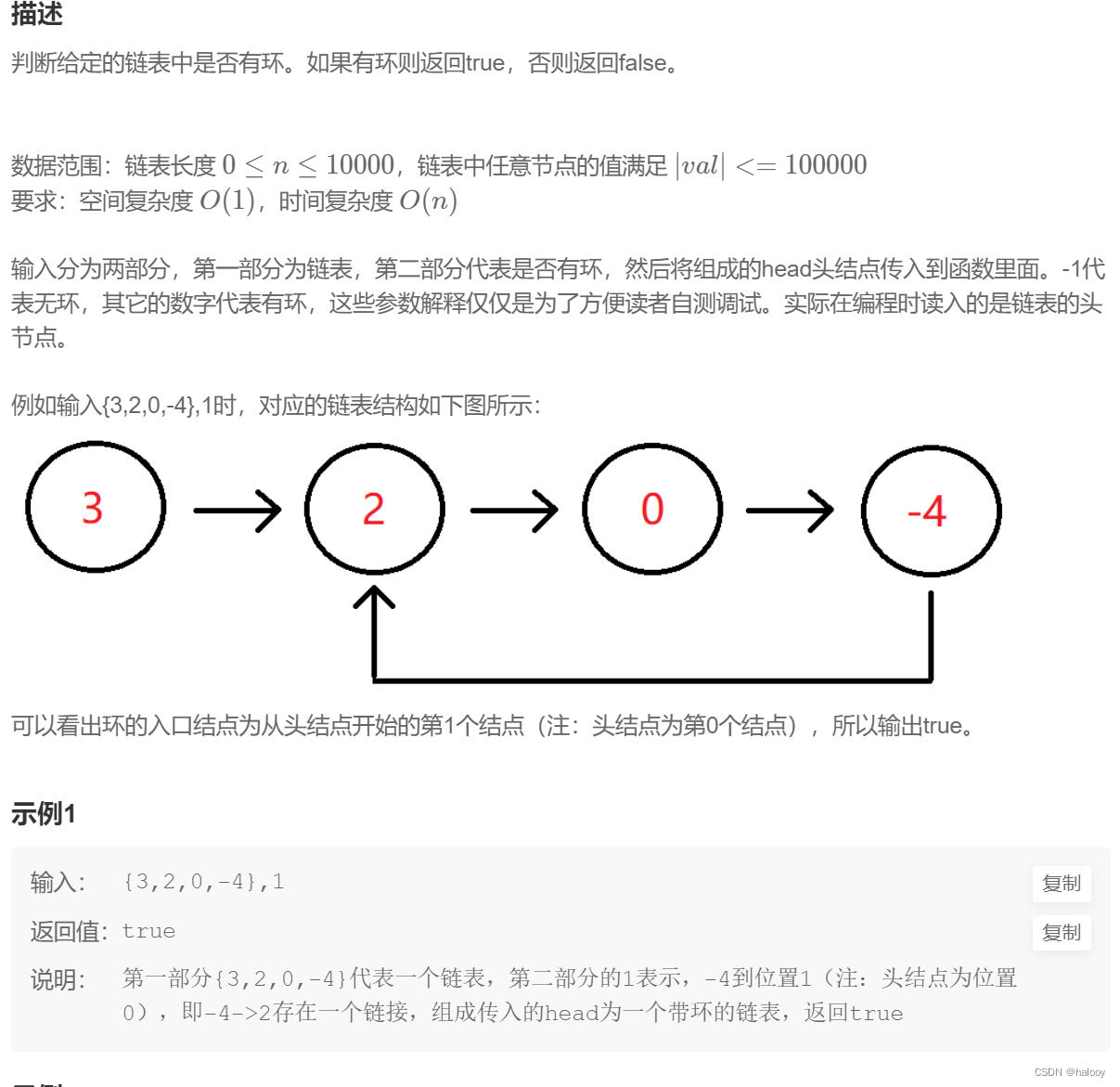
分析：
定义两个指针一开始都指向头节点，区别在于步长不同，一快一慢。
slow 指针每次向后移动一个位置，而fast 指针向后移动两个位置。如果链表中存在环，则 fast 指针最终将再次与 slow 指针在环中相遇。
如果不存在环，则fast指针会指向nullptr，则返回false

/*** Definition for singly-linked list.* struct ListNode {*     int val;*     ListNode *next;*     ListNode(int x) : val(x), next(NULL) {}* };*/
class Solution {public:bool hasCycle(ListNode* head) {if (head == nullptr) {return false;} else {ListNode* fast;ListNode* slow;fast = slow = head;while (fast != nullptr && fast->next != nullptr) {fast = fast->next->next;slow = slow->next;if(fast == slow){return true;}}return false;}}
};

NC7 买卖股票的最好时机(一)

题目描述：

分析1（动态规划）：

思路：对于每一天都有两个状态：到此为止的最大收益和是否持股。
因此用：
dp[i][0]表示第i天不持股到该天为止的最大收益，
dp[i][1]表示第i天持股，到该天为止的最大收益。
然后对于之后的每一天，都根据前一天的情况进行赋值。
如果当天不持股，有可能是前面的若干天中卖掉了或是还没买，因此到此为止的总收益和前一天相同，也有可能是当天才卖掉；
如果当天持股，有可能是前面若干天中买了股票，当天还没卖，因此收益与前一天相同，也有可能是当天买入，此时收益为负的股价。

class Solution {
public:int maxProfit(vector<int>& prices) {int n = prices.size();vector<vector<int>> dp(n, vector<int>(2, 0));//第一天不持股收益dp[0][0] = 0;//第一天持股收益dp[0][1] = -prices[0];for(int i = 1; i < n; ++i){//第i天不持股最大收益：//1.前一天也不持股，前几天卖掉或者没买，收益和前一天相同//2.前一天持股，第i天当天抛出，收益为前一天持股加上当天抛出dp[i][0] = max(dp[i-1][0], dp[i-1][1] + prices[i]);//第i天持股最大收益：//1.前一天不持股，第i天当天买入，收益为当天买入价格的负数//2.前一天持股，收益和前一天相同dp[i][1] = max(-prices[i], dp[i-1][1]);}//最后一天不持股，到改天为止的最大收益return dp[n-1][0];}
};

分析2(贪心思想):
思路：如果在某一天卖出了股票，那么要想收益最高，一定是它前面价格最低的那天买入的股票才可以。因此可以利用贪心思想解决，每次都将每日收入与最低价格相减维护最大值。
将第一天看成价格最低，后续遍历的时候遇到价格更低则更新价格最低。
每次都比较最大收益与当日价格减去价格最低的值，选取最大值作为最大收益。

class Solution {
public:/*** 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可** * @param prices int整型vector * @return int整型*/int maxProfit(vector<int>& prices) {// write code hereint n = prices.size();if(n == 0)return 0;//最大收益int maxProfit;//当天最大收益int max_td;//截至当天最低价格，将第一天看作价格最低int lessPrice = prices[0];//买入必须是卖出前一天maxProfit = 0;for(int i = 1; i < n; ++i){//第i天的最大收益，当天价格减去先前最低价格max_td = prices[i]-lessPrice;//如果第i天的最大收益比之前的大，则更新最大收益maxProfit = max(maxProfit, max_td);//如果先前最低价格大于第i天的价格，则更新最低价格//由于买入必须是卖出前一天，因此先计算第i天的最大收益后再更新最低价格lessPrice = min(lessPrice, prices[i]);}return maxProfit;}
};