什么是跳跃表(skip list)
跳跃表(Skip List)是一种概率性的数据结构,它通过在多层链表的基础上添加“快速通道”来提高搜索效率。跳跃表的效率可以与平衡树相媲美,即在平均和最坏的情况下,查找和插入操作都可以在 O(logn) 的时间复杂度内完成,其中 n 是跳跃表中的元素数量。
跳跃表的工作原理:
- 多层链表:跳跃表包含多个层次,每个层次都是一个有序的链表。底层是完整的有序链表,包含所有的元素。每一层(除了底层)都是下面一层的一个“子集”,其中包含了选定的元素和指向这些元素的指针。
- 节点晋升:当在跳跃表中插入一个新元素时,这个元素首先被插入到底层链表中。然后,通过一种随机过程(例如抛硬币),决定这个元素是否“晋升”到上一层链表。这个过程可能会继续,导致元素可能会出现在多个层次中。
- 快速查找:查找元素时,从最高层开始,快速前进直到无法继续前进为止(因为下一个元素大于要查找的元素),然后下降到下一层继续查找。这样,可以跳过大量不需要的元素,从而加速查找过程。
为什么使用跳跃表?
跳跃表之所以有效,是因为它们利用了概率平衡来减少维护平衡所需的工作量,与平衡树相比,跳跃表在实现上更为简单,且不需要复杂的旋转操作。Redis选择使用跳跃表作为有序集合的一部分,是因为它们非常适合于实现范围查询和有序遍历,这些操作在有序集合中非常常见。
跳跃表与内存使用:
虽然跳跃表会使用多个层次来存储指向相同数据的指针,但由于这些指针指向的是相同的数据元素,所以元素的实际数据并不会被复制多份,因此并不会造成数据本身的重复存储。指针和层次结构是额外的开销,但这是为了获得在对数时间内执行搜索、插入和删除操作的能力。
举个例子:
1、多层链表:
想象一下,你有一串编号的盒子排成一行,每个盒子都代表一个元素,编号越大的盒子放在越后面。现在,如果你想找到特定编号的盒子,你可能需要从第一个盒子开始,一个接一个地查看,直到找到你要的盒子。
这就像跳跃表的底层链表:每个盒子都直接连接到下一个,你需要逐个检查。
现在,假设我们在这些盒子之上加了一层,这一层只包含一些选定的盒子,并且每个选中的盒子都有一个指针指向它在下一层的对应盒子。这些选中的盒子让你可以跳过那些没有被选中的盒子,因此如果你在上层找不到你要的盒子,你可以下降到底层继续寻找。
这相当于跳跃表的第二层,其中一些元素被“晋升”到了这一层。
继续这个过程,我们可以添加更多的层,每个层次比下面的层次包含更少的元素。在顶层,可能只有几个盒子。当你开始搜索时,你会从顶层开始,利用这些“快速通道”迅速逼近你的目标编号。一旦你在某一层上不能再接近目标了,你就下降到下一层继续搜索。这样,你可以快速跳过那些不相关的编号,直到找到你要的盒子。
在实际的跳跃表中,元素是否晋升到更高的层级是通过随机化过程决定的,这样可以保证结构的平衡,而不需要复杂的调整。
以下是一个形象的跳跃表示例:
层 3: 1 ------------------------------> 9层 2: 1 --------> 5 --------> 7 -------> 9层 1: 1 -> 3 -> 5 -> 6 -> 7 -> 8 -> 9- 底层(层 1)含有所有元素(盒子)。
- 第二层(层 2)含有编号为 1, 5, 7, 9 的盒子,可以跳过 3、6、8。
- 第三层(层 3)只含有编号为 1 和 9 的盒子,提供了从开始到结束的快速通道。
如果你想找编号为 7 的盒子,从层 3 开始,发现你需要下降到层 2,因为层 3 里没有编号为 7 的盒子。
在层 2,你从 5 直接跳到 7,省去了检查 3 和 6 的需要。
这样,你就高效地找到了目标。
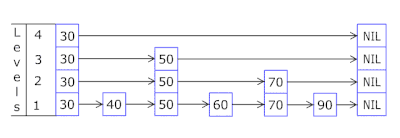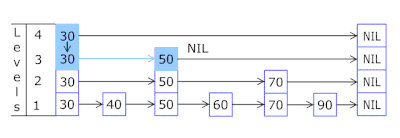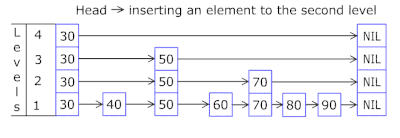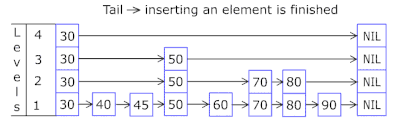
2、节点晋升
在跳跃表中,节点的晋升是通过随机化过程来实现的,以确保整个跳跃表的平衡。一个常见的方法是使用抛硬币的方式来决定一个节点是否晋升到上一层,这个方法称为“硬币翻转”(coin flipping)。
节点晋升过程的步骤如下:
- 插入节点:首先,新的节点被插入到跳跃表的最底层链表中。
- 抛硬币:然后,进行硬币翻转来决定这个节点是否晋升到上一层。硬币翻转是一个随机过程,通常是50%的概率来决定。
- 晋升节点:如果硬币翻转结果是正面(例如“头”),则节点晋升到下一个层级。
- 重复晋升:对晋升到新层级的节点再次进行硬币翻转,决定它是否继续晋升。这个过程重复进行,直到翻转结果为反面(例如“尾”)为止。
假设你正在插入一个新节点A,并且你已经将其插入到了底层链表中。现在,你开始进行硬币翻转:
- 第一次翻转:得到“头”,节点A晋升到第2层。
- 第二次翻转:再次得到“头”,节点A继续晋升到第3层。
- 第三次翻转:这次得到“尾”,晋升过程停止,节点A在第3层停留。
通过这个随机晋升的过程,跳跃表自然地形成了多层结构,顶层的节点数目会比底层少,这样就可以快速跳过大量的节点,提高搜索效率。
这个随机化的过程有助于跳跃表在没有任何调整的情况下保持平衡,因为晋升的过程并不依赖于具体的数值或插入的顺序,而是依赖于概率。这个过程保证了跳跃表的操作在平均情况下都是高效的。
需要深入了解点这里
-----------------------------------------------------------------我是分割线--------------------------------------------------------------
看完了觉得不错就点个赞或者评论下吧,感谢!!!
如果本文哪里有误随时可以提出了,收到会尽快更正的



引用 (讲解拿指针比较))






)


)
算法)




