1 问题

在离散数学“关系”这一章的学习过程中，学到偏序集中极大元、极小元、最大元和最小元的求解方法，于是提出能不能用python语言实现偏序集中极大元、极小元、最大元和最小元的求解？

2 方法

1. 判断偏序集中的极大元、极小元、最大元和最小元需要先确定集合中整出关系，然后根据整出关系绘制哈斯图，我们利用Python中的networkx库和matplotlib库来绘制集合的哈斯图。

2. 根据绘制的哈斯图进行极大元、极小元、最大元和最小元的判断。

通过实验、实践等证明提出的方法是有效的，是能够解决开头提出的问题。

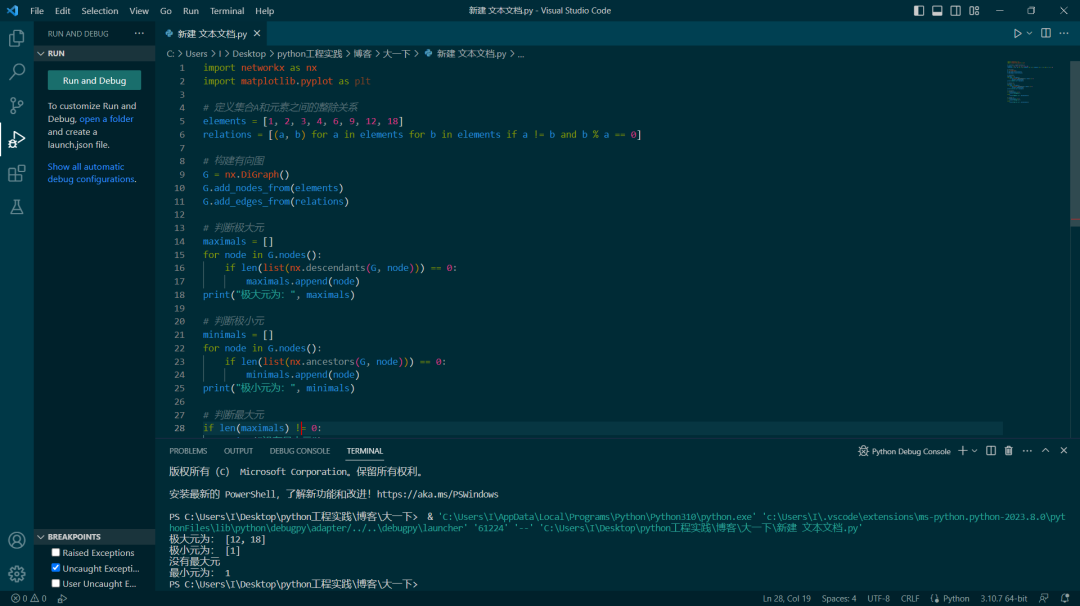
代码清单 1

import networkx as nx import matplotlib.pyplot as plt elements = [1, 2, 3, 4, 6, 9, 12, 18] relations = [(a, b) for a in elements for b in elements if a != b and b % a == 0] G = nx.DiGraph() G.add_nodes_from(elements) G.add_edges_from(relations) maximals = [] for node in G.nodes():    if len(list(nx.descendants(G, node))) == 0:        maximals.append(node) print("极大元为：", maximals) minimals = [] for node in G.nodes():    if len(list(nx.ancestors(G, node))) == 0:        minimals.append(node) print("极小元为：", minimals) if len(maximals) != 0:    print("没有最大元") else:    print("最大元为：", max(maximals)) if len(minimals) == 0:    print("没有最小元") else:    print("最小元为：", min(minimals))

3 结语

针对能不能用python语言实现偏序集中极大元、极小元、最大元和最小元的求解的问题，提出用Python中的networkx库和matplotlib库来绘制集合的哈斯图，然后通过哈斯图对极大元、极小元、最大元和最小元进行判断方法。通过实验，证明该方法是有效的。其中对于networkx库和matplotlib库的功能还不够了解，只知道库的少数功能的用法，对于其他的功能用法还不够熟练。但是随着学习的推进，我们一定能熟知并能灵活运用库的更多功能，完成其他更加复杂的工作。