数据结构-邻接表广度优先搜索(C语言版)

对于一个有向图无向图，我们下面介绍第二种遍历方式。

广度优先搜索，即优先对同一层的顶点进行遍历。

如下图所示：

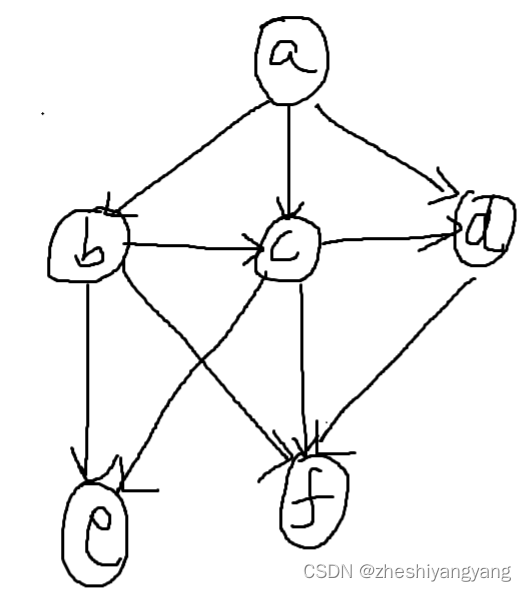
该例子，我们有六个顶点，十条边。

对于广度优先搜索，我们先搜索a，再搜索abcd，最后搜索ef。

而对于广度优先搜索，我们需要一个队列来辅助我们进行广度优先搜索（先进先出）。

同时我们还需要一个visit数组来判断某个顶点是否已经被搜索过了。

#include<stdio.h>#define MAX_NUM 100
typedef struct ArcNode{				//边 int adjvex;struct ArcNode *next;int weight;
}ArcNode;		typedef struct{						//头结点 char vertex;ArcNode *firstarc;
}VNode;typedef VNode Adjlist[MAX_NUM];			//邻接表 typedef struct{			//建立邻接表 Adjlist adjlist;int vexnum,arcnum;
}ALGraph;void DFSTraverse(ALGraph *G)		//深度优先搜索 
{int v;int visit[G->vexnum];for(v=0;v<G->vexnum;v++){visit[v] = 0;}for(v=0;v<G->vexnum;v++){if(visit[v]==0)DFS(G,v,visit);}
}void DFS(ALGraph *G,int v,int *visit)		//深度优先搜索后继结点判断 
{int w;ArcNode *p;printf("访问顶点:%c\n",G->adjlist[v].vertex);visit[v] = 1;p = G->adjlist[v].firstarc;while(p){w = p->adjvex;if(visit[w]==0)DFS(G,w,visit);p = p->next;}
}void BFSTraverse(ALGraph *G)		//广度优先搜索后继节点判断 
{int v,w,u;int Q[G->vexnum+1],r,f;int visit[G->vexnum];for(v=0;v<G->vexnum;v++)visit[v] = 0;f = 0,r = 0;for(v=0;v<G->vexnum;v++){if(visit[v]==0){visit[v] = 1;printf("第%d个结点是->%c\n",v,G->adjlist[v].vertex);Q[r] = v;r = (r+1)%(G->vexnum+1);while(f!=r){u = Q[f];f = (f+1)%(G->vexnum+1);ArcNode *p = G->adjlist[u].firstarc;while(p){if(visit[p->adjvex]==0){visit[p->adjvex] = 1;printf("第%d个结点是->%c\n",p->adjvex,G->adjlist[p->adjvex].vertex);Q[r] = p->adjvex;r = (r+1)%(G->vexnum+1);}p = p->next;}}}}
}int main()
{return 0;
}

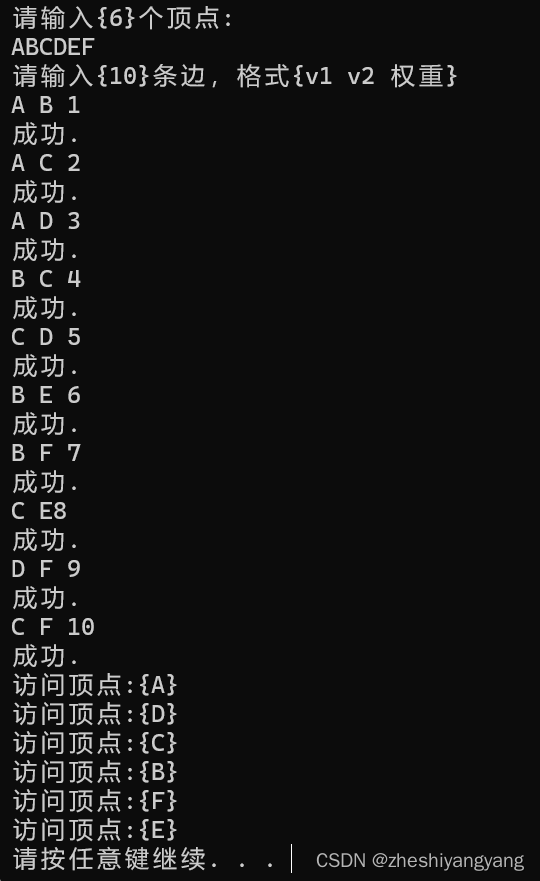
运行结果如下：