目录
1、数据分析
2、pytorch直线拟合
1、数据分析
直线拟合的前提条件通常包括以下几点:
存在线性关系:这是进行直线拟合的基础,数据点之间应该存在一种线性关系,即数据的分布可以用直线来近似描述。这种线性关系可以是数据点在直角坐标系上的分布趋势,也可以是通过实验或观测得到的数据点之间的关系。
数据点之间的误差是随机的:误差应该是随机的,没有任何系统性的偏差,并且符合随机误差的统计规律。这意味着数据点在拟合直线周围的分布应该是随机的,而不是受到某种特定的规律或趋势的影响。
直线应符合数据点的总体趋势:在拟合直线时,应该尽可能地符合数据点的总体趋势,而不是被一些异常值所影响。如果存在一些异常值,它们不应该对拟合结果产生过大的影响。
数据点的数量应该足够多:在进行直线拟合时,需要足够多的数据点来保证拟合结果的准确性和可靠性。通常来说,数据点的数量应该足够多,以便涵盖各种情况,并且能够反映出数据的真实分布情况。
数据的观测或实验过程是可靠的:数据的观测或实验过程应该是可靠的,这意味着数据的测量值应该是准确的,并且没有受到某些特定因素的影响。如果数据的观测或实验过程存在偏差或误差,那么直线拟合的结果也可能受到影响。
从散点图看出,数据具有明显的线性关系,本例不过多讨论数据是满足直线拟合的其它条件。
import torch
import matplotlib.pyplot as plt
x=torch.Tensor([1.4,5,11,16,21])
y=torch.Tensor([14.4,29.6,62,85,113.4])
plt.scatter(x.numpy(),y.numpy())
plt.show()
2、pytorch直线拟合
基于梯度下降法实现直线拟合。训练过程实际上是一种批量梯度下降(Batch Gradient Descent),这是因为每次更新参数时都使用了所有的数据。另外,学习率 learning_rate 和训练轮数 epochs 是可以调整的超参数,对模型的训练效果有很大影响。
import torch
import matplotlib.pyplot as plt
def Produce_X(x):x0=torch.ones(x.numpy().size)X=torch.stack((x,x0),dim=1)return X
def train(epochs=1,learning_rate=0.01):for epoch in range(epochs):output=inputs.mv(w)loss=(output-target).pow(2).sum()loss.backward()w.data-=learning_rate*w.gradw.grad.zero_()if epoch%80==0:draw(output,loss)return w,loss
def draw(output,loss):plt.cla()plt.scatter(x.numpy(), y.numpy())plt.plot(x.numpy(),output.data.numpy(),'r-',lw=5)plt.text(5,20,'loss=%s' % (loss.item()),fontdict={'size':20,'color':'red'})plt.pause(0.005)
if __name__ == "__main__":x = torch.Tensor([1.4, 5, 11, 16, 21])y = torch.Tensor([14.4, 29.6, 62, 85.5, 113.4])X = Produce_X(x)inputs = Xtarget = yw = torch.rand(2, requires_grad=True)w,loss=train(10000,learning_rate=1e-4)print("final loss:",loss.item())print("weigths:",w.data)plt.show()
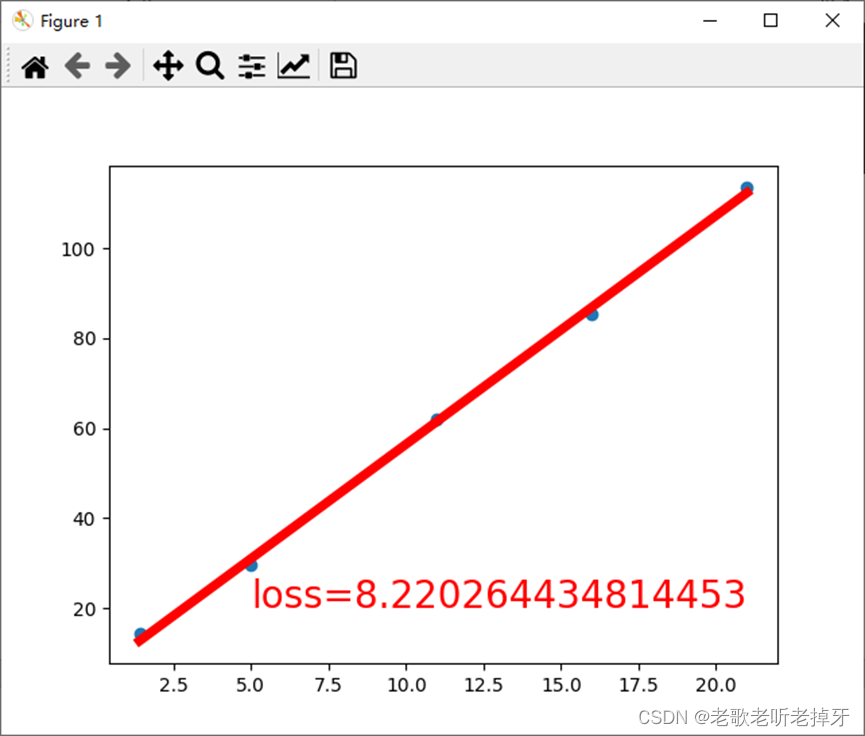
final loss: 8.216197967529297
weigths: tensor([5.0817, 5.6201])