题目链接

[NOIP2000 提高组] 方格取数

题目描述

设有 $N\times N$ 的方格图 $(N\le 9)$，我们将其中的某些方格中填入正整数，而其他的方格中则放入数字 $0$。如下图所示（见样例）:

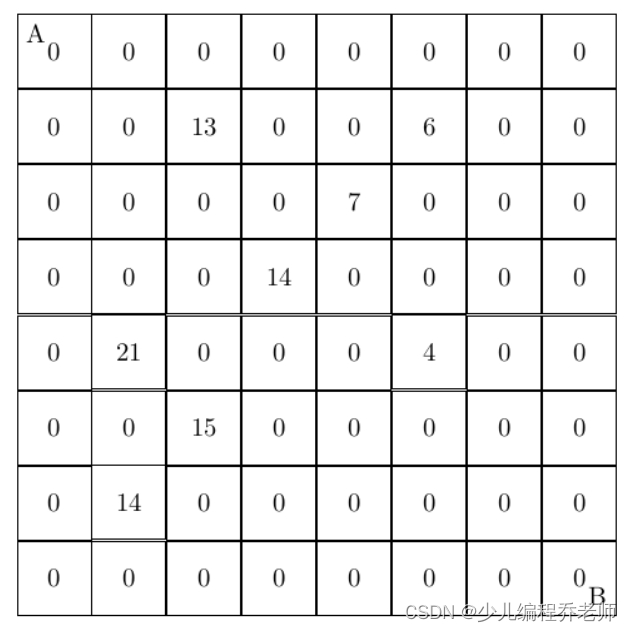
某人从图的左上角的 $A$ 点出发，可以向下行走，也可以向右走，直到到达右下角的 $B$ 点。在走过的路上，他可以取走方格中的数（取走后的方格中将变为数字 $0$）。
此人从 $A$ 点到 $B$ 点共走两次，试找出 $2$ 条这样的路径，使得取得的数之和为最大。

输入格式

输入的第一行为一个整数 $N$（表示 $N\times N$ 的方格图），接下来的每行有三个整数，前两个表示位置，第三个数为该位置上所放的数。一行单独的 $0$ 表示输入结束。

输出格式

只需输出一个整数，表示 $2$ 条路径上取得的最大的和。

样例 #1

样例输入 #1

8
2 3 13
2 6  6
3 5  7
4 4 14
5 2 21
5 6  4
6 3 15
7 2 14
0 0  0

样例输出 #1

67

算法思想（动态规划）

算法思想（动态规划）

根据题目描述，要求从$(1,1)$到$(n,n)$共走两次，试找出 $2$ 条这样的路径，使得取得的数之和为最大。

在取数过程中，由于每个格子只能取数一次。那么存在这样的性质：除了起点和终点，当路径没有交点时，收益不会比存在交点时更差。证明方式参考博主的另一篇博客：NOIP2005提高组第二轮T3：传纸条。

有了上述性质，就可以让两个条路径同时从左上角的 $A$ 点出发，每次同时走一步，由于只能向下和向右走，最终会同时到达右下角。那么可以用下述动态规划思想来解决：

• 状态表示：f[x1,y1,x2,y2]表示两条路径同时走了若干步之后，第一条到达(x1, y1)、第二条到达(x2, y2)时的最大值。
• 状态计算，可以按照最后一步的走法分成下面$4$种情况，取其中的最大值：
  • 同时向右走为，f[x1,y1-1,x2,y2-1] + w[x1, y1] + w[x2, y2]
  • 第一条向右走、第二条向下走为，f[x1,y1-1,x2-1,y2] + w[x1, y1] + w[x2, y2]
  • 第一条向下走、第二条向右走为，f[x1-1,y1,x2,y2-1] + w[x1, y1] + w[x2, y2]
  • 同时向下走为，f[x1-1, y1,x2-1,y2]+ w[x1, y1] + w[x2, y2]

需要注意的是，在状态计算中：

• 两条路径如果走到相同格子，那么该格子的数字只能加$1$次

时间复杂度

一共有 $O(n^4)$ 个状态，每个状态需要 $O(1)$的计算量，因此总时间复杂度是 $O(n^4)$。

代码实现

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 15;
int w[N][N], f[N][N][N][N];int main()
{int n, x, y, z;cin >> n;while(cin >> x >> y >> z, x || y || z) w[x][y] = z;for(int x1 = 1; x1 <= n; x1 ++)for(int y1 = 1; y1 <= n; y1 ++)for(int x2 = 1; x2 <= n; x2 ++)for(int y2 = 1; y2 <= n; y2 ++){int t = max(max(f[x1][y1 - 1][x2][y2 - 1], f[x1][y1 - 1][x2 - 1][y2]),max(f[x1 - 1][y1][x2 - 1][y2], f[x1 - 1][y1][x2][y2 - 1]));if(x1 == x2 && y1 == y2)f[x1][y1][x2][y2] = t + w[x1][y1];else f[x1][y1][x2][y2] = t + w[x1][y1] + w[x2][y2]; }cout << f[n][n][n][n] << endl;
}