分类目录：《深入理解强化学习》总目录
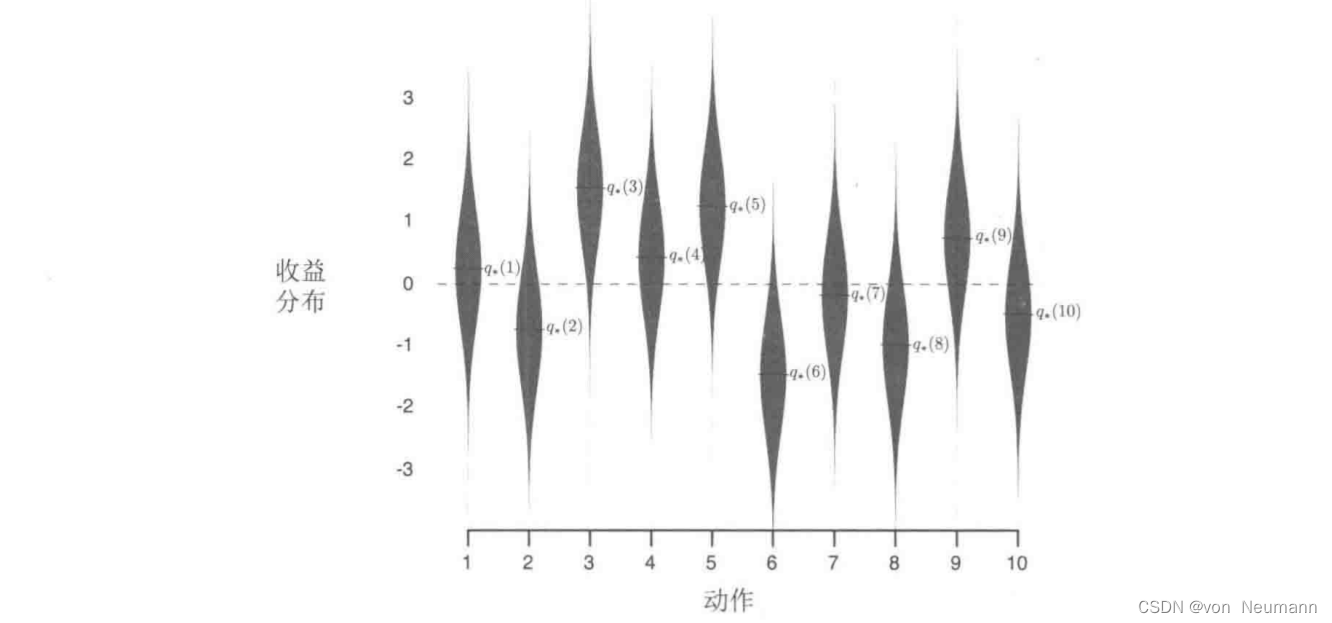
为了大致评估贪心方法和 ϵ − \epsilon- ϵ−贪心方法相对的有效性，我们将它们在一系列测试问题上进行了定量比较。这组问题是2000个随机生成的 k k k臂赌博机问题，且 k = 10 k=10 k=10。在每一个赌博机问题中，如下图显示的那样，动作的真实价值为 q ∗ ( a ) , a = 1 , 2 , ⋯ , 10 q_*(a), a=1, 2, \cdots, 10 q∗(a),a=1,2,⋯,10，从一个均值为 0 0 0方差为 1 1 1的标准正态（高斯）分布中选择。当对应于该问题的学习方法在 t t t时刻选择 A t A_t At时，实际的收益 R t R_t Rt则由一个均值为 q ∗ ( A t ) q_*(A_t) q∗(At)方差为 1 1 1的正态分布决定。在下图中，这些分布显示为灰色区域。我们将这一系列测试任务称为10臂测试平台。对于任何学习方法，随着它在与一个赌博机问题的1000时刻交互中经验的积累，我们可以评估它的性能和动作。这构成了一轮试验。用2000个不同的赌博机问题独立重复2000个轮次的试验，我们就得到了对这个学习算法的平均表现的评估。
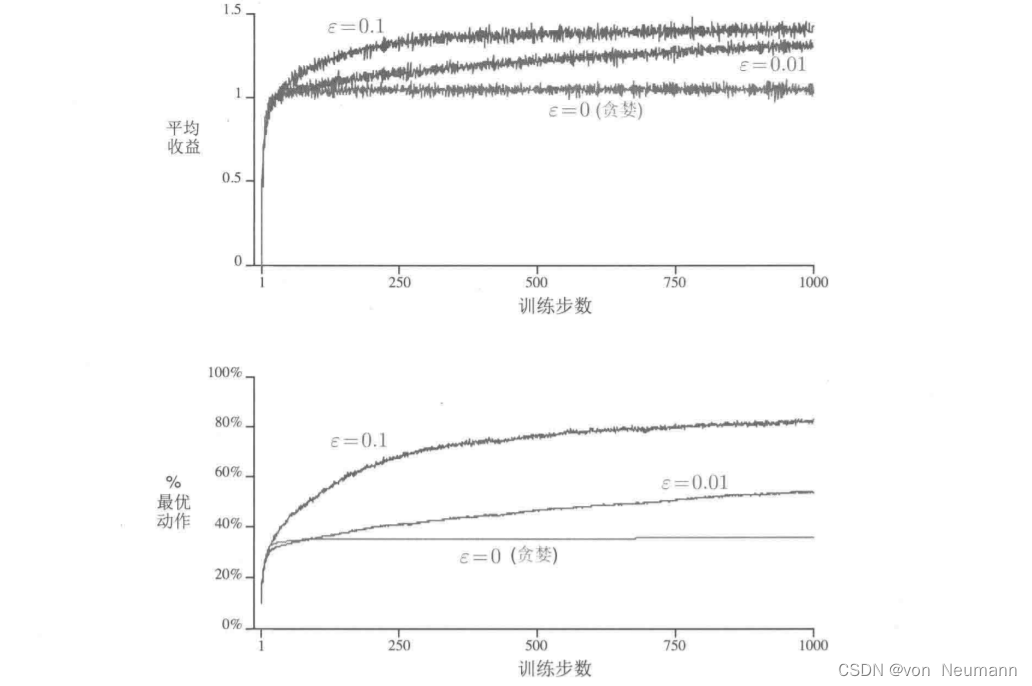
下图在一个10臂测试平台上比较了上述的贪心方法和两种 ϵ − \epsilon- ϵ−贪心方法（ ϵ = 0.01 \epsilon=0.01 ϵ=0.01和 ϵ = 0.1 \epsilon=0.1 ϵ=0.1）。所有方法都用采样平均策略来形成对动作价值的估计。上部的图显示了期望的收益随着经验的增长而增长。贪心方法在最初增长得略微快一些，但是随后稳定在一个较低的水平。相对于在这个测试平台上最好的可能收益 1.55 1.55 1.55，这个方法每时刻只获得了大约1的收益。从长远来看，贪心的方法表现明显更糟，因为它经常陷入执行次优的动作的怪圈。下部的图显示贪心方法只在大约三分之一的任务中找到最优的动作。在另外三分之二的动作中，最初采样得到的动作非常不好，贪心方法无法跳出来找到最优的动作。 ϵ − \epsilon- ϵ−贪心方法最终表现更好，因为它们持续地试探并且提升找到最优动作的机会。 ϵ = 0.1 \epsilon=0.1 ϵ=0.1的方法试探得更多，通常更早发现最优的动作，但是在每时刻选择这个最优动作的概率却永远不会超过91％（因为要在 ϵ = 0.1 \epsilon=0.1 ϵ=0.1的情况下试探）。 ϵ = 0.01 \epsilon=0.01 ϵ=0.01的方法改善得更慢，但是在图中的两种测度下，最终的性能表现都会比 ϵ = 0.1 \epsilon=0.1 ϵ=0.1的方法更好。为了充分利用高和低的 ϵ \epsilon ϵ值的优势，随着时刻的推移来逐步减小 ϵ \epsilon ϵ也是可以的。
ϵ − \epsilon- ϵ−贫心方法相对于贪心方法的优点依赖于任务。比方说，假设收益的方差更大，不是1而是10，由于收益的噪声更多，所以为了找到最优的动作需要更多次的试探，而 ϵ − \epsilon- ϵ−贪心方法会比贪心方法好很多。但是，如果收益的方差是0，那么贪心方法会在尝试一次之后就知道每一个动作的真实价值。在这种情况下，贪心方法实际上可能表现最好，因为它很快就会找到最佳的动作，然后再也不会进行试探。但是，即使在有确定性的情况下，如果我们弱化一些假设，对试探也有很大的好处。例如，假设赌博机任务是非平稳的，也就是说，动作的真实价值会随着时间而变化。在这种情况下，即使在有确定性的情况下，试探也是需要的，这是为了确认某个非贪心的动作不会变得比贪心动作更好。如我们将在接下来的几章中所见，非平稳性是强化学习中最常遇到的情况。即使每一个单独的子任务都是平稳而且确定的，学习者也会面临一系列像赌博机一样的决策任务，每个子任务的决策随着学习的推进会有所变化，这使得智能体的整体策略也会不断变化。强化学习需要在开发和试探中取得平衡。
参考文献：
[1] 张伟楠, 沈键, 俞勇. 动手学强化学习[M]. 人民邮电出版社, 2022.
[2] Richard S. Sutton, Andrew G. Barto. 强化学习（第2版）[M]. 电子工业出版社, 2019
[3] Maxim Lapan. 深度强化学习实践（原书第2版）[M]. 北京华章图文信息有限公司, 2021
[4] 王琦, 杨毅远, 江季. Easy RL：强化学习教程 [M]. 人民邮电出版社, 2022
时间复杂度通过位运算来判断两字符串是否有公共字符方法)
