318. 最大单词长度乘积

难度: 中等

来源: 每日一题 2023.11.06

给你一个字符串数组 words ，找出并返回 length(words[i]) * length(words[j]) 的最大值，并且这两个单词不含有公共字母。如果不存在这样的两个单词，返回 0 。

示例 1：

输入：words = ["abcw","baz","foo","bar","xtfn","abcdef"]
输出：16 
解释：这两个单词为 "abcw", "xtfn"。

示例 2：

输入：words = ["a","ab","abc","d","cd","bcd","abcd"]
输出：4 
解释：这两个单词为 "ab", "cd"。

示例 3：

输入：words = ["a","aa","aaa","aaaa"]
输出：0 
解释：不存在这样的两个单词。

提示：

2 <= words.length <= 1000
1 <= words[i].length <= 1000
words[i] 仅包含小写字母

class Solution {public int maxProduct(String[] words) {}
}

分析与题解

位运算 + HashMap

当看到这个题目的时候, 我在想如何这个题目是属于哪一类题目呢? 最后感觉没法进行归类, 那就只能进行模拟, 然后再模拟过程中进行优化了.

暴力方案的话, 我们就从头遍历, 首先查找出两个单词, 然后逐字比对. 利用这样几层遍历来解决该问题. 具体模拟代码如下所示.
```
for (int i = 0; i < words.length(); i++) {// 查找第一个单词...for(int j = i + 1; j < words.length(); j++) {// 查找第二个单词for(int i = 0; i < word1.length(); i++) {// 遍历第一个单词的所有字母...for(int i = 0; i < word.length(); i++) {// 遍历第二个单词的所有字母...}}}
}
```
这时候时间复杂度是多少呢? 结果是 O( $n^4$ ), 根本不用跑测试用例, 肯定就超时了.

那么, 我们该怎么优化呢? 首先外层的查找遍历过程基本上没法进行优化了, 那么我们只能优化比对过程的遍历. 这时候, 我觉得觉得要使用位运算来解决了, 当然了, 这算是自己的经验吧. 没接触过位运算的童鞋还是比较难想到的.

这里的思路和官方的思路基本是一致的, 我们首先创建一个 int整型数据 用来存储某个单词的26个字母的情况. 26个举例太多了, 假设我们只有4个字母 a b c d, 那么我们有如下的设定.

a = 1 << 1

b = 1 << 2

c = 1 << 3

d = 1 << 4

我们只需要使用 按位或 | 运算就能把某个字母的情况添加到结果中. 比如一个单词是 ccda, 那么会遍历这个单词, 生成如下的步骤.

result = result | (1 << "ccda".charAt(0))

result = result | (1 << "ccda".charAt(1))

result = result | (1 << "ccda".charAt(2))

result = result | (1 << "ccda".charAt(3))

最终 result 就是单词 ccda的字母情况, 结果如下图所示.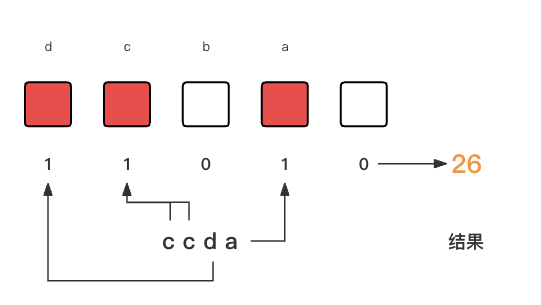

按照上面的这个思路的话, 我们可以得到每一个单词的字母情况, 并且为了方便下一步查找, 我们把它们存储到一个字典中去.
```
// 组装, 其中key是单词, value是二进制数, 表示单词都含有哪些字母
Map<String, Integer> cache = new HashMap<String, Integer>();
for(String word : words) {if (cache.get(word) == null) {int value = 0;for(int i = 0; i < word.length(); i++) {char singleWord = word.charAt(i);value = value | (1 << (singleWord - 'a' + 1));}cache.put(word, value);}
}  
```
那么, 我们该如何判断两个单词没有重复字母呢? 我们只需要通过 按位与& 对任意两个单词生成的字母情况整型数进行计算, 如果结果等于0, 那就说明没有重复位. 没有重复位也就说没有重复字母, 符合题意. 逻辑代码如下所示.
```
if ((cache.get(firstWord) & cache.get(secondeWord)) == 0) {result = Math.max(firstWord.length() * secondeWord.length(), result);
}
```
接下来, 我们就看一下整体的题解过程.
```
class Solution {public int maxProduct(String[] words) {// 组装, 其中key是单词, value是二进制数, 表示单词都含有哪些字母Map<String, Integer> cache = new HashMap<String, Integer>();for(String word : words) {if (cache.get(word) == null) {int value = 0;for(int i = 0; i < word.length(); i++) {char singleWord = word.charAt(i);value = value | (1 << (singleWord - 'a' + 1));}cache.put(word, value);}}int result = 0;for (int i = words.length - 1; i >= 0; i--) {String firstWord = words[i];for(int j = i - 1; j >= 0; j--) {String secondeWord = words[j];if ((cache.get(firstWord) & cache.get(secondeWord)) == 0) {result = Math.max(firstWord.length() * secondeWord.length(), result);}}}return result;}
}
```
复杂度分析:
- 时间复杂度: O(2n²), 两层的循环遍历的时间复杂度
- 空间复杂度: O(n), HashMap所需要的空间复杂度与单词数组成线性关系
结果如下所示.